Volume 10 Issue 1 pp. 72-86 • doi: 10.15627/jd.2023.6
Design Optimization of the Skylight for Daylighting and Energy Performance Using NSGA-II
Bahereh Vojdani Fakhr,⁎,a Mohammadjavad Mahdavinejad,a Morteza Rahbar,b Banafsheh Dabajc
Author affiliations
a Department of Architecture, Tarbiat Modares University, Tehran, Iran
b Computational Design & Digital Fabrication, Iran University of Science and Technology, Tehran, Iran
c Energy and Architecture, Pars University of Architecture and Art, Tehran, Iran
*Corresponding author.
Bahereh.vojdani@modares.ac.ir (B. Vojdani Fakhr)
mahdavinejad@modares.ac.ir (M. Mahdavinejad)
rahbarm@iust.ac.ir (M. Rahbar)
banafsheh.dabaj@pu.ac.ir (B. Dabaj)
History: Received 9 March 2023 | Revised 26 April 2023 | Accepted 29 April 2023 | Published online 23 May 2023
Copyright: © 2023 The Author(s). Published by solarlits.com. This is an open access article under the CC BY license (http://creativecommons.org/licenses/by/4.0/).
Citation: Bahereh Vojdani Fakhr, Mohammadjavad Mahdavinejad, Morteza Rahbar, Banafsheh Dabaj, Design Optimization of the Skylight for Daylighting and Energy Performance Using NSGA-II, Journal of Daylighting 10 (2023) 72-86. https://dx.doi.org/10.15627/jd.2023.6
Figures and tables
Abstract
In terms of sustainable design, lateral windows and skylights are important. Daylighting has become a vital component in office buildings because it increases occupants' productivity, well-being, and energy savings via windows and skylights. As a result, various factors have an impact on achieving Useful Daylight Illuminance (UDI) and lowering overheating and glare discomfort. First the merits of the skylight and the window are compared in this study. Second, this study constructs an intelligent optimization method NSGA-II based on Pareto front approaches that allows low energy use of the office building while maintaining excellent thermal and lighting comfort for the inhabitants. Finally, all optimum solutions look at Daylight Glare Probability (DGP) for visual comfort. Isfahan, Iran (32° N, 51° E) as a hot and dry climatic condition, is selected for the simulation. A variety of geometries with different parameters, were applied to meet the goal. Among the different cases, the optimization’s findings highlight the pyramidal design with the highest aperture on the floor. It's best for a hot, dry area and a space with a square or rectangular form. The degree of glare in all ideal geometries, on the other hand, was reasonable—furthermore, these findings aid designers in selecting the appropriate window for the building's form and environment.
Keywords
Multi-objective optimization, Skylight's geometry, Energy performance, Daylight
1. Introduction
Daylighting has been shown to have an impact on worker productivity, comfort, and well-being [1,2]. Architects and researchers are constantly challenged to achieve effective daylight control and reduce energy consumption by assessing thermal and visual comfort [3]. As a result, by effectively seizing daylight as a resource rather than relying on artificial light, proper daylighting may decrease energy waste [4,5]. The essence of sunlight inside a place varies according to several agents, including weather data, location, the direction of the building, building context, the hour, and season [6]. The skylight has become a common architectural feature in many building types due to its exceptional potential to bring daylight into the structure's center [7]. The impact of daylighting on human behavior is being studied more in the workplace and office, primarily in industrialized nations [8,9]. Regardless of light's color temperature, it was determined that light significantly impacts office operators and occupants [10,11]. Intelligent building optimization and energy loss minimization while maintaining occupant thermal and lighting comfort is critical [12].
Incoming direct solar radiation from the window may improve solar comfort within the building during the winter months while also lowering heating costs. However, in the summer, the opposite effect occurs since the sunlight distribution may create overheating and exacerbate the cooling state [13].
The primary disadvantage of a single glass window in designing a window system is that it cannot create adequate heat resistance and often results in significant cooling energy loss in the summer [14]. Architects use a large glass area to provide appreciating qualities and a broad perspective [15]. Some of them failed to account for visual and thermal comfort, as well as the quantity of energy used. Due to considerable solar gains in the summer, office buildings have very high cooling loads [16]. As a consequence, this research opts for an open workplace setting.
This study aims to figure out the best way to offer enough daylight for office workers while also lowering energy usage in a hot, dry region. The weather in this climatic zone is cold in the winter and scorching in the summer. As a result, this study demonstrates that the skylight takes precedence over the wall's window except for the outside view. On the other hand, controlling glare is difficult in a clear sky, and most of the time, it is managed by window shade [17]. However, the right skylight shape may help to alleviate visual discomfort [18].
This study focuses on the best skylight in a hot region to maximize useful sunshine illuminance while lowering the model's energy consumption without a lateral window in the wall. Furthermore, due to our instance's superb sunshiny climatic circumstances, the study achieves an extremely high degree of warming inside space, causing significant pain for inhabitants and wasting energy for cooling and lighting. We concentrate on the best design of the skylight in order to maximize energy savings and regulate the residents' interior thermal and visual comfort. This study uses a stochastic technique to handle this multi-objective optimization problem. The Pareto Front [18] is used to identify various optimum solutions for decision-makers to consider.
Many studies have been carried out related to skylight simulation in the terms of daylight efficiency [19], ventilation [20], energy consumption, thermal and visual comfort [21-23]. Some have concentrated on the skylight's single-objective optimization with the aim of minimizing energy consumption [24] and maximizing ventilation [25]. A number of studies have used the multi-objective genetic optimization approach to improve skylights aimed at daylight efficiency [26-28]. The significance of using the NSGA-II optimization method in the design of building envelopes [29], blinds [30], and louvers [31] can be seen in many studies. In contrast to previous studies that focused on improving skylight design for a specific goal, such as daylighting performance or energy efficiency, our research addresses a gap in the literature by providing a comprehensive and integrated approach using NSGA-II optimization method for enhancing skylight design that may balance several performance objectives such as maximizing useful daylight illuminance (UDI), thermal comfort, and energy performance, while minimizing glare discomfort. This method can aid architects in developing knowledgeable skylight designs that result in high-quality interior spaces while using less energy. The basic scenario's daylighting and energy modeling and analysis methodologies are explained separately in Section 3.
2. Literature review
Daylighting is an important aspect of environmental building design. Meanwhile, when correctly displayed, sunshine creates an aura of subtle design and aesthetic comfort, reducing the need for artificial lighting and environmental adjusting equipment [32]. As a result, the quality of internal lighting accessibility is determined by the structure's architecture. Structure massing and location, internal wall viewed identification, window layout in a building, and municipal planning influence daylight openness [33-37]. Several studies on skylights have been conducted in the past. However, most of them concentrate on basic forms [38-43]. Skylights are common in contemporary structures because they provide homogeneous illumination across the horizontal plane while allowing for daylight access in areas where there are no facades. The majority of scholars in this field have used classic daylighting procedures as their methodology [44]. As a result, there is a strong need to expand the research field to include different types of skylights and determine appropriate geometries.
However, increasing the height of proper daylighting can lead to excessive and uncomfortable levels of light. This presents a challenge in balancing the benefits of daylighting with the need to avoid discomfort. This challenge is particularly pronounced in buildings that rely on direct natural light from windows on the walls. Previous studies have highlighted the importance of configuration parameters in achieving this balance. Notably, while top-light apertures have been the focus of much research (as seen in references [45] and [46]), it is important to remember that these apertures work independently of side-light apertures. Daylighting a roof with skylights may result in significant energy savings [22,47].
By concentrating on the window's design and materials, several studies have attempted to reduce cooling and heating and discomfort hours [48,49]. Jing Zhao, for example, used the NSGA-II optimization algorithm to develop an easy-to-use, helpful, and valuable multi-objective optimization technique.
The skylight is installed over a hole in the building's roof. Individual roof lights, dome lights, ridge roof or curved continuous roof lights, and shed lights are only a few examples, and the glass may be on various sides of the direction [50]. Numerous studies have been conducted on daylight design, daylight performance, and glare reduction techniques. Although each study focused on a different topic, the overall goals were to improve visual comfort and reduce energy consumption or to use various methodologies to acquire studies that were essential in achieving these goals.
Daylighting is defined as the regulated admission of natural light, direct sunshine, and distributed skylight into a structure to reduce electric lighting; windows directly offer natural lighting for space [51]. Some studies looked at the efficacy of combining optimization techniques on window type and placement for energy efficiency, with a focus on aesthetic comfort [52]. Outstanding researchers have concentrated on building facades to reduce energy consumption and improve daylight efficiency [53,54]. Researchers investigated the impact of the skylight–roof ratio on daylight performance due to annual and daily fluctuations in solar circumstances and sky conditions. For example, in a warehouse design in the tropical zone, Remon Lapisa, M et al. investigated the influence of Skylight-to-roof ratios on energy efficiency for artificial lighting, daylight availability in the interior, and temperature discomfort [54]. Furthermore, Theodora Mavridou's study advocated determining the optimal distance between roof openings, which was made up of different roof compositions [55]. Some researchers have examined the impacts of skylights on occupants in various settings, including industrial buildings, malls, and even historical palaces, such as the Egyptian heritage palace skylight [19,56].
On the other hand, a few studies have looked into the impact of skylights in offices; Erica Cochran et al. looked into the office function and concentrated on dynamic shading on skylights [57]. Other researchers, such as Karam M et al., believe that skylights may assist reduce load and energy consumption in various structures. This hypothesis states that using this approach at the initial design stage will allow designers to successfully balance the architectural environment [58]. The importance of visual comfort has been emphasized in recent research [58-63]. Several studies have highlighted the significant variation in people's perceptions of uncomfortable glare [64-69]. Glare is described as the impression of brightness in a range of viewpoints that is too wide for the eye to adapt to. As a result, there has been pain and a loss of visibility [70].
2.1. Energy and daylight simulation
Based on the studies that have been reviewed in glare analysis, Daylight Glare Probability (DGP) is selected for evaluation in this study. Since Wienold and Christoffersen's discomfort glare formula for daylighting considers both the glare source and the brightness distribution of the sky, DGP may be a more accurate predictor of glare than other indices including Daylight Glare Index (DGI) [71]. The formula is described as Eq. (1) [71]
The investigation of interior daylight balance is often carried out using a way of modeling a genuine scenario with a collection of analytical formula measuring a range of metrics, such as Daylight Illuminance (DI), Daylight Coefficient (D.C.), and Daylight Autonomy (DA). Daylight autonomy (DA) is a proportion of the time spent using solely sunshine to achieve a certain user-specified lux threshold [72]. On the other hand, DA is usually expressed as a yearly figure, while it is possible to get annual, monthly, or regular results. DA's estimating approach specifies the illuminance values per hour for the whole year at a certain location. The illuminance range of 100 to 2000 lux is considered desirable. Extremely dark is defined as a place with less than 100 lux of lighting; similarly, extremely bright is defined as a space with more than 2000 lux of illumination. In this research, the UDI 100-2000 lux is indicated as UDI, and it is proven to be the most effective daylight criterion [73]. DA gives an intuitive sense of how well light will enter a space and allows the architect to calculate the corresponding electric energy savings with relative ease. The main disadvantage is that, since DA lacks an upper limit for daylight illuminance, it ignores issues related to visual comfort when exposed to intense sunshine [74]. Credit is provided if the level of illuminance exceeds a specified lux threshold and is applied to a specific time of application; it is a dynamic measure based on climatic data [75]. Spatial daylight autonomy (sDA) [76] is defined as the proportion of floor space with no less than 300 lux for at least 50% of the annual busy hours.
The investigation can only include the working area following the vision simulator, although the whole place is usually recognized. Imagine N points in a network, and indicate a function S.T. (i) whose amount fits unit for each point of the network, taking the lowest requisite illuminance for exceeding the assigned portion of the total amount of time an individual consumes in; the sDA is demonstrated in Eq. (2) [76]
where ST (i) indicates the incident number of passing the sDA illuminance start at point i, is the annual digital record of the time of occurrence of a particular event. The LEED ver.4 needs the consideration of architects to the Annual Sunlight Exposure (ASE) and sDA to score 2 to 3, sequentially by giving 55_75% of the filled space's area. To obtain this aim, architects adopting annual computer simulations must determine that the annual direct solar radiation of is obtained in fewer than 10% of the space. It is essential that simulation run based on
2.2. Multi-Objective optimization
A computer-based assessment of the amount of daylight accessible inside or outside a structure under one or more sky situations provides various profitable options among single and numerous environmental execution models. The building optimization approach provides a way out in identifying previously stated antagonistic goals, such as energy and daylight study. Zhai [49] employed NSGA-II in an optimization problem with various objective functions to optimize window-related design factors in the amount of energy or power consumed, comfort with the thermal environment, and visual comfort. The results were shown using a graphical representation of the Pareto Set, which described a multi-objective optimization problem. Cheong et al. [63] created internal environmental needs in a current workplace by using a horizontal surface that reflects sunshine deep into the space to maximize thermal and daylighting performance. A lighting sensor must be installed in the structure to control energy savings from daylight. The approach is connected to the simulation of building performance simulation. Once a year, a daylighting scheme is developed. The energy model entails keeping track of electric lights, maintaining suitable temperatures, and adjusting demand for daylighting. Marzouk et al. [77] and Yılmaz et al. [78] provides a comprehensive explanation of the methods. These review literature studies have proved the importance of increasing useable daylight in terms of energy efficiency and visual comfort, which defines the correctness and sensitivity of investigations in this area. This problem motivates writers to do study in this area. Various daylight and visual comfort methods were addressed, with the majority of the simulations treating the Skylight as a light roof or window on the roof. Other research focused on the various methods to the Skylight of the (Table 1). This preliminary work aims to develop a skylight massing optimization system for designers and practitioners. To receive light from above and the Skylight's influence on daylight performance, minimal cooling demand, and glare reduction.
3. Research method
The simulation and optimization approach, as well as the software, are required in the building review simulation (Fig. 1). This investigation has five components. The purpose of this research is stated in the introduction part, followed by a section that examines previous documents regarding this issue. The technique used to explore, assess, and Skylight optimize case studies is stated in the third part. The fourth part presents the results, together with an explanation of the link between skylight percentage, daylighting, and cooling and heating needs. The fifth and final component assesses the best skylight foundation in terms of glare in two seasons.
3.1. Mathematical expression of multi-objective function
In this article, database conception, examination, comparison, and optimization methods were applied to determine the connection between skylight design parameters and daylighting metrics. This research studied multiple investigations of skylights from various situations and forms to derive the attended methodologies and outcomes applied in former experiments. The examination involved skylights in various geometry and design arrangements moreover. In this paper, three objectives related to the skylight's form, including cooling and heating, UDI, need to be examined simultaneously to improve the refurbishing construction act by reducing energy waste and increasing daylighting, withdrawing too brightly and insufficiently lighted spaces approximately feasible. Therefore, it must be an optimization problem that includes multiple objective functions. This study sets multiple objective functions optimization criteria to optimize the UDI and minimize the cooling and heating demand. Get better non-dominated Pareto optimal solutions; a developed non-dominated sorting genetic algorithm-II (NSGA-II) is proposed. In numerical expressions, a multi-objective optimization problem is defined equally Eq. (3)
If any objective purpose should be increased, it is equal to reduce its adverse. The concept of X is signified by \( Y\in R^n \). A component \( \underset{\rm X}{\rm \rightarrow}\in X\ \) is named a possible decision. A vector \( \underset{\rm Z}{\rm \rightarrow}≔ \underset{\rm f}{\rm \rightarrow} \left(\underset{\rm x}{\rm \rightarrow} \in R^n\right)\) for a feasible solution \( \underset{\rm x}{\rm \rightarrow} \) Is termed an objective vector. Hence, Pareto optimal answers; that is, answers cannot be stated within either of the objectives, excluding diminishing at most limited one of the other fitness. A possible answer \( \underset{\rm X1}{\rm \rightarrow} \in X\ \) s stated to Pareto solution if : \( \underset{\rm X2}{\rm \rightarrow} \in X \)
\( {s.t. \underset{\rm X}{\rm \rightarrow} \in X,} \)To provide the architect with the best selection based on the unique challenge, an effective and comprehensive search technique must detect the kind of optimum trade-off solutions (Pareto front). A perfect point is a theoretical idea for a real-world goal in which each aim is maximized without consideration for the well-being of others. Multi-objective optimization algorithms aim to provide solutions with a well-distributed distribution that are close to the Pareto optimum front.
Wallacei [83], an analytic engine for grasshopper, is used in the optimization approach. The essence of a point set is to be appraised based on its proximity to the Pareto front; the closer the better, on the diversity in the assortment, the more evenly spread they are good. It prefers low accuracy in Monte Carlo techniques if it is also far from the set of nondominated solutions.
3.2. Utilization to a simulated case
The skylight material is not from the template and was chosen from Yuan Fanga's article [41], which has the advantage of avoiding very high temperatures and direct sunlight. The quantity of solar energy transported into the window (Solar Heat Gain Coefficient) is 0.30, while the U-Value of the material is 2.6 W/m2K. This section discusses the qualities of a material that are significant to its heat conductivity (Table 2). Besides, the skylight's dimensions and shape are determined by the factors listed in (Table 3). Since pyramid and flat skylight designs are frequently used in building architecture and have the potential to offer helpful natural illumination while lowering glare discomfort, these forms were chosen. While pyramid skylights can generate more homogeneous and diffused light, flat skylights can produce more direct and concentrated light. Flat skylights are more popular in residences, whereas pyramid skylights are widely used in business and institutional buildings. By contrasting these two types of skylights, designers may better understand how to design skylights based on their different design aims and building types. The daylighting and energy models are based on the benchmark of commercial buildings model from the US Department of Energy (DOE). OpenOffice is also used to create sets, loads, programs, and set the thermostat. The floor, external walls, interior, and the ceiling reflectance is 0.2, 0.5, 0.5, and 0.8, respectively. Variable air volume (VAV) packaged rooftop reheat assumed from ASHRAE 90.1 is considered for (HVAC) system.
Table 3
Table 3. Isfahan parameters of climate are affecting study intentions. Information was derived from the EnergyPlus database gives the weather file.
The orientation and building material are considered constraints and constant variables. The yearly direct lighting hours for the office are controlled by a single zone connected to the palace's central skylight. As shown in the case study, a 3D model was used to create a Daylight and Energy analysis (Fig. 2). The purpose of this study is to provide a theoretical understanding of how skylight design affects energy consumption and daylight levels in the area. Since the building’s length, depth and height also play a role in the optimization, this model was chosen based on the hypothesis of the authors. It is certain that the architectural features and materials of the building are in harmony with the climate of Isfahan. The skylight is located in the middle of the roof to investigate the impact of modifying the goals' factors. The form and height of the skylight are determined by two factors (v 4, v 5). The walls are finished with white plaster, the floor is covered with grey tiles, and the ceiling is white plaster 0.03 m, Extended Polystyrene 0.10 m, Hollow brick Massonary 0.15 m, Mortar 0.03 m are the four layers of construction material accessible in Isfahan's official structures. Additional aspects of the subject matter are shown in (Table 2). The total U-value and reflectance inside and outdoors for the external wall are 0.329 W/m2K and 50 percent and 35 percent, respectively. The ceiling, floor, and interior walls reflectance is 80 percent, 20 percent, and 50 percent, respectively [84]. Exteriors that are completely enclosed are termed adiabatic. The heating and cooling setpoints are 20 and 26 degrees Celsius during the weekdays. 10.1 W/m2 was chosen as the lighting power density per area. For towns in Climate Zone Number 3 and Climate Zone Subtype B, the window is composed of a double glass window with a tight air pocket established on ASHRAE 169 [13]. The Solar Heat Gain Coefficient, Thermal Transmittance, and Visible Light Transmittance of the window glass in question are 0.25, 0.65, and 0.45 W/m2K, respectively.
3.2.1. Explanation of the climate zones
Based on the Köppen climate classification system, Isfahan in Iran falls into the category of "BSk" climate. This means that the climate is dry with a semi-arid or steppe climate, characterized by hot summers and cool winters. The "B" in the code refers to a dry climate, while the "S" indicates that the dry season occurs during summer, and the "k" indicates that the mean temperature of the warmest month is above 22°C. In Isfahan the average maximum temperature of the coldest month (January) is 2°C, and the hottest month (July) is 35°C. The climate parameters are summed up in (Table 3).
3.3. Optimization objectives
Managing the energy usage for cooling and heating, daylighting, and viewing outside is a mathematical optimization issue of skylight design. The computer-aided program Rhinoceros and Grasshopper plugins are used to handle the variables in the office room simulation. Finite-dimensional models are useful in design examination in a variety of dynamic design scenarios, such as the form and proportions of skylights in this study.
The UDI in the range of 100-2000 lux is mentioned in this article, although it is inadequate to define consumers' visual comfort. The UDI describes the correct proportion of daylight that enters the office floor. As a result, the aforementioned metric that may distinguish consistent light exposure for the workplace that performs visual comfort is referred to as the absence of glare. Accordingly, overlighting causes an increase in cooling and, in certain cases, heating demand. As a result, a multi-objective optimization approach is used to achieve the requisite equivalency between lowering cooling and heating demand while enhancing UDI. This study proposes a design optimization strategy. It is feasible to produce a seasonal building execution in daylight and energy performance throughout the year simulation using an optimization method that manages difficult design forms.
In accordance with (Fig. 1), the preliminary experimental evidence is created, and then multi-objective optimization is used to determine which fact-based conclusion is the best match. The weighting approach is used in this work to discover the best-suited solution in the Pareto front. For all Pareto front replies, the variation in EUI, the fitness function drives daylight, was calculated. In this study, three goals are optimized initially, and then the fitness function is measured above the Pareto front to rank these responses and attain the fittest.
3.4. Glare analysis
Skylights may offer natural lighting while also lowering the energy wasted by buildings' electric lighting. Despite this, the skylight design usually reveals glare difficulties that make people uncomfortable [67]. The Pareto front achieves the result of measuring the amount of DGP in two consecutive seasons, both winter and summer since glare is another key metric to determine passengers' visual comfort. The sun's path is therefore seen in (Fig. 3) for December and June. The unpleasant glare is generally mitigated in a similar circumstance with a window on the building's lateral side by employing the window's shade glare protection [14]. The glare analysis of the form supplied by optimization is presented based on the occupants' placement in the simulated office (Fig. 4). It is crucial to mention that in this study the building is not surrounded by any obstacles such as trees and other buildings.
Figure 4
Fig. 4. The occupant and environment's situation for glare analysis. The analysis plane is also seen for daylight analysis.
4. Results and analysis
First, we determined the identical opening in both models in this part to comprehend the skylight's value concerning the window. The diagram shows that the window to wall ratio (WWR) is the same as the skylight to roof ratio (Fig. 5). The window to wall ratio (WWR) is tested using a different seed in the (a) model, and there are no significant variations in the results. As a result, model (a) is representative of the other forms generated. In (Fig. 5), model (b) is a sample of skylight shapes with the same aperture as the model (a). This section demonstrates that the UDI in the model (a) is less than the skylight amount, and the illumination on the floor is not uniform. Furthermore, when the building contains a lateral window, the cooling demand is greater than 90, as shown in (Fig. 6(a)). The image's cooling market (Fig. 6(b)), on the other hand, specifies less than 7 (kWh). Although from the aspect of the spiritual feeling, the human mind may prefer the lateral window, the main goal of this study is to optimize the skylight with the aim of reducing energy consumption, intensifying daylight efficiency, and visual comfort, while maintaining the trade-off between daylighting, cooling demand, and glare.
The features of the design skylight are explained in the next section. We study numerous forms using several relevant factors to discover the best skylight shape for the workplace. With the aim of reducing energy consumption, increasing daylight availability, and diminishing discomfort glare, the optimization approach modifies five elements in (Table 4). Parameters such as building’s Length, Depth, and Height as well as Skylight to Floor Ratio, and Skylight_ Roof are evaluated to meet these goals. There is a necessity for agreement in the Pareto Frontier seen in (Fig. 7). Optimal designs do not deliver optimal solutions for every objective function in a multi-objective issue with conflicting fitness. On the other hand, the optimal strategies achieve the best-compromise resolution of each target function.
Multi-objective optimization is used in this research. Using Pareto's [13] statistical technology, various grades are integrated and studied. Multiple non-dominant grades are evaluated, and ideal values for the constructed "border" in the solution diagram are identified. A single-dimensional value is displayed on one axis in (Fig. 7). Three benchmarks are assumed in a three-dimensional network, from which parametric simulation results and postprocessing using Wallacei Grasshopper plugins are created. The UDI is represented by the X-axis, while the Y-axis represents cooling energy consumption, and the Z-axis represents heating energy consumption. The finest feasible solutions in the Pareto Front are particularly informative for outlining skylights. Architects and engineers may choose the best skylight design from this collection of the finest available options for any specific purpose, guaranteeing that the desired optimal solutions are used.
The Pearson correlation coefficients are recorded in the collection of produced solutions for each set of response variables, as seen in (Table 5). These strongest correlations for all response variables with a negative quantity, especially Y1 with Y2 and Y2 with Y3, indicate that these response variables are conflicted. When the UDI raises the amount of the cooling reduction, it signifies that the cooling demand is lower in the summer than in the winter, despite the fact that the heating demand is higher in the winter. The designer focuses more on cooling in a hot environment to conserve energy since the inhabitants utilize cooling systems to remain in their comfort zone most of the year. There is a strong negative association between Y1, which represents usable daylight illuminance, and Y2, which means cooling demand.
In objective space, the nine Pareto solutions (boxes) are recognized as the simultaneous decrease and maximization of all the response variables shown in (Fig. 7). We specify the representation of the received answers for Y1, Y2, and Y3 such that all response variables have substantial correlations.
The Pareto front solution is greater, as shown in (Fig. 7); so, the chosen solutions in (Table 6) are the final generation with optimum values for the design variables, i.e., in the range of 0 to 4 individuals. Although the Pareto front suggests nine solutions, only four solutions satisfy the goal, for the reason that we look for the trade-off between the four selected parameters. The acceptable solutions indicators, Y2, are not included here since their value equals 0.40 for each skylight response gathered. We evaluate the Skylight, which has a Skylight to Floor Ratio of 0.70 and a Skylight Roof Ratio of 0.30, making the pyramid shape more appropriate for an office with a length of 10 meters, a depth of 8 meters, and a height of 3.6 meters. The variables listed in (Table 6) produce various shapes such as box and flat skylights and pyramids with varying ratios. Despite this, all of the best solutions have pyramid shapes.
As shown in (Fig. 8), the objectives in solutions 1 and 2 are more valuable than answers 3 and 4. It means that the cooling amount is more than the amount of helpful daylight illuminance is less than solutions 3 and 4.
Using a skylight to floor ratio of 0.70, optimally compromised values for both the UDI and Cooling energy were attained for both square and rectangular shape roofs. Solution 1 and 2 have a high skylight to roof ratio, which allows for the greatest amount of daylight to enter the room, resulting in high UDI values and a reduced cooling demand while maintaining the same level of heating. Figure 9 demonstrates that the solutions provided only modest amounts for energy use. According to the climate of Isfahan, cooling energy is consumed from mid-May to mid-October. Additionally, the heating energy consumption season spans from November through March. The preliminary summary information for the Pareto front solutions is presented in (Table 6). As a consequence of the previous findings for Y1 indicating UDI, the great majority of solutions have a value between 0.951 and 0.591. The value of y2, which stands for cooling, ranges between 40.4 and 55.5.
Furthermore, the Pareto front redline in (Fig. 10) shows that the generation's final individual. These lines suggest that a high UDI round of 0.95 and cooling around 45 may be achieved. When they reduce cooling demand, they increase heating demand, and the two have inverse effects; the heating average in this climatic zone is not high. The goal of this study, on the other hand, is to minimize cooling when the UDI is high.
Only taking into consideration UDI measures in the last segment is not sufficient for virtual comfort. Consequently, after determining the most appropriate skylight type, we investigate glare in both winter and summer at different times of the day. If the quantity of DGP is less than 0.30, it is unnoticeable, and if the amount is more than 0.45, it is unbearable [85]. As can be shown in Figure, the quantity of DGP is 0.200 with all solutions, and the glare comfort ranges from invisible glare to imperceptible glare. Solution1 with a skylight to floor ratio of 0.70 provided for little cooling demand while maintaining high UDI (0.951913) and DGP (0.183964) in the summer and (0.200679) in the winter, indicating high-quality daylight entering the area that allows for occupants' visual comfort in all seasons (Table 7).
Figure 11
Fig. 11. DGP in the optimal solutions in the Pareto front, View-direction dependent glare evaluations.
Both sceneries were produced at midday on December 21st and June 21st, respectively, in (Fig. 11) under clear CIE sky conditions on both days. All of the photographs have false-color evaluations of glare measures presented over the bottom of each image. Each example includes a timestamp corresponding to the month, day, and hour setup.
All of the options provide a high level of visual comfort for occupants with the least amount of glare potential while also allowing for a high level of daylight into the room without warming the space or increasing the amount of cooling required, as demonstrated in the diagram (Fig. 12).
5. Conclusion
There is a discussion of the analytical and methodological gap in arranging skylights for the design of office buildings in this work. The immediate consequences of the impact of skylight design on the quality and execution of a building's quality and performance include energy efficiency, daylight savings, and aesthetic comfort. According to the studied literature, there was a limit in terms of introducing a dependable link between the building's features and skylight geometry into the design. The information pertaining to the skylight design has been viewed as a single surface in various configurations. This article developed a technique for determining the ideal skylight shape in a hot climatic zone in order to decrease energy consumption while increasing beneficial daylight.
First and foremost, this study seeks to comprehend the importance of the skylight concerning the window on the wall during hot weather. So, the conclusion that is drawn from the initial analysis is that the skylight delivers sufficient daylight illumination for the purposes of the project. When the building is equipped with windows, the quantity of cooling required is lower.
The goal of this article is to determine the ideal skylight shape in order to reduce energy consumption while increasing useable daylight in the second section. Grasshopper plugins (Ladybug and Honeybee) are used to compute energy consumption as well as usable daytime illuminance using the 3D model, Rhinoceros, and two Grasshopper plugins (Ladybug and Honeybee). The NSGA-II optimization method, which generates a collection of optimum solutions, is useful for architectural firms.
The optimum solutions demonstrated the effectiveness of the optimization framework in reaching the optimal skylight shape for each of the objectives under consideration. Among all the proposed solutions in (Fig. 7), there are four that satisfy the goal in terms of reducing energy consumption and increasing daylight efficiency. As can be seen from (Fig. 12), solution 1 has a high UDI value. Also, compared to other suggested cases, the amount of cooling has been kept at its lowest level. On the other hand, it is perceived that despite the trivial difference compared to other cases, the heating value is at the highest level. In solution 2, UDI has an upward trend and the cooling value is intensified with a negligible difference compared to the previous model. Although solution 3 has an acceptable value in the range of 100-2000, it has the lowest rate among the competitors. It is clear that in the fourth solution, the value of UDI and cooling are both higher than the previous ones, and that is probably due to the intensification of the roof height. On the basis of the optimal forms proposed, the pyramidal form with a skylight to floor ratio of 0.70, which has the floor that has the largest area on the roof of the building and the skylight's top, which is approximately half the floor area (0.30), is suitable for a room with both a cube and a rectangular cube shape on the ceiling of the building. These ideal skylights provide the most appropriate light while using the least amount of electricity. This study's findings indicate that generating an undistorted digital image for more than 90 percent of the reference room locations while limiting energy consumption is feasible. At the same time, the DGP measurements for visual comfort are being investigated in this study. Each of the Pareto front's optimum solutions has a DGP in the range of unnoticeable glare between 0.151 and 0.260 for the summer and winter solstices, respectively.
A multi-objective optimization technique generates a number of options rather than searching for a single optimal solution because the study aims to optimize the skylight design based on various performance factors. The authors fully acknowledge the limitations of this study as it can be difficult to identify a single ideal solution that meets all requirements. Despite all the limitations, the present study's technique can help designers create well-informed skylight designs that produce high-quality indoor environments while consuming less energy. By demonstrating the practicality of the recommended NSGA-II optimization technique and providing a benchmark by which to assess the effectiveness of skylight designs, our research may aid future investigations. Further research can enhance the optimization model and expand its applicability to different building types and environmental contexts.
Contributions
All the authors contributed equally.
Declaration of competing interest
The authors declare no conflict of interest.
References
- A. D. Galasiu, and J. A. Veitch, Occupant preferences and satisfaction with the luminous environment and control systems in daylit offices: a literature review, Energy and buildings 38 (2006) 728-742. https://doi.org/10.1016/j.enbuild.2006.03.001
- M. B. Aries, M. P. Aarts, and J. van Hoof, Daylight and health: A review of the evidence and consequences for the built environment, Lighting Research & Technology 47 (2015) 6-27. https://doi.org/10.1177/1477153513509258
- L. Sharma, K. Kishan Lal, and D. Rakshit, Evaluation of impact of passive design measures with energy saving potential through estimation of shading control for visual comfort, Journal of Building Physics 42 (2018) 220-238. https://doi.org/10.1177/1744259117742989
- N. T. Al-Ashwal and I. M. Budaiwi, Energy savings due to daylight and artificial lighting integration in office buildings in hot climate, International Journal of Energy and Environment 2 (2011) 999-1012.
- A. Goharian and M. Mahdavinejad, A novel approach to multi-apertures and multi-aspects ratio light pipe, Journal of Daylighting 7 (2020) 186-200. https://doi.org/10.15627/jd.2020.17
- R. M. Reffat and R. M. Ahmad, Determination of optimal energy-efficient integrated daylighting systems into building windows, Solar Energy 209 (2020) 258-277. https://doi.org/10.1016/j.solener.2020.08.086
- M. Mohsenin and J. Hu, Assessing daylight performance in atrium buildings by using Climate Based Daylight Modeling, Solar Energy 119 (2015) 553-560. https://doi.org/10.1016/j.solener.2015.05.011
- M. B. Aries, J. A. Veitch, and G. R. Newsham, Windows, view, and office characteristics predict physical and psychological discomfort, Journal of environmental psychology 30 (2010) 533-541. https://doi.org/10.1016/j.jenvp.2009.12.004
- A. Borisuit, F. Linhart, J-L. Scartezzini, and M. Münch, Effects of realistic office daylighting and electric lighting conditions on visual comfort, alertness and mood, Lighting Research & Technology 47 (2015) 192-209. https://doi.org/10.1177/1477153514531518
- E. L. Krüger, C. Tamura, and T. W. Trento, Identifying relationships between daylight variables and human preferences in a climate chamber, Science of the Total Environment 642 (2018) 1292-1302. https://doi.org/10.1016/j.scitotenv.2018.06.164
- B. Fakhr and M. Mahdavinejad, The Effect of Lighting the Buildings on the Perception of People from the Color Temperature of Light, J Archit Eng Tech 7 (2018) 1000211. https://doi.org/10.4172/2168-9717.100021
- S. Proietti, U. Desideri, P. Sdringola, and F. Zepparelli, Carbon footprint of a reflective foil and comparison with other solutions for thermal insulation in building envelope, Applied energy 112 (2013) 843-855. https://doi.org/10.1016/j.apenergy.2013.01.086
- M. Khoroshiltseva, D. Slanzi, and I. Poli, A Pareto-based multi-objective optimization algorithm to design energy-efficient shading devices, Applied energy 184 (2016) 1400-1410. https://doi.org/10.1016/j.apenergy.2016.05.015
- K. Lai, W. Wang, and H. Giles, Solar shading performance of window with constant and dynamic shading function in different climate zones, Solar Energy 147 (2017) 113-125. https://doi.org/10.1016/j.solener.2016.10.015
- F. Kheiri, A review on optimization methods applied in energy-efficient building geometry and envelope design, Renewable and Sustainable Energy Reviews 92 (2018) 897-920. https://doi.org/10.1016/j.rser.2018.04.080
- S. M. Al-Masrani, K. M. Al-Obaidi, N. A. Zalin, and M. A. Isma, Design optimisation of solar shading systems for tropical office buildings: Challenges and future trends, Solar Energy 170 (2018) 849-872. https://doi.org/10.1016/j.solener.2018.04.047
- M. Rabani, H. B. Madessa, and N. Nord, Achieving zero-energy building performance with thermal and visual comfort enhancement through optimization of fenestration, envelope, shading device, and energy supply system, Sustainable Energy Technologies and Assessments 44 (2021) 101020. https://doi.org/10.1016/j.seta.2021.101020
- S. Carlucci, G. Cattarin, F. Causone, and L. Pagliano, Multi-objective optimization of a nearly zero-energy building based on thermal and visual discomfort minimization using a non-dominated sorting genetic algorithm (NSGA-II), Energy and Buildings 104 (2015) 378-394. https://doi.org/10.1016/j.enbuild.2015.06.064
- E. Dolnikova, D. Katunsky, and S. Darula, Assessment of overcast sky daylight conditions in the premises of engineering operations considering two types of skylights, Building and Environment 180 (2020) 106976. https://doi.org/10.1016/j.buildenv.2020.106976
- S. Lou et al., A study of the skylight coverage ratio for air-conditioned atriums in the hot and humid regions, International Journal of Low-Carbon Technologies 16 (2021) 946-955. https://doi.org/10.1093/ijlct/ctab023
- R. Sokkar and H. Z. Alibaba, Thermal comfort improvement for atrium building with double-skin skylight in the mediterranean climate, Sustainability 12 (2020) 2253. https://doi.org/10.3390/su12062253
- R. Lapisa et al., Effect of skylight-roof ratio on warehouse building energy balance and thermal-visual comfort in hot-humid climate area, Asian Journal of Civil Engineering 21 (2020) 915-923. https://doi.org/10.1007/s42107-020-00249-9
- F. Zhengyu and Z. Yihua, Numerical Investigation of key design parameters impact on energy consumption of commercial complex distributed atrium in cold area of China, in: IOP Conference Series: Earth and Environmental Science, 2020, 012024. https://doi.org/10.1088/1755-1315/531/1/012024
- D. P. Laksmiyanti and R. P. Salisnanda, Optimization of skylight composition for cooling and lighting energy efficiency (Case Study: G-building ITATS), International Journal of Advanced Engineering Research and Science 5 (2018) 268255. https://doi.org/10.22161/ijaers.5.11.37
- T. Du and J. Chen, Skylight Optimization Design Based on the Interior Ventilation in the Office Building in Cold Region, in: Mediterranean Green Buildings & Renewable Energy, 2017, pp. 691-699. https://doi.org/10.1007/978-3-319-30746-6_53
- Z. Shirzadnia, A. Goharian, and M. Mahdavinejad, Designerly approach to skylight configuration based on daylight performance; Toward a novel optimization process, Energy and Buildings 286 (2023) 112970. https://doi.org/10.1016/j.enbuild.2023.112970
- Y. Xue and W. Liu, A Study on Parametric Design Method for Optimization of Daylight in Commercial Building's Atrium in Cold Regions, Sustainability 14 (2022) 7667. https://doi.org/10.3390/su14137667
- F. Piraei, B. Matusiak, and V. R. Lo Verso, Evaluation and Optimization of Daylighting in Heritage Buildings: A Case-Study at High Latitudes, Buildings 12 (2022) 2045. https://doi.org/10.3390/buildings12122045
- S. Nazari, B. Sajadi, and I. Sheikhansari, Optimisation of commercial buildings envelope to reduce energy consumption and improve indoor environmental quality (IEQ) using NSGA-II algorithm, International Journal of Ambient Energy (2023) 1-11. https://doi.org/10.1080/01430750.2022.2157482
- M. Baghoolizadeh et al., Multi-objective optimization of Venetian blinds in office buildings to reduce electricity consumption and improve visual and thermal comfort by NSGA-II, Energy and Buildings 278 (2023) 112639. https://doi.org/10.1016/j.enbuild.2022.112639
- N. Rafati, M. Hazbei, and U. Eicker, Louver configuration comparison in three Canadian cities utilizing NSGA-II, Building and Environment 229 (2023) 109939. https://doi.org/10.1016/j.buildenv.2022.109939
- W. C. Chishimba, Strategies for Motivating Sales Employees' Performance within Small Business in the United States, Walden University ProQuest Dissertations Publishing, 2018.
- M. Amer, J. L. Moro, and S. Attia, Parametric analysis for daylight autonomy and energy consumption in hot climates, in: 13th International Conference of the International Building Performance Simulation Association, 2013, pp. 2232- 2240, France.
- X. Shi, T. Abel, and L. Wang, Influence of two motion types on solar transmittance and daylight performance of dynamic façades, Solar Energy 201 (2020) 561-580. https://doi.org/10.1016/j.solener.2020.03.017
- L. Santos, A. Leitão, and L. Caldas, A comparison of two light-redirecting fenestration systems using a modified modeling technique for Radiance 3-phase method simulations, Solar energy 161 (2018) 47-63. https://doi.org/10.1016/j.solener.2017.12.020
- A. Toutou, M. Fikry, and W. Mohamed, The parametric based optimization framework daylighting and energy performance in residential buildings in hot arid zone, Alexandria Engineering Journal 57 (2018) 3595-3608. https://doi.org/10.1016/j.aej.2018.04.006
- T. Ariosto, A. M. Memari, and R. L. Solnosky, Development of designer aids for energy efficient residential window retrofit solutions, Sustainable Energy Technologies and Assessments 33 (2019) 1-13. https://doi.org/10.1016/j.seta.2019.02.007
- G. Sancer et al., Modality-specific circuits for skylight orientation in the fly visual system, Current Biology 29 (2019) 2812-2825. https://doi.org/10.1016/j.cub.2019.07.020
- A. Chel, G. Tiwari, and A. Chandra, A model for estimation of daylight factor for skylight: an experimental validation using pyramid shape skylight over vault roof mud-house in New Delhi (India), Applied Energy 86 (2009) 2507-2519. https://doi.org/10.1016/j.apenergy.2009.03.004
- E. L. Skov et al., Roof panel assembly with skylight, U.S. Patent 7,721,493, 2010.
- Y. Fang and S. Cho, Sensitivity Analysis of Skylight and Clerestory Design on Energy and Daylight Performance of a Retail Building (C023), in: 2018 Building Performance Analysis Conference and SimBuild, 2018.
- A. Aldawoud, The influence of the atrium geometry on the building energy performance, Energy and Buildings 57 (2013) 1-5. https://doi.org/10.1016/j.enbuild.2012.10.038
- A. Chel, Performance of skylight illuminance inside a dome shaped adobe house under composite climate at New Delhi (India): A typical zero energy passive house, Alexandria Engineering Journal 53 (2014) 385-397. https://doi.org/10.1016/j.aej.2014.01.006
- P. Pilechiha et al., Multi-objective optimisation framework for designing office windows: quality of view, daylight and energy efficiency, Applied Energy 261 (2020) 114356. https://doi.org/10.1016/j.apenergy.2019.114356
- A. Meresi, Evaluating daylight performance of light shelves combined with external blinds in south-facing classrooms in Athens, Greece, Energy and Buildings 116 (2016) 190-205. https://doi.org/10.1016/j.enbuild.2016.01.009
- M. B. Piderit Moreno and C. Yañez Labarca, Methodology for assessing daylighting design strategies in classroom with a climate-based method, Sustainability 7 (2015) 880-897. https://doi.org/10.3390/su7010880
- R. Mistrick, C. Casey, L. Chen, and S. Subramaniam, Computer modeling of daylight-integrated photocontrol of electric lighting systems, Buildings 5 (2015) 449-466. https://doi.org/10.3390/buildings5020449
- Z. Wang and J. Zhao, Optimization of passive envelop energy efficient measures for office buildings in different climate regions of China based on modified sensitivity analysis, Sustainability 10 (2018) 907. https://doi.org/10.3390/su10040907
- Y. Zhai, Y. Wang, Y. Huang, and X. Meng, A multi-objective optimization methodology for window design considering energy consumption, thermal environment and visual performance, Renewable Energy 134 (2019) 1190-1199. https://doi.org/10.1016/j.renene.2018.09.024
- Y. K. Yi, A. Tariq, J. Park, and D. Barakat, Multi-objective optimization (MOO) of a skylight roof system for structure integrity, daylight, and material cost, Journal of Building Engineering 34 (2021) 102056. https://doi.org/10.1016/j.jobe.2020.102056
- W. Hee et al., The role of window glazing on daylighting and energy saving in buildings, Renewable and Sustainable Energy Reviews 42 (2015) 323-343. https://doi.org/10.1016/j.rser.2014.09.020
- P. Xue et al., Optimization of window-to-wall ratio with sunshades in China low latitude region considering daylighting and energy saving requirements, Applied Energy 233 (2019) 62-70. https://doi.org/10.1016/j.apenergy.2018.10.027
- S. M. Hosseini et al., A morphological approach for kinetic façade design process to improve visual and thermal comfort, Building and Environment 153 (2019) 186-204. https://doi.org/10.1016/j.buildenv.2019.02.040
- T. Srisamranrungruang and K. Hiyama, Balancing of natural ventilation, daylight, thermal effect for a building with double-skin perforated facade (DSPF), Energy and Buildings 210 (2020) 109765. https://doi.org/10.1016/j.enbuild.2020.109765
- T. Mavridou and L. T. Doulos, Evaluation of different roof types concerning daylight in industrial buildings during the initial design phase: Methodology and case study, Buildings 9 (2019) 170. https://doi.org/10.3390/buildings9070170
- M. Marzouk, A. Eissa, and M. ElSharkawy, Influence of light redirecting control element on daylight performance: a case of Egyptian heritage palace skylight, Journal of Building Engineering 31 (2020) 101309. https://doi.org/10.1016/j.jobe.2020.101309
- E. Cochran, et al., Integrated Dynamic Skylight Solutions to Reduce Energy Consumption and Improve Indoor Lighting Quality in US Buildings, ACEEE Summer Study on Energy Efficiency in Buildings, 2014, 39-50.
- C. E. Ochoa et al., Considerations on design optimization criteria for windows providing low energy consumption and high visual comfort, Applied energy 95 (2012) 238-245. https://doi.org/10.1016/j.apenergy.2012.02.042
- N. S. Shafavi, M. Tahsildoost, and Z. S. Zomorodian, Investigation of illuminance-based metrics in predicting occupants' visual comfort (case study: Architecture design studios), Solar Energy 197 (2020) 111-125. https://doi.org/10.1016/j.solener.2019.12.051
- J. A. Jakubiec and C. F. Reinhart, A concept for predicting occupants' long-term visual comfort within daylit spaces, Leukos 12 (2016) 185-202. https://doi.org/10.1080/15502724.2015.1090880
- P. Bakmohammadi and E. Noorzai, Optimization of the design of the primary school classrooms in terms of energy and daylight performance considering occupants' thermal and visual comfort, Energy Reports 6 (2020) 1590-1607. https://doi.org/10.1016/j.egyr.2020.06.008
- J. H. Lee, J. W. Moon, and S. Kim, Analysis of occupants' visual perception to refine indoor lighting environment for office tasks, Energies 7 (2014) 4116-4139. https://doi.org/10.3390/en7074116
- K. H. Cheong et al., A simulation-aided approach in improving thermal-visual comfort and power efficiency in buildings, Journal of Building Engineering 27 (2020) 100936. https://doi.org/10.1016/j.jobe.2019.100936
- C. Pierson, J. Wienold, and M. Bodart, Discomfort glare perception in daylighting: influencing factors, Energy Procedia 122 (2017) 331-336. https://doi.org/10.1016/j.egypro.2017.07.332
- L. Karlsen, P. Heiselberg, I. Bryn, and H. Johra, Verification of simple illuminance based measures for indication of discomfort glare from windows, Building and environment 92 (2015) 615-626. https://doi.org/10.1016/j.buildenv.2015.05.040
- P. Stone and S. Harker, Individual and group differences in discomfort glare responses, Lighting Research & Technology 5 (1973) 41-49. https://doi.org/10.1177/096032717300500106
- Z. Hamedani et al., Lighting for work: A study of the relationships among discomfort glare, physiological responses and visual performance, Building and Environment 167 (2020) 106478. https://doi.org/10.1016/j.buildenv.2019.106478
- W. K. Osterhaus, Discomfort glare assessment and prevention for daylight applications in office environments, Solar Energy 79 (2005) 140-158. https://doi.org/10.1016/j.solener.2004.11.011
- J. Y. Suk, M. Schiler, and K. Kensek, Investigation of existing discomfort glare indices using human subject study data, Building and Environment 113 (2017) 121-130. https://doi.org/10.1016/j.buildenv.2016.09.018
- J. A. Y. Garretón, E. M. Colombo, and A. E. Pattini, A global evaluation of discomfort glare metrics in real office spaces with presence of direct sunlight, Energy and Buildings 166 (2018) 145-153. https://doi.org/10.1016/j.enbuild.2018.01.024
- J. Wienold and J. Christoffersen, Evaluation methods and development of a new glare prediction model for daylight environments with the use of CCD cameras, Energy and buildings 38 (2006) 743-757. https://doi.org/10.1016/j.enbuild.2006.03.017
- C. F. Reinhart and O. Walkenhorst, Validation of dynamic RADIANCE-based daylight simulations for a test office with external blinds, Energy and buildings 33 (2001) 683-697. https://doi.org/10.1016/S0378-7788(01)00058-5
- K. Van Den Wymelenberg, M. Inanici, and P. Johnson, The effect of luminance distribution patterns on occupant preference in a daylit office environment, Leukos 7 (2010) 103-122. https://doi.org/10.1582/LEUKOS.2010.07.02003
- J. Lee, M. Boubekri, and F. Liang, Impact of building design parameters on daylighting metrics using an analysis, prediction, and optimization approach based on statistical learning technique, Sustainability 11 (2019) 1474. https://doi.org/10.3390/su11051474
- M. C. Dubois, Shading devices and daylight quality: an evaluation based on simple performance indicators, Lighting Research & Technology 35 (2003) 61-74. https://doi.org/10.1191/1477153503li062oa
- I. LM, Approved method: IES spatial Daylight autonomy (sDA) and annual sunlight exposure (ASE), Illuminating Engineering Society, USA, 2013.
- M. Marzouk, M. ElSharkawy, and A. Eissa, Optimizing thermal and visual efficiency using parametric configuration of skylights in heritage buildings, Journal of Building Engineering 31 (2020) 101385. https://doi.org/10.1016/j.jobe.2020.101385
- Y. Yılmaz and B. Ç. Yılmaz, A weighted multi-objective optimisation approach to improve based facade aperture sizes in terms of energy, thermal comfort and daylight usage, Journal of Building Physics 44 (2021) 435-460. https://doi.org/10.1177/1744259120930047
- L. Ghobad, W. Place, and J. Hu, He Impact of Systems Integration on the Daylighting Performance of Skylights in Offices, Proceedings of SimBuild 5 (2012) 577-584.
- K. M. Al-Obaidi and A. M. A. Rahman, Toplighting systems for improving indoor environment: a review, Renewable Energy and Sustainable Technologies for Building and Environmental Applications: Options for a Greener Future, Springer, Cham, 2016. https://doi.org/10.1007/978-3-319-31840-0_7
- J. Li, X. Chen, Q. Ban, and J. Yao, Skylight Sizing based on balancing Daylighting Performance and Visual Comfort in Atrium Buildings, in: IOP Conference Series: Materials Science and Engineering (556), 2019, p. 012051. https://doi.org/10.1088/1757-899X/556/1/012051
- W. El-Abd, B. Kamel, M. Afify, and M. Dorra, Assessment of skylight design configurations on daylighting performance in shopping malls: A case study, Solar Energy 170 (2018) 358-368. https://doi.org/10.1016/j.solener.2018.05.052
- M. Makki, M. Showkatbakhsh, and Y. Song, Wallacei: An Evolutionary and Analytic Engine for Grasshopper 3D, London, UK: Wallacei, 2018.
- S. Motamedi and P. Liedl, Integrative algorithm to optimize skylights considering fully impacts of daylight on energy, Energy and Buildings 138 (2017) 655-665. https://doi.org/10.1016/j.enbuild.2016.12.045
- J. Wienold, J. Christoffersen, Towards a new daylight glare rating, in: Proceedings of the 10th European Lighting Conference, Lux Europa, Lux EuropaBerlin (DE), 2005, pp. 157-161.
Copyright © 2023 The Author(s). Published by solarlits.com.
 HOME
HOME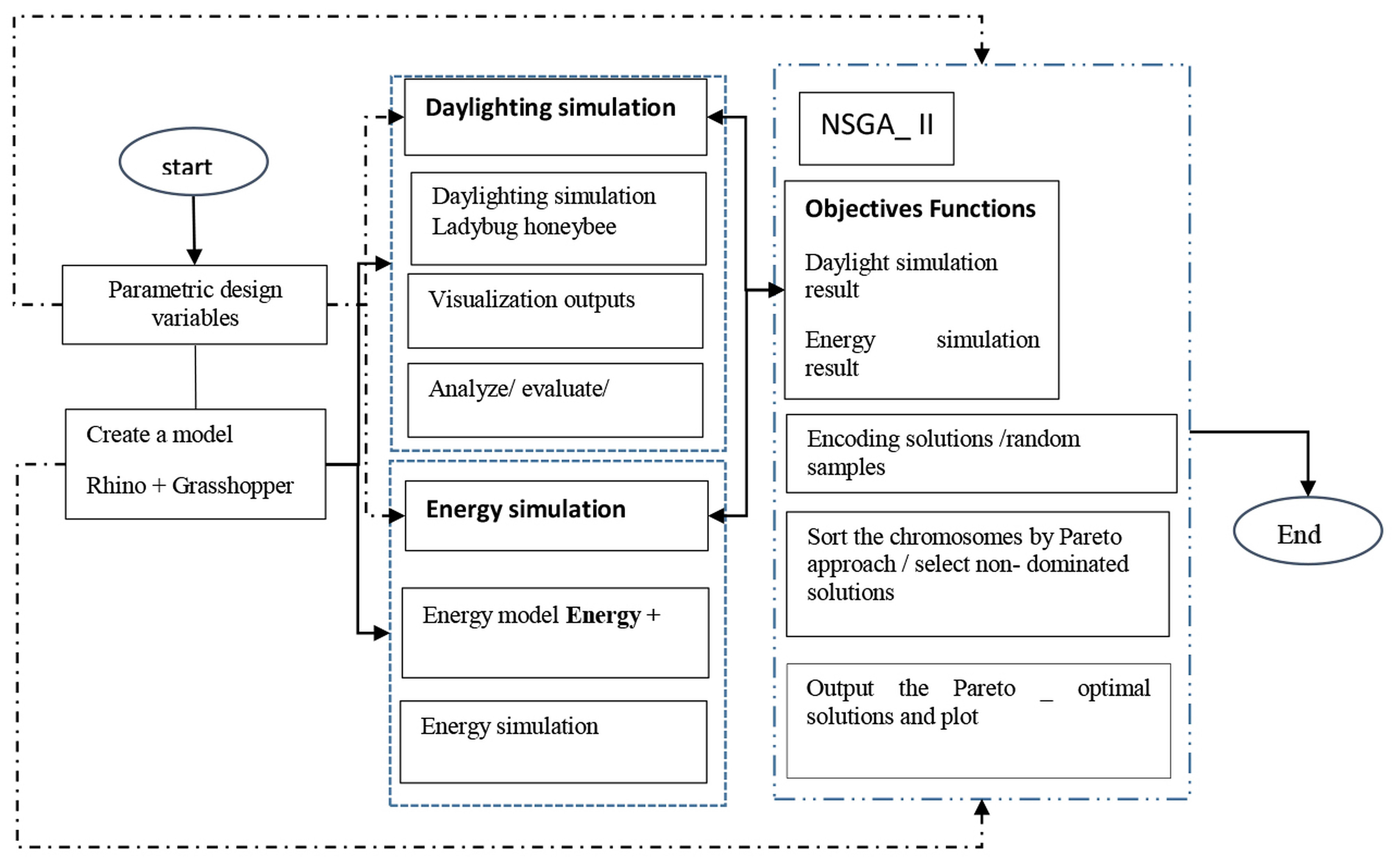 Figure 1
Figure 1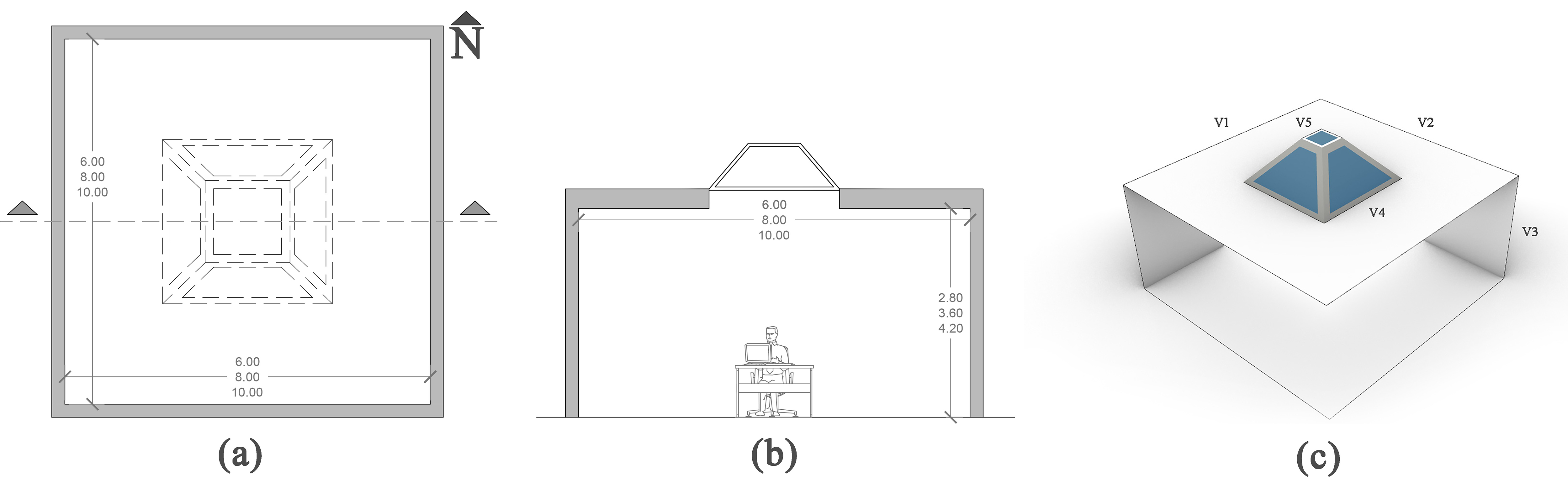 Figure 2
Figure 2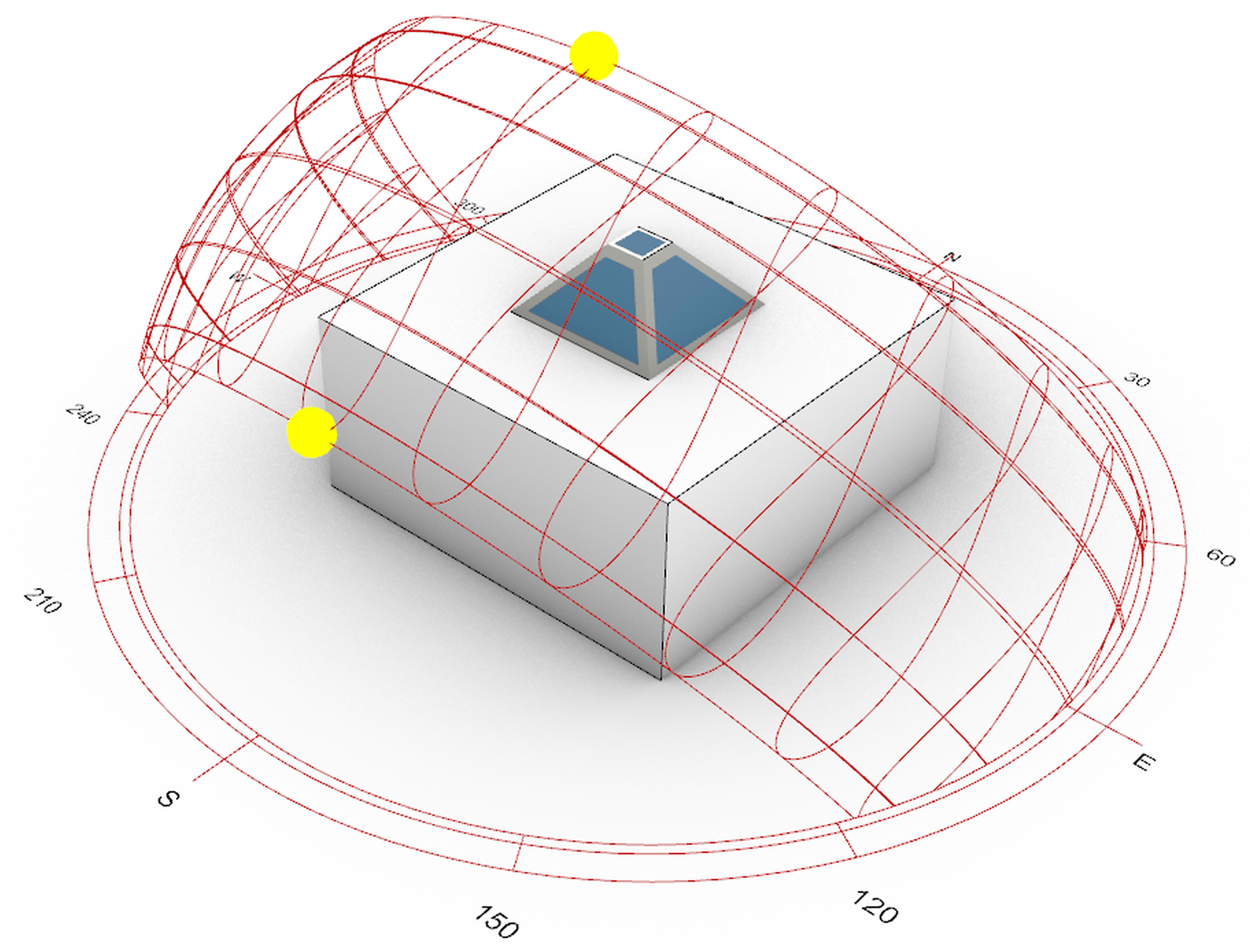 Figure 3
Figure 3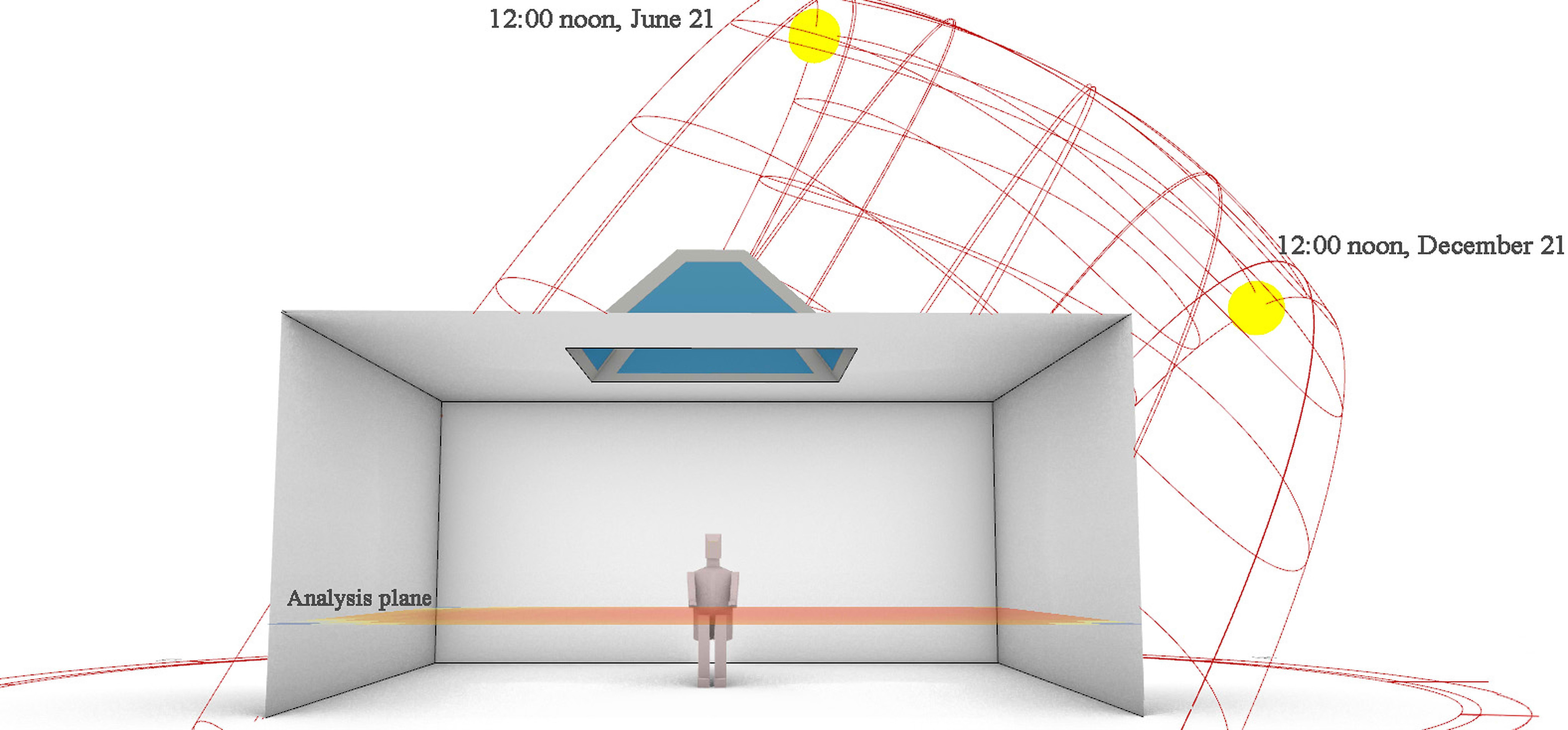 Figure 4
Figure 4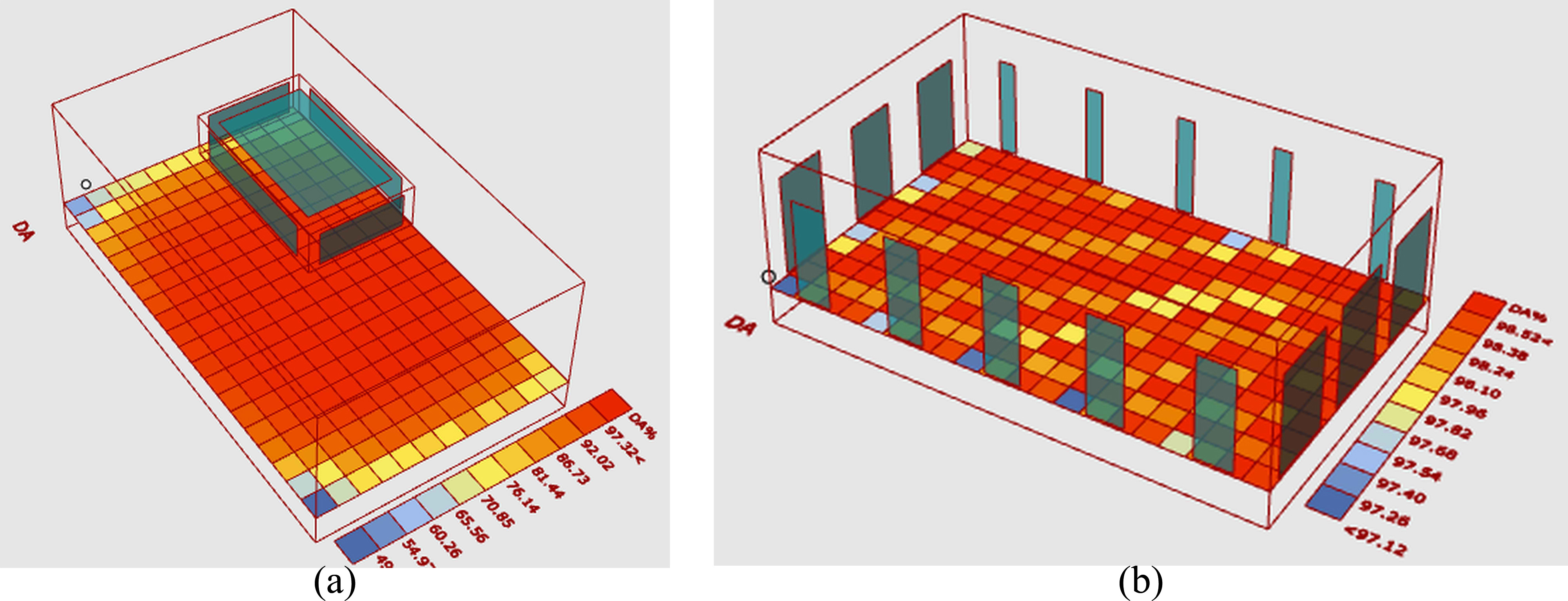 Figure 5
Figure 5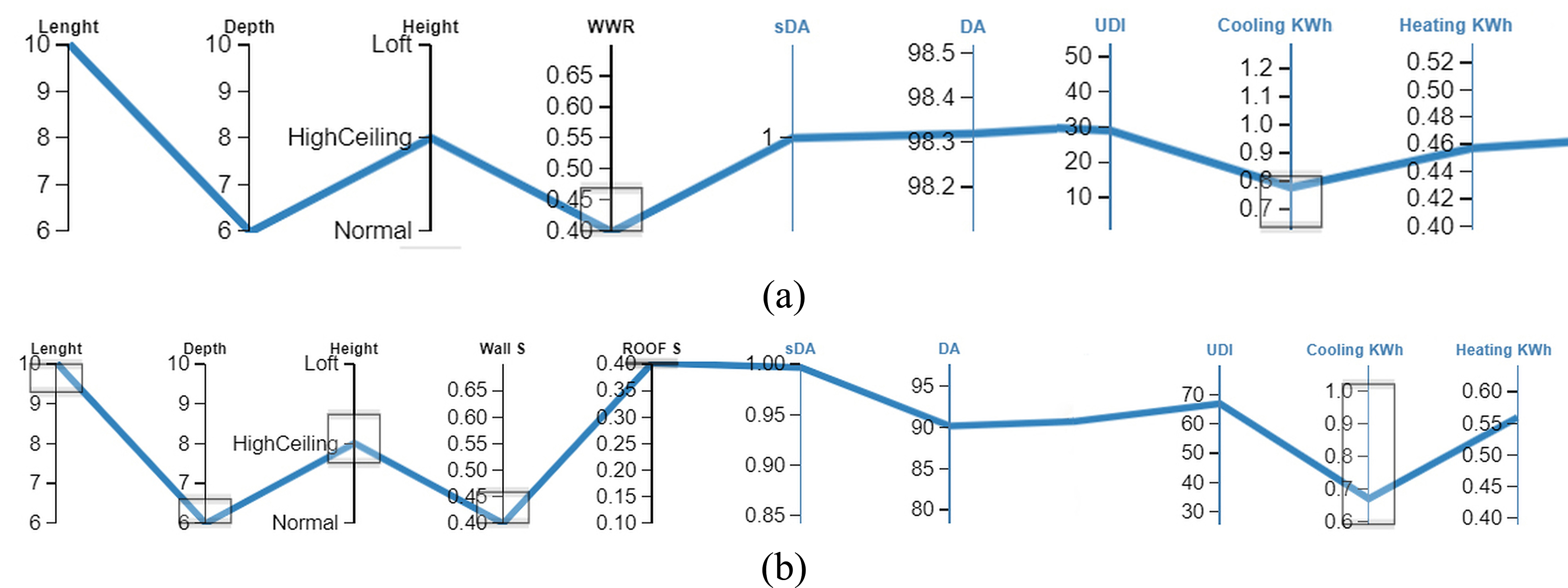 Figure 6
Figure 6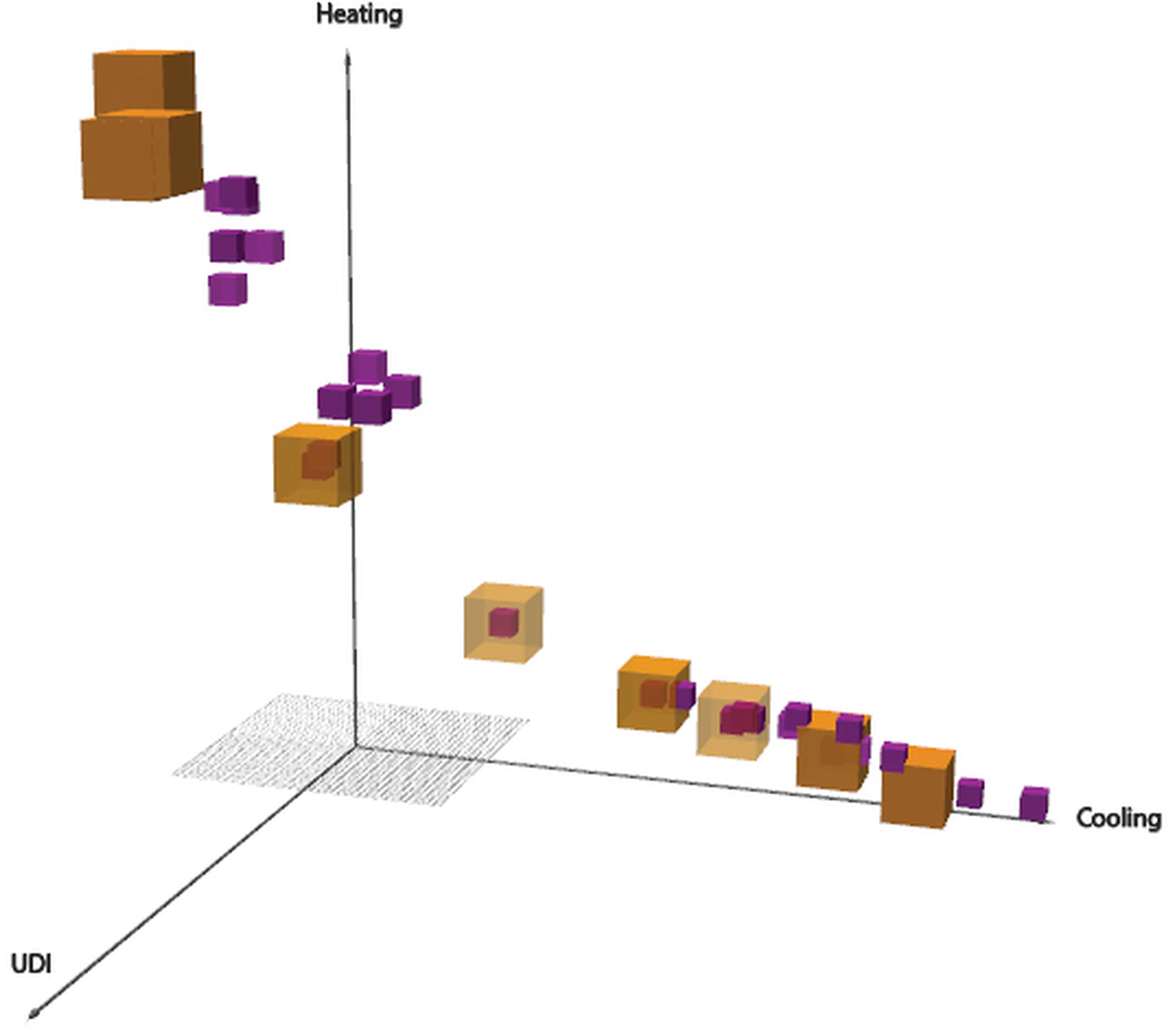 Figure 7
Figure 7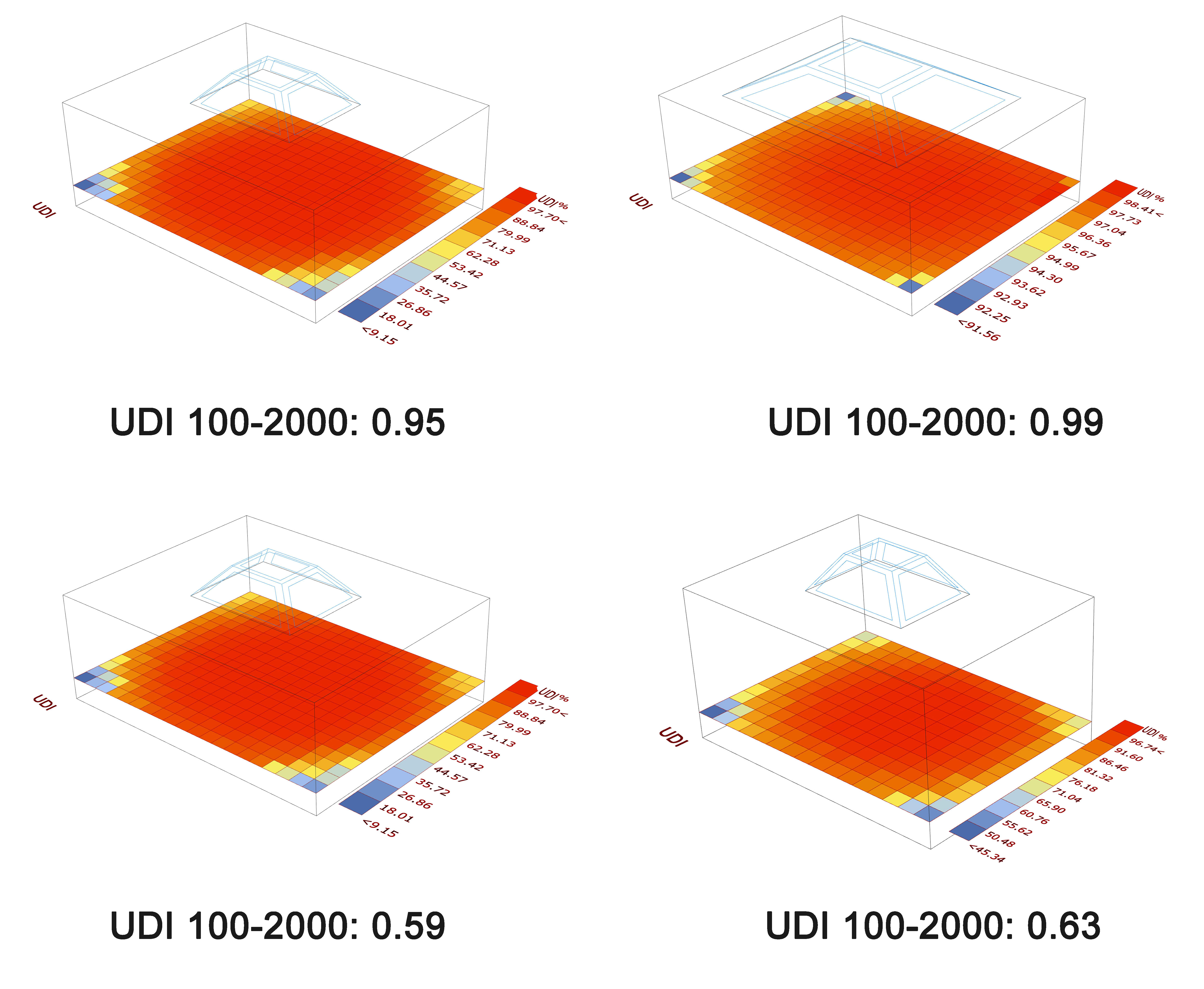 Figure 8
Figure 8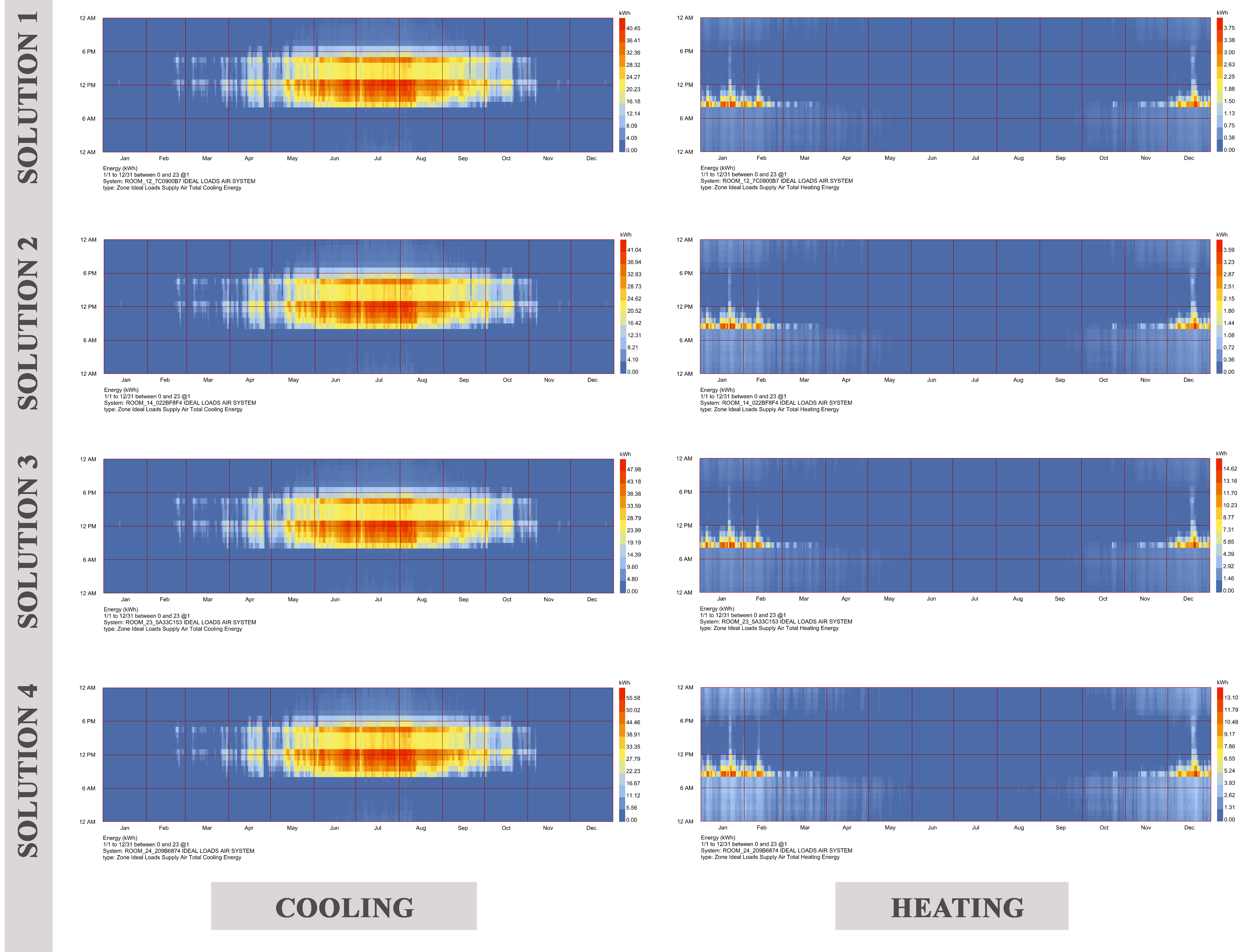 Figure 9
Figure 9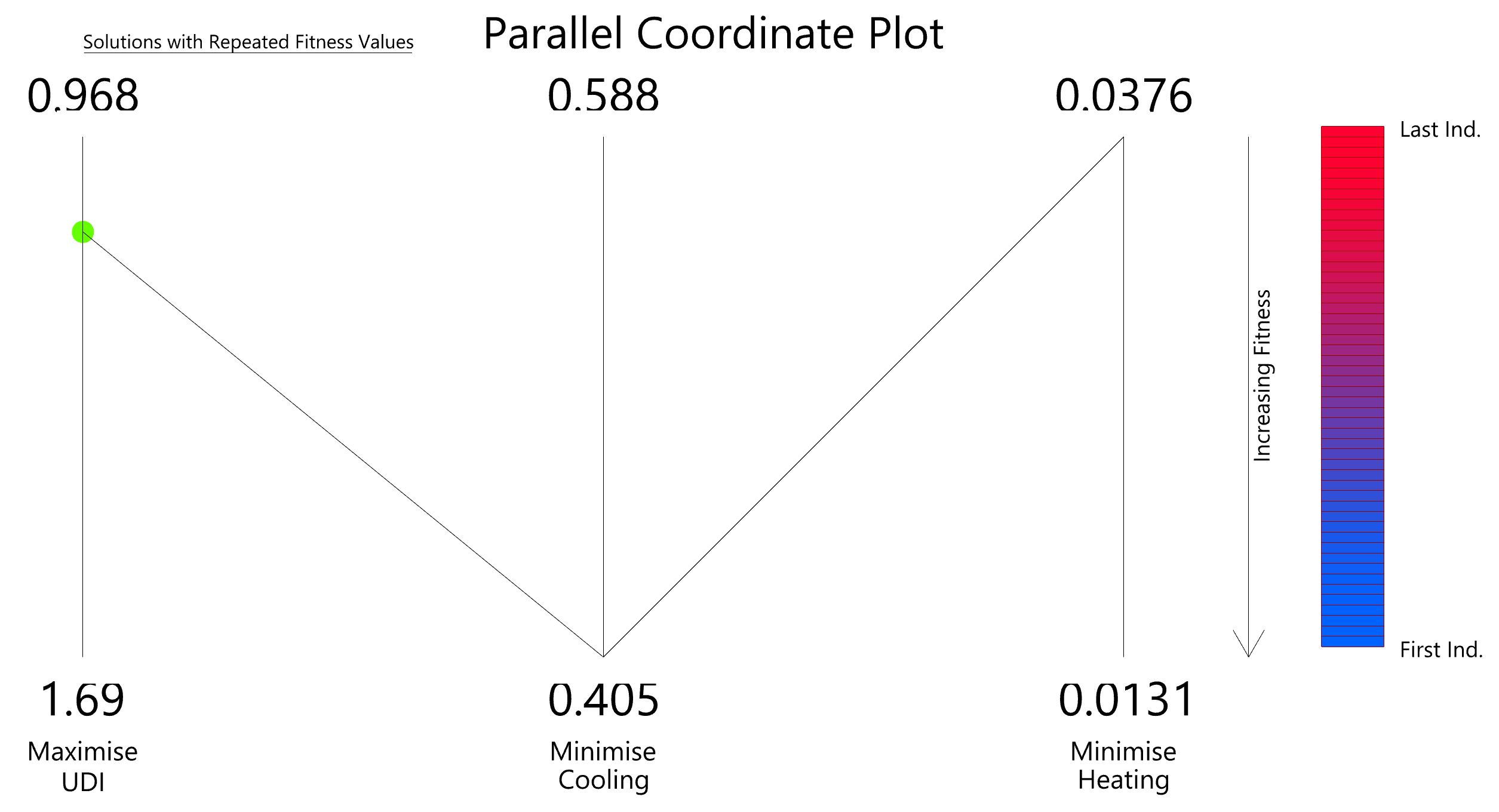 Figure 10
Figure 10 Figure 11
Figure 11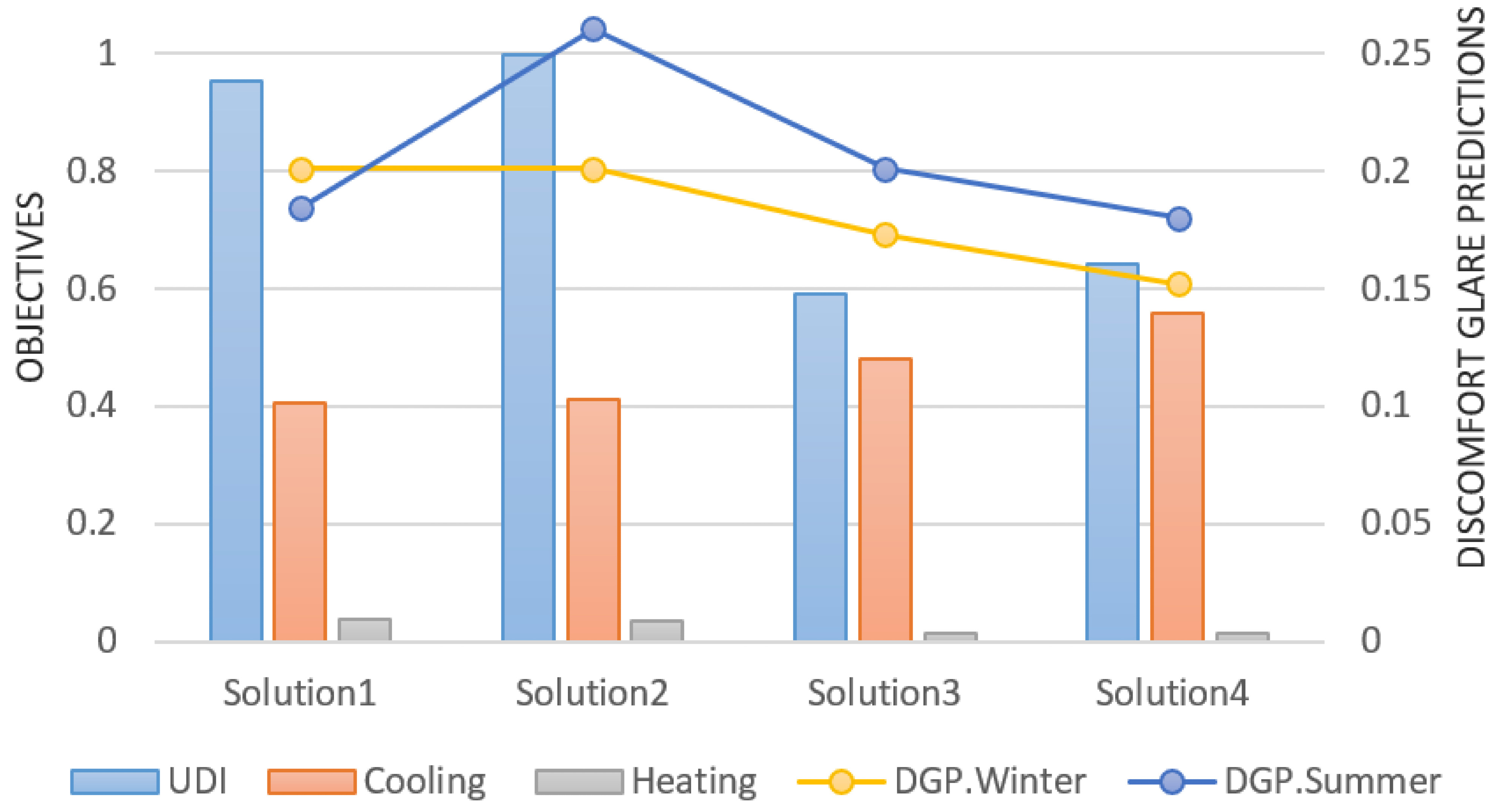 Figure 12
Figure 12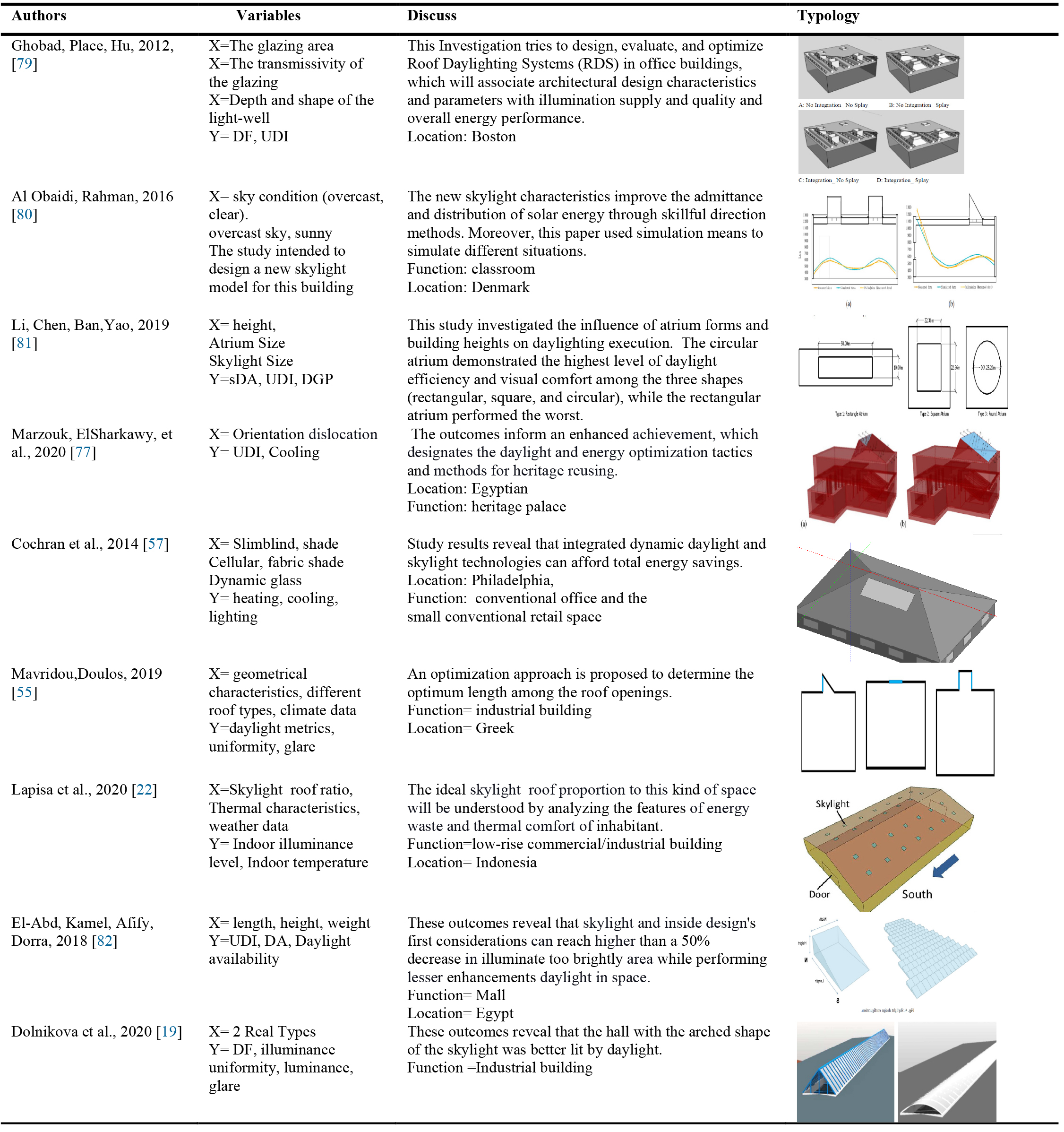 Table 1
Table 1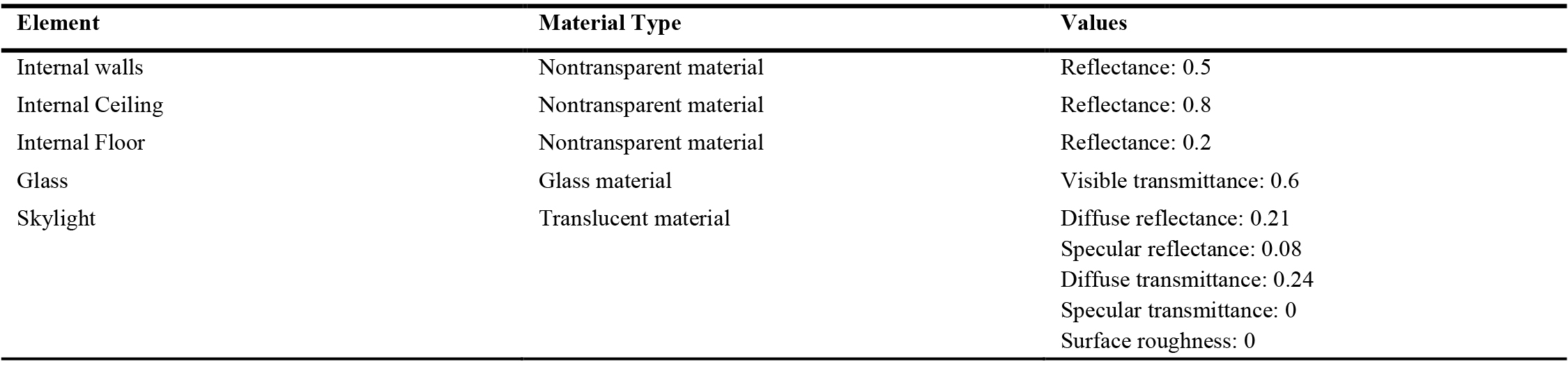 Table 2
Table 2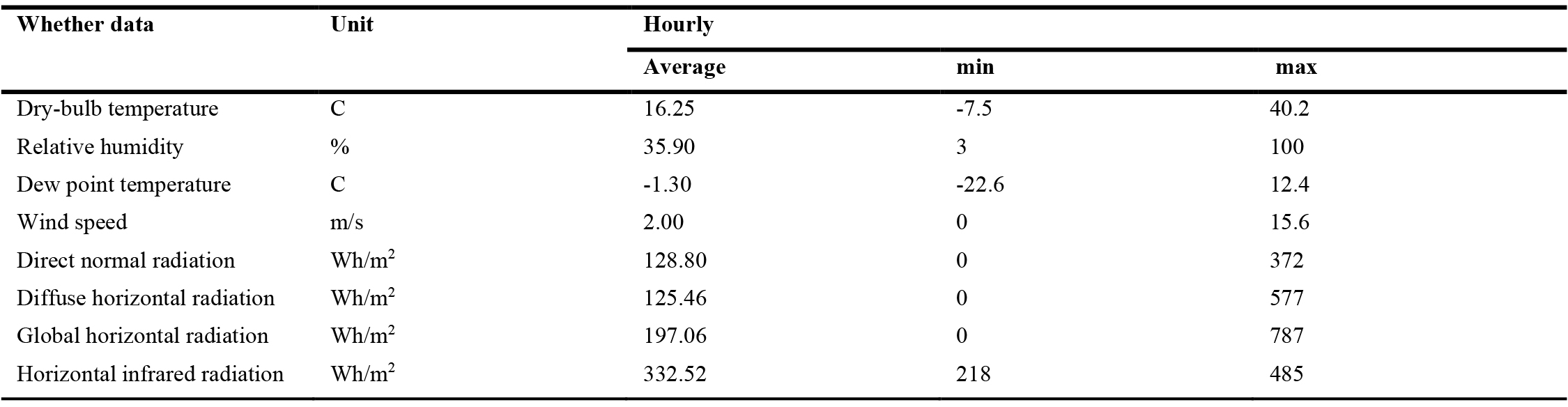 Table 3
Table 3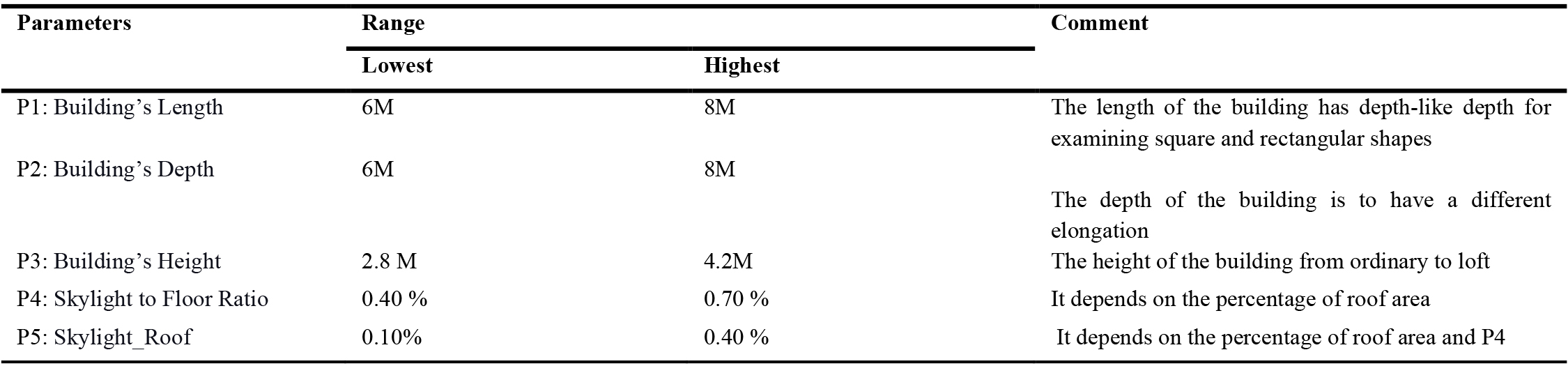 Table 4
Table 4 Table 5
Table 5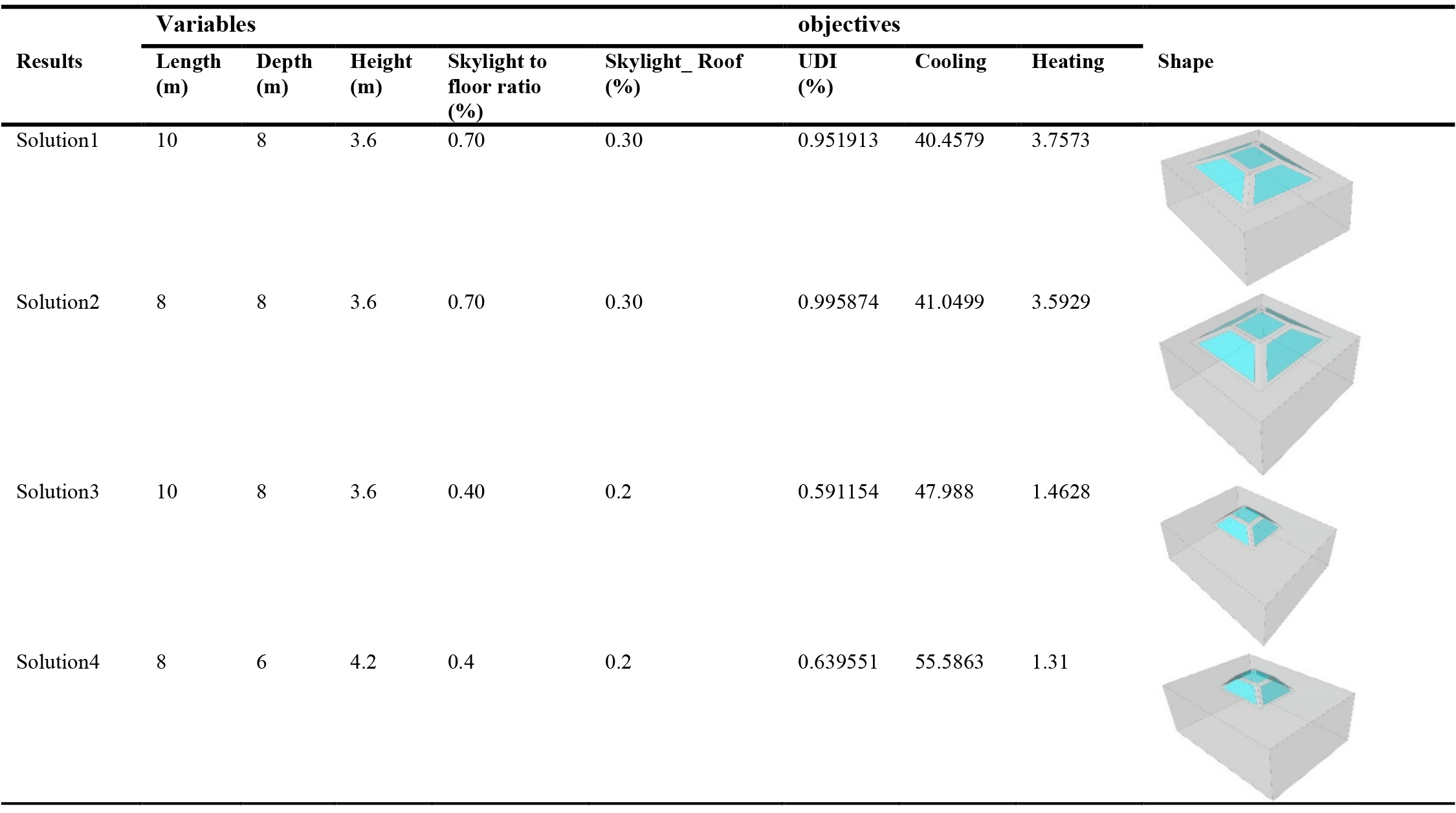 Table 6
Table 6 Table 7
Table 7


