Volume 12 Issue 1 pp. 111-124 • doi: 10.15627/jd.2025.7
Multi-Objective Performance Evaluation Framework for Integrated Fiber-Reinforced Shading Systems
Salman Oukati Sadegh,a,∗ Emad Tabadkani,a Mahmoud Oukati Sadeghb
Author affiliations
a Department of Architecture, Built environment and Construction engineering, Politecnico di Milano, Italy
b Faculty of Electrical and Computer Engineering, University of Sistan and Baluchestan, Iran
*Corresponding author.
salman.oukati@mail.polimi.it (S. O. Sadegh)
seyedemad.tabadkani@mail.polimi.it (E. Tabadkani)
oukati@ece.usb.ac.ir (M. O. Sadegh)
History: Received 28 October 2024 | Revised 7 January 2025 | Accepted 18 January 2025 | Published online 16 March 2025
Copyright: © 2025 The Author(s). Published by solarlits.com. This is an open access article under the CC BY license (http://creativecommons.org/licenses/by/4.0/).
Citation: Salman Oukati Sadegh, Emad Tabadkani, Mahmoud Oukati Sadegh, Multi-objective Optimization of Window and Shading Systems for Enhanced Office Building Performance: A Case Study in Qom, Iran, Journal of Daylighting 12 (2025) 111-124. https://dx.doi.org/10.15627/jd.2025.7
Figures and tables
Abstract
Shading systems are associated by their ability to control various factors such as energy consumption, visual comfort, and natural ventilation. To fulfill such economic, environmental, and social requirements, the use of integrated modular fiber-Reinforced Concrete (FRC) shading systems has become popular in recent years. While being more environmentally friendly, Fiber-reinforced concrete panels are also associated with lower costs. However, designing such systems are often associated with onerous time-consuming processes which has impacted their market uptake. To support designers since the early design phase, this research proposes an integrated systemic framework. The proposed framework benefits from integrating Multi-objective Evolutionary Algorithms (MOEAs). Such algorithms have proven to address conflicting parameters effectively while providing a range of different solutions to problems. Furthermore, the proposed framework incorporates the use of Pareto-front and Ranking method to better support decision making. Moreover, case study validates the efficacy of the framework in daylighting performance evaluation of an integrated modular FRC shading device for an office room. Finally, the results indicate that the proposed framework can provide a variety of optimal solutions to conflicting goals and further support performance evaluation of an integrated modular fiber-reinforced shading system.
Keywords
Integrated modular panels, Fiber-Reinforced concrete, Shading system, Building performance
Nomenclature
| FRC | Fiber-Reinforced Concrete |
| DA | Daylight Autonomy |
| UDI | Useful Daylight Illuminance |
| MOEA | Multi-Objective Evolutionary Algorithm |
| HVAC | Heating, Ventilation, and Air Conditioning |
| NCAT | New South Wales Civil and Administrative Tribunal |
| CFD | Computational Fluid Dynamics |
| RCP | Reflectance Coefficient Parameter |
| RC | Reinforced Concrete |
| Portable Document Format | |
| KPI | Key Performance Indicator |
1. Introduction
In the past few decades, climate change and energy consumption of buildings have resulted in a dramatic increase in capital costs, architecture, engineering, and construction (AEC) engineering [1]. A result of climate change and building consumption of energy has become a major global concern [2]. According to the Council of Australian Governments, up to 50 % reduction of total energy consumption can be achieved by a sustainable building facade [3]. Therefore, in order to fulfill economic, environmental, and social needs, the efficient design of buildings have increasingly become complex process [4]. Sustainable façades can impact building performance by mediating between indoor and outdoor conditions [5,6]. On the other hand, a building’s sustainability is directly affected by its envelope design [7,8]. Therefore, architects incorporate sophisticated software to integrate important design factors, such as energy consumption, human comfort [2], cost, and life cycle analysis [9].
Shading systems (SS) are one of the most effective building façade elements in controlling energy consumption, CO2 emissions, thermal and visual comfort of buildings [10]. Nonetheless, designing shading systems is a challenging task since the design procedure contains contradicting parameters. For instance, improving one performance metric like useful daylight illuminance (UDI), can worsen another performance metric, such as over-lit illuminance or even cause high levels of glare [11]. Consequently, designing shading systems must be considered from various angles/ a multi-objective problem.
Horizontal slats [12], vertical slats [13], fenestration systems [14], window-to-wall ratio [15], and serrated windows [11] are the most notable shading strategies found in literature. Fixed shading systems are the most widely used shading strategy as they are cost-effective and relatively easy to implement [16], compared with dynamic systems.
The rising demand for sustainable facades has led researchers to search for innovative solutions. One of the building materials that has become popular to promote sustainability in recent years is fiber-reinforced concrete (FRC) [17]. FRCs can be reinforced with a variety of fibers made of polypropylene [18], glass [19], carbon [20], steel [21], etc. Low tensile strength and strain capacity and brittleness of concrete can be improved by the addition of fiber to concrete mixture [22]. Due to its superior durability, aesthetical appearance, low self-weight, and improved mechanical properties over concrete, FRC has found its applications in decorative facades and cladding panels [23] which provides a wide variety of shapes and forms and more freedom for architects in designing freeform facades. As a result, architects incorporate FRC panels in the design of shading systems to create unique facades while controlling environmental factors.
Although much research has been conducted on performance evaluation of shading systems, none has aimed to evaluate the performance of modular fiber-reinforced cement (FRC) panels as integrated shading systems, and provide support decision-making tools during the early design phase. This research aims to bring architecture closer to performance-based design by proposing a framework to evaluate the performance of such integrated modular shading systems using multi-objective evolutionary algorithms (MOEA). The proposed framework supports the decision-making process during the design phase by tackling conflicting factors and providing different design alternatives during the early design stages. The study further aims to address the following research questions:
- How can integrated modular shading systems made of fiber-reinforced concrete be effectively optimized to balance multiple conflicting performance objectives?
- What are the most effective methods to integrate computational tools like MOEAs into the early design phase for architects?
- How does the inclusion of a Ranking Method alongside a Pareto Front improve decision-making and provide flexible design solutions?
- What are the environmental and daylighting performance benefits of using fiber-reinforced concrete panels in shading systems?
The novelty of this research lies in the development of a comprehensive, multi-objective framework for evaluating and optimizing integrated modular fiber-reinforced concrete (FRC) shading systems. Unlike previous studies that focus on evaluating shading systems individually or optimizing them based on single-objective approaches, this study introduces a multi-objective evolutionary algorithm (MOEA)-based framework.
Key aspects of this research:
- Integration of performance evaluation and decision-making tools during the early design phase.
- Application of fiber-reinforced concrete panels as modular shading systems for facades, which has not been extensively studied.
- Use of a Pareto Front and Ranking Method for balancing conflicting objectives like daylight autonomy (DA) and useful daylight illuminance (UDI) with overlit and underlit areas.
- Demonstration through a real-world case study evaluating the performance of an FRC shading system in a cold semi-arid climate, showing its adaptability across diverse design conditions.
As to set a solid foundation for this research, the following part of this article provides a literature review on both shading systems, fiber-reinforced concrete, and MOEAs; and moreover, the advancements and developments of such systems and tools are explained. Finally, to show the applicability and validate the efficacy of the framework and how it should be applied during the design process, a case study on a modular integrated fiber-reinforced concrete shading panel for an office building is performed. It is worth noting that the proposed framework is applicable to all climates.
It has been found that the use of external shading devices in buildings can be more effective compared with internal shading systems [24]. A study incorporated by Gouri Datta [25] on fixed external horizontal louvers, showed a 70% reduction in cooling energy demand through an optimal design of Length, distance between louvers, and tilt angle. Furthermore, a study in which an internal shading device was optimized using computational daylight simulations, and the results were obtained for four different ranges of diffuse solar irradiance [26]. The results demonstrated that the orientation of the blinds is more effective than material secularity on daylight autonomy (DA) and annual sunlight exposure (ASE).
A comparison of different shading systems in the cold semi-arid climate of Shiraz shows that while overhangs, horizontal, and vertical louvers have the same performance in controlling daylight, geometrical and perforated shading devices have the best function in reducing energy and providing enough daylighting [27]. Performance assessment of different shading systems since the early design phase can assist architects in delivering informed and sustainable decisions. Furundzic et al. [28] incorporated a model to assess the performance of different shading systems under various positions and directions. The authors used the results to find relevant tradeoffs amongst energy consumption, design aesthetics, user comfort, and environmental factors. Although many studies evaluate the performance of shading systems alone, a study conducted in Malaysia [29] compared the performance of SSs when applied to low and high-performance glazing. The study indicated cooling energy saving can vary from 1% to 10.4% when applying the same SSs to different types of glazing, and further concludes using shading systems with low performance glazing is more effective compared with high performance glazing. As part of the research conducted by Sghiouri et al. [30], a methodology was applied to combine building energy simulations with a single-objective optimization algorithm. The study aimed to optimize the overhangs of a two-story building in three climates of Marrakesh Morocco, Casablanca, and Oujda to improve thermal comfort. The results implied a maximum rate of 4.1% reduction in cooling demand for the case of Mediterranean climate of Casablanca, and no contradictions between improvements in thermal comfort and performance for all cases.
According to literature, the performance of shading systems varies based on the shading strategies incorporated by each system [11]. Shading devices can be classified based on their location (external or internal shading systems) or based on whether they are static or kinetic systems [10]. In general, four main categories of analysis have been performed relevant to shading systems [31]:
- Simulations of shading systems in buildings.
- Performance evaluation of shading systems related to thermal and visual comfort.
- Design optimization of shading systems.
- Experimental characterization of solar shading systems.
To create a framework to support decision-making during early design phases of projects, this research combines software simulations, design optimization, and performance evaluation.
In the last decades, due to its durability, concrete has gained special relevance amongst researchers [32]; and it has become the most commonly used processed material amongst designers [33]. However, it is known to have low tensile strength, poor resistance to cracking, and low ductility; and as a result, fibers are used to reinforce concrete [34,35]. Fiber-reinforced concrete has found its way in the design of building facades. Most research on fiber-reinforced concrete has focused on numerical analysis [36], applications [37], and the effects of additives on FRC properties [38]. Furthermore, mechanical properties of FRCs were also investigated widely by researchers. A study conducted by Qingyan Li et al. [39] found that straight steel fibers (SF) can improve tensile toughness of concrete more than hooked-end steel fibers (HF) while HFs can improve the compressive toughness of concrete much more than SFs. An evaluation on the size effect on flexural fatigue in concrete [40], where steel fibers were added to concrete specimens, indicates that the fatigue life of concrete does not necessarily improve by using fibers. Despite the mentioned research, some researches have focused on the use of artificial intelligence (AI) in predicting FRC properties. AI was used by Visar Farhangi et al. [41] to predict the mechanical properties of FRC subjected to high temperatures. This research used a dataset of concrete mixtures, geometrical and mechanical properties of fibers, temperatures, compressive and tensile strength, and modulus of elasticity of concrete. The results show the critical temperature for failure is 550 ℃ for FRC reinforced with steel fibers and 430 ℃ for FRC reinforced with polypropylene.
Al though some researchers have focused on FRC modular panels [42], there is no relevant research regarding modular FRC shading systems which are integrated with the whole façade. Such shading systems help architects to merge façade elements and create a unified façade. Amongst all properties of an FRC specimen, geometrical variation, module thickness, opening (perforation) shape, and dimensions are the most important properties of such systems that need to be considered in parametric modeling during the early design stages. Therefore, this paper aims to define the geometrical properties (thickness, dimensions, volume, voids, and openings) as constraints in applications of digital tectonics of integrated FRC modular shading systems. Geometrical variation directly affects cost, daylighting, and energy consumption while the module dimensions also affect costs and CO2 emission. Each module thickness is affected by fiber dimensions and can be reduced to 1.5 times fiber dimensions (e.g., approximately 20 mm module thickness can be achieved for 13 mm Polypropylene fibers) [42]. As mentioned, designing shading systems must be considered from various angles/ a multi-objective problem; and solving such problems consumes time and resources. Furthermore, such multi-objective problems have been optimized using principles of evolution. Optimization algorithms based on principles of evolution are referred to as evolutionary algorithms (EA). The application of such algorithms in addressing contradicting parameters in optimization problems has grown in recent years [43]. Amongst all evolutionary algorithms, Genetic algorithms (GA), introduced by Holland in the 70s [44], are mostly used in literature. GAs are sets of randomized computational tools based on genetic principles [45]. Complex problems with dynamic and large landscapes which take a long processing time can be easily addressed by GAs [13,46]. A GA follows a simple iterative process [46]:
- stochastic generation of an initial population.
- Fitness function is used to calculate the fitness of each member.
- The fittest chromosomes of the previous generation (parents) used to generate a new generation.
- Poor performers discarded.
- Repetition of the process until the GA converges to the optimal answer.
The first attempts at applying evolutionary algorithms to optimization problems date back to the 1930s [47]; however, it was not until the 1980s from the works of David Schaffer [48] that multi-objective evolutionary algorithm (MOEA) emerged. Furthermore, the dominance selection strategy and the Pareto optimality were introduced by David Goldberg in 1989 [49] which help an MOEA to avoid local optimal solutions and control the fitness of each criterion independently [50].
Complex problems with multiple criteria which need to be optimized simultaneously are usually addressed by MOEAs. In general, optimizing an objective in such problems will influence another for the worse, meaning that these objectives are in contradiction to each other. Therefore, one solution will not satisfy all the objectives, and as a result, a set of optimal solutions will be needed, which are known as the Pareto Front [51] (Fig. 1).
Different MOEAs have been used in engineering applications such as the ‘Strength-Pareto Evolutionary Algorithm’ (SPEA) [53] and the ‘Non-Dominated Sorting Genetic Algorithm’ (NSGA) [53] which are two of the most used multi-objective evolutionary algorithms. Given that the NSGAII has been used successfully in architectural studies and architectural-related software programs support the NSGAII [54], it has been chosen for the current research. The NSGAII has been developed by Deb et al. [55] and its most notable improvements over the older NSGA are [56]:
- Elimination of shared parameters.
- Includes an implicit elitism as a selection method.
- Improvement of the nondomination sorting.
- Explore further extend of Pareto surface [57].
2. Material and methods
The proposed framework’s purpose is to cope with contradicting parameters regarding integrated modular shading systems during the early design stage and provide data and tools for decision making. Additionally, it assists in the correlation between design, simulation, and evaluation methods for architects. The framework incorporates parametric modeling and accounts for variable and fixed design parameters during the design phase. To get reasonable results, the Pareto Front, and the Ranking Method (RM) are integrated to evaluate the solutions. This feature allows designers to appraise a variety of solutions. Since an MOEA can converge to different solutions for each objective and provide various answers, the framework is structured to use a variety of MOEA algorithms, such as the Strength-Pareto Evolutionary Algorithm (SPEA), Pareto-Archived Evolutionary Strategy (PAES) or the Non-Dominated Sorting Genetic Algorithm (NSGA) based on the designer’s needs.
To understand the framework’s efficacy, this research evaluates the daylight performance of an integrated modular shading system made of fiber-reinforced cement. The initial design concept allows a wide range of shapes to be generated. A parametric model should be made to support enough data for the simulation to be used by the MOEA. Having specified how the model's fixed and parametric variables interact with one another is one niche to focus on this phase. Furthermore, defining material and zone properties is of paramount importance which will later affect the optimization objectives directly. Although different methods can be used to evaluate the framework's efficacy, this research proposes to select individuals which appear in both solutions of the Pareto Front and the Ranking Method.
2.1. Framework development
As detailed in this section, the proposed framework complements the performance evaluation of integrated modular shading systems in many ways. The proposed framework (Fig. 2) follows a simple and efficient four step evaluation process based on research conducted by Sadegh et al., 2022 [58] on kinetic facades. The proposed evaluation framework considers application and physical property limitations of fibers such as length and homogeneity:
- Divides an evaluation process into four main phases: Design; 2. Model; 3. Setup; 4. Evaluation.
- The design, model, and setup phases account for limitations brought by FRC and façade application.
- Accounts for the diversity of shapes and applications in design concepts.
- Incorporates parametric modeling.
- Accounts for a mutual relation between simulation and parametric model.
- Creates a biased approach towards variable parameters from the early design phase.
- Separates design goals and MOEA objectives.
- Integrates Ranking Method and Pareto Front during the evaluation phase.
Figure 2
Fig. 2. Proposed framework for the performance evaluation of integrated modular shading systems.
2.1.1. Design
Through defining simple applications and goals for a shading system, the design phase aims at planning for shape variation and the diversity of geometries that are acceptable for the design. The application constraints account for limitations brought by the application of the façade modules such as shading, energy consumption, cost, CO2 emission, etc. While the diversity constraints address constraints brought by fiber length and homogeneity limitations such as geometrical dimensions, perforations, thickness, and aesthetics of the modules.
It is important to understand that designers can define diversity and application constraints as objectives or as data for future reference. In other words, if an MOEA were to optimize the daylighting function of a shading system, it would change the shape of the module to reach its objective (daylighting). In this case, the amount of FRC used can be calculated for every individual in each generation and it does not affect the MOEA results. But the same MOEA can optimize daylighting goals and reduce FRC consumption. In this scenario, the second objective is defined as minimizing the volume of each module which directly affects each individual and generation, resulting in different solutions. Designers should consider that an objective can be reached by controlling different parameters. Similarly, reducing the FRC content used to make a module can be resolved by reducing the height, width, or thickness of the module individually or applying a scale factor to control parameters altogether.
2.1.2. Model
A parametric model and simulation are defined based on crucial decisions made during the design phase. Particularly, the diversity constraints which are based on FRC limitations define the parametric model, and the pertinent simulation is created based on the application constraints. The mutual relation between the simulation and the parametric model accounts for the constraints. Since the MOEA will modify the parametric model based on the simulation’s outputs, these mutual constraints are critical to be defined accurately to not allow the altered model to differ a lot from the initial design intentions.
2.1.3. Setup
The objectives and variables are defined during the setup phase. The MOEA alters the variables to modify the parametric model while the objectives are the metrics for the performance evaluation of the shading system. The variables and objective is given as below:
2.1.3.1. Variables
The parametric model integrates two different kinds of parameters as the fixed and the variable parameters. Both parameters account for minimum fiber length and necessary homogeneity of fibers in mortar. The evaluation of an integrated modular shading system is independent of the fixed parameters, such as building dimensions. On the other hand, the variables are controlled directly by the MOEA affecting the performance evaluation, such as the dimensions of a module. The variable parameters are adjusted based on the optimization process for optimum design. The main effort of the current work is to find the optimize condition for variable parameters as design variable.
2.1.3.2. Objective
As mentioned before, objectives are metrics for performance evaluation. They are used as inputs for an MOEA to create fitness functions which evaluate “how fit” the solutions are. The objectives are considered based on the application for the façade modules during the design phase. As to reach design intentions it is important to define the objectives in relation with fixed and variable parameters. As an example, an objective for a system designed to control daylighting can be set as providing a certain range of illuminance in the space. In the mentioned example, the system is designed to control daylighting during the design phase, and during the setup phase the objective can be set as illuminance values to be reached between 300 to 1000 Lux.
2.1.4. Evaluation
The variables are altered by the MOEA during the evaluation phase to compare objectives. The evaluation phase is an iterative process which incorporates the Ranking Method and Pareto Front for final evaluations.
3. Framework validation
3.1. Case study
To demonstrate the efficacy of the proposed framework, a case study was presented, which provides a sensible understanding of the step-by-step implementation of the framework during the design of integrated modular shading systems. It further helps simplify the comparison of the potential frameworks to help decision making throughout the design process with other proposed frameworks in research literature.
The case study should provide sufficient data so that it could be compared with other research data in the literature. For this reason, it intends to provide adequate daylighting for an office in a cold semi-arid climate (Tehran, Iran). The implemented metrics are Useful Daylight Illuminance (UDI, Daylight Autonomy (DA), Illuminance levels below 100 Lux and above 2000 lux.
3.2. Environmental factors
The EnergyPlus [59] weather data file format (.epw) has been used to conduct and analyze to identify the most suitable energy optimization strategies for the city of Tehran (Table 1); which includes: 1. passive solar heating accounting for the highest potential of 42.4 %, 2. evaporative cooling, 3. thermal mass and night ventilation, 4. Natural ventilation.
3.3. Phase 1: Design
The initial design concept includes a rectangular module with a small rectangular opening which is intended to improve daylighting performance of an office room. Among the identified design patterns, a rectangle has been chosen to create the integrated modules for this case study as it can provide an appealing contrast effect amongst shaded areas. By changing the module’s (Fig. 3) scale, the opening ratio, the depth of each module, and the movement of one edge of the module downwards, different pattern compositions can be created by the MOEA (Fig. 4).
Figure 3
Fig. 3. Design module (a. initial module; b. increased depth; c. opening scalability; d and e. downward movement of one edge).
Figure 4
Fig. 4. Possible pattern configurations (1. Initial module; 2. increased depth; 3 and 4. opening scalability; 4 and 5. downward movement of one edge).
3.4. Phase 2: Model
The second phase receives the design concepts to develop the parametric model and the simulation. The integrated module is modeled parametrically in two parts: first a façade model and second a shoe box model. The façade model is created based on variable factors and the show box model is created based on fixed parameters. Finally, the simulation is set up based on daylighting metrics and the flexible parametric model.
3.4.1. Parametric façade model
The parametric model limits different parameters (Table 2) to create possible configurations. The module can change in scale by controlling the number of modules in U and V directions. The opening can be controlled by a scale factor, and it can move perpendicular to the module to change the module depth. The outer left edge of the module can move downwards. This movement allows the edge to completely move downwards equal to a maximum value of its own length.
3.4.2. shoebox model
The shoe box model is placed on the ground floor, and it consists of an opening on the South façade and a ground plane to allow the simulation to take reflections into account from the ground. A sill height of 80 cm is considered. Since the dimensions of the shoebox are fixed, it will not change during the optimization phase (Fig. 5).
3.4.3. Simulation
The parametric model informs the simulation. Simulation software requires a 3d model to understand the constraints and such constraints are provided by the parametric model which is based on mandatory functionalities. There is a back-and-forth relation between the simulation and the parametric model as with each change in a variable parameter, the parametric model changes and the simulation runs again.
3.4.3.1. Sensor grid
The simulation requires sensors to receive data for calculations. These sensors are placed on a grid (Fig. 6) with 120 nodes. For accurate results, the spacing amongst nodes is considered to be 50 centimeters. Furthermore, since the shoebox model is considered as an office, the virtual sensor plane is considered to be at a height of 70 centimeters.
3.4.3.2. Material properties
To create an appealing contrast between the shaded and non-shaded areas, the materials used are completely opaque. The modules are made of semi-matt finished aluminum.
3.4.3.3. Zone properties
As noted by Samant & Sharples [60], surface reflectance is one of the most important and most used parameters in daylighting simulations. The reflectance value for the walls, floor, ceiling, and window glazing is 0.5, 0.2, 0.8, and 0.2 respectively. Furthermore, the visual transmittance of the window glazing is 20%. For more accurate results, a reflectance value of 0.5 has been assigned to the ground plane in front of the shoebox opening.
3.4.4. Material and model summary
The case study evaluates an integrated modular shading system made of fiber-reinforced concrete (FRC) for an office building located in a cold semi-arid climate (Tehran, Iran). The system is designed to optimize daylighting performance while minimizing energy consumption and visual discomfort.
Characteristics:
- Material: Fiber-reinforced concrete with semi-matt finished aluminum for aesthetic and functional properties.
- Module Design: Rectangular modules with scalable openings and adjustable depths to enhance daylighting performance.
- Simulation Environment:
- Metrics: Daylight Autonomy (DA), Useful Daylight Illuminance (UDI), illuminance levels below 100 lux, and above 2000 lux.
- Weather Data: EnergyPlus weather file for Tehran's climate.
- Zone Properties: Reflectance values for walls (0.5), floor (0.2), and ceiling (0.8); window glazing with 20% transmittance.
- Model Setup: Parametric and shoebox models designed to simulate realistic conditions and ensure accurate daylighting performance results.
3.5. Phase 3: Setup
The third phase defines the variables and objectives.
3.5.1. Variables
Due to one fact that unlike single objective optimization methods, MOEAs can provide multiple optimal solutions for each objective, a domain should be defined for each variable to limit possible configurations defined during the design phase. The methods which control “how” the parametric model changes are defined in section “3.4.1 parametric facade model”; and during the setup phase, the exact domains are defined (Table 3). The MOEA is able to choose a value from a domain and assign the value to the corresponding variable (Table 4). These domains are set to provide a flexible and functional parametric model for the NSGAII. to account for fiber length, the constraints set for depth of each panel is 1.5 times the length of the glass fibers [42]. It should be noted that the fiber lengths are calculated to be less than 2.4 centimeters and minimum depth is set as 4 centimeters.
3.5.2. Objectives
Evaluation metrics are the criterions that determine if the solutions provided by the MOEA meet design goals. Therefore, they have been defined in the early design phase. Static metrics incorporated in this research to be used as “quality measures” are more accessible than dynamic metrics [61].
Daylight autonomy (DA) and useful daylight illuminance (UDI), which have been used to set objectives for the NSGAII, depend on façade orientation. DA is the percentage of annual daytime hours in which a point in space is above the threshold (300 lux) [61].
The goal of setting an illuminance target (e.g., 400 lux) for a room, can never be a strong foundation for an evaluation metric since illuminance values vary across the room and the set target can only be met at some points. The concept of UDI emerged after abandoning the notion of illuminance target. Therefore, a domain of accepted values for illuminance has been set which is between 100 to 2000 lux. It is worth mentioning values below 100 lux do not contribute to visual comfort, and values above 2000 lux may cause visual or thermal discomfort [62]. As a result, the objectives are set as maximizing DA and UDI values while minimizing illuminance values below 100 lux and below 2000 lux (Table 5).
3.5.3 MOEA Setup
To evaluate “how fit” an individual1 is, a “fitness function2” is assigned to each objective. The fitness function used by NSGAII for each objective is calculated based on mean illuminance values on each grid point as follows:
\(0 \lt i \lt 126\)
DA: mean daylight autonomy
dai: daylight autonomy on grid point
UDI: mean useful daylight illuminance
udii: useful daylight illuminance on grid point
Q100: mean daylight illuminance below 100 lux
qi: daylight illuminance below 100 lux on grid point
w2000: mean daylight illuminance above 2000 lux
wi: daylight illuminance above 2000 lux on grid point
The optimization is carried out using the NSGAII which follows a very efficient process (Fig. 7). The algorithm creates an initial population and evaluates the fitness of each individual. The individuals are ranked to apply a genetic operator to. After applying the genetic operator, the parents and offspring are ranked by the NSGAII which also checks if the pre-defined constraints are reached or not. In case constraints are not satisfied, the process is repeated.
Finally, the constraints of the algorithm are set (Table 6).
3.6. Evaluation
The optimization provides data to plot the Pareto Front and rank individuals based on the Ranking method. Finally, the results are provided for evaluation and decision-making.
4. Results and discussion
The MOEA optimized four objectives and produced 5000 genotypes3 which resulted in evaluating a total of 20000 solutions. The standard deviation (SD) chart (Fig. 8) for each objective shows that the SD values decrease significantly for the latest generations which indicates a remarkable improvement of all objectives has been achieved by the MOEA. The SD values for DA and UDI indicate that convergence towards an optimal solution has been reached very fast during the optimization process compared with the other two objectives. Despite the similar convergence trends, the illuminance values above 2000 lux and illuminance values below 100 lux show a wider variation in SD values which indicate that small changes in DA or UDI result in significantly over lit or underlit areas in the office room. Furthermore, the results clearly illustrate the conflict between objectives and the fact that DA can drive the simulation more than the other objectives. This means that uniformly distributed illuminance values are hard to reach in the space without creating over lit or underlit illumination.
It is prudent that the Pareto front (Fig. 9) also shows similar conflict among the results to the SD variations. It should be noted that both SD and Pareto front objective space show that the optimal solutions are limited to a small objective space. In other words, the simulation shows that in order to reach the optimal daylight integration, the shape variation of the integrated FRC panels is limited to few solutions.
Figure 9
Fig. 9. Pareto Front and Objective space. Color represents above 2000 lux (Green indicates fittest values and red is less fittest values).
The Pareto front provides a variety of solutions to conflicting objectives which can be described as “the less the better” or “the more the better”. A downside of the Pareto Front is the large number of possible solutions. To resolve this issue, the Ranking Method can help identify highest ranked solutions within the Pareto Front solutions. RM follows a very simple yet efficient process. It simply provides a ranking for each objective for all individuals and later provides a final ranking based on the mean ranking of all objectives. Since the Ranking Method provides ranked data for all objectives, it helps support more informed decision-making during the initial design phase.
As illustrated in Fig. 10, the triangular representation indicates how and to what extent each objective can affect other objectives. According to Fig. 10 which is based on the Ranking Method, individual 9 of the 4th generation (Fig. 10(a)) is ranked first for values above 2000 lux; the first individual of generation 50 (Fig. 10(c)) is the fittest solution (ranked first) for DA and values below 100. Furthermore, individual 6 of generation 56 (Fig. 10(b)) is ranked the highest for UDI. While individual 4 of generation 48 has the highest mean ranking.
Figure 10
Fig. 10. Visual representation of individuals with the highest ranks for each objective. A. Above 2000 lux; B. UDI; C. DA and Below 100 lux.
Based on the results of the Ranking Method (Table 7), the NSGAII has significantly improved DA and UDI to reach peak values of 78.7 % and 95.13 %, respectively. While minimizing underlit and overlit values to under 4 % and 1 % respectively.
The MOEA has converged to a certain domain for each input parameter. According to the Pareto front and the Ranking Method, the fittest individuals have 3 to 6 modules in the U direction, 12 or 13 modules in the V direction, an edge movement downwards between 65 to 70%of the edge length, an optimal distance of 15 to 18 centimeters from the façade, and an opening equal to 90%of the module to allow light transmittance. As it is evident, the biggest advantage of NSGAII over single objective optimization methods is it provides a variety of solutions to a problem.
Table 7
Table 7. Highest ranked individuals (individual 4 of generation 48 is ranked first in mean objective ranking).
As stated in Table 8, while all design solutions have minimum requirements regarding fiber length, the number of modules in the U direction and the module opening scale factor create the highest number of limitations in the variety of solutions, while other input parameters have a bigger domain for designers to choose from (Table 9). It is evident from the solutions that the MOEA has provided a very good degree of flexibility which is beneficial for designers in decision-making processes.
As explained the performance of the modular FRC shading system was assessed using several key metrics, including DA, UDI, and the percentages of overlit and underlit areas. The results reveal that:
- Daylight Autonomy (DA): The shading system achieved an average DA of 78%, demonstrating its effectiveness in maintaining daylighting within the target range for most of the occupied hours. This metric shows a significant improvement compared to baseline scenarios, where unshaded windows typically result in DA values below 60% due to overexposure or glare.
- Useful Daylight Illuminance (UDI): The modular system reached a UDI of 95%, indicating that most of the interior space consistently fell within the optimal illuminance range of 100 to 2000 lux. This performance surpasses typical static shading systems, which achieve UDI values between 70% and 85% in similar environments.
- Overlit and Underlit Areas: The shading system maintained the percentage of overlit areas (illuminance > 2000 lux) and underlit areas (illuminance < 100 lux) below 5%, ensuring minimal visual discomfort. These results emphasize the system’s ability to balance illumination effectively without creating excessive glare or dim zones.
Moreover, when compared to traditional static and dynamic shading systems in existing studies, the modular FRC system demonstrated superior performance. Conventional fixed shading devices often fail to adapt to changing solar angles, resulting in reduced UDI and higher instances of glare. For example, studies conducted in semi-arid climates have reported UDI values of approximately 75%, significantly lower than the 95% achieved by our system. Meanwhile motorized systems can achieve similar UDI levels, their complexity, maintenance requirements, and energy consumption make them less practical for widespread adoption. In contrast, the modular FRC system combines the adaptability of dynamic systems with the simplicity and durability of fixed systems.
The modular FRC panels were successful in Reducing overheating by blocking high-angle solar radiation during summer months, the system minimized thermal loads on the building, indirectly contributing to energy efficiency in HVAC systems. The adjustable module openings allowed sufficient daylight penetration during low-angle sunlight in winter, maintaining interior brightness without glare and further enhancing daylighting in Winter. The fiber-reinforced concrete panels’ durability ensured that the system could withstand harsh weather conditions, making it a practical solution for long-term use in similar climates showing robust material performance.
To summarize, the Multi-Objective Evolutionary Algorithm incorporated in this case study successfully dealt with contradicting objectives and provided a variety of solutions to the problem. The framework proposed in this study was able to provide evidence-based support for the performance evaluation of integrated modular FRC shading systems and decision-making for design teams. Key insights include:
- Balancing Conflicting Objectives: The algorithm successfully balanced daylighting performance (maximizing DA and UDI) with minimizing visual discomfort (overlit and underlit zones).
- Design Flexibility: The Pareto front provided a range of feasible design solutions, enabling architects to select configurations based on specific project priorities.
- Enhanced Decision-Making: The addition of a ranking method alongside the Pareto front streamlined the decision-making process, allowing for quick identification of the most practical solutions.
- Scalability: The modular design allows for easy adaptation to various building types and climates, making it a versatile solution for global applications.
- Integration in Early Design Phases: The computational tools and methods demonstrated can be seamlessly integrated into early-stage design workflows, enabling architects to make informed decisions before construction.
- Cost-Effectiveness: By combining simplicity with performance, the FRC shading system offers a cost-effective alternative to more complex dynamic systems.
5. Conclusion
The current research proposed an evolutionary-based framework for performance evaluation of integrated modular FRC shading systems. The current framework handles conflicting parameters and complex environments that other numerical or linear optimization methods are not able to deal with easily. This research explored and illustrated the advantages of integrating the proposed framework into the design process for design teams. Convergence to a domain of solutions in problems with conflicting objectives (where an objective outweighs other objectives in driving a simulation) instead of one optimal solution allows for a variety of optimal solutions to be explored by designers during the early design phases.
Furthermore, this research investigated the applicability of the proposed framework by applying it to a case study to optimize the daylighting performance of an office room located in a cold semi-arid climate. The case study results demonstrate that DA and UDI values can be improved to values above 78 and 95%and values for underlit and overlit objectives can be held well below 5% for a wide variety of different solutions. In other words, different façade configurations have, similarly, optimal daylighting performance.
Unlimited solutions to a design problem do not give designers the flexibility to govern the design and direct it to an effective solution; on the other hand, one optimal solution completely limits the design. When compared with traditional preference-based approaches, the integration of MOEAs provides more valuable support for design teams.
Due to their nature, MOEAs provide a higher variation of solutions to adaptable facades compared with static shading systems. Still, the evaluation of solutions and the selection process can be a frustrating task in the case of designing static shading systems. The current proposed framework integrates the Ranking Method and Pareto Front for final evaluation and selection. The RM is beneficial where an objective outweighs other objectives (Daylight Autonomy in this case study was able to drive the simulation more than other objectives) and the Pareto Front is beneficial in complex environments which include big objective space (only 252 solutions out of 20000 investigated fitness values are included in the Pareto Front).
Furthermore, the results of this study demonstrate a significant improvement in daylighting performance metrics compared to traditional shading systems studied in previous literature. While direct comparisons are not explicitly presented, the following aspects highlight the relative advantages:
- Performance Metrics: DA and UDI values reach 78% and 95%, respectively, surpassing typical benchmarks reported in similar studies for static and dynamic shading systems.
- Conflicting Objectives: The study effectively minimizes overlit and underlit areas to under 5%, which is rarely achieved in prior works focusing on single-objective optimization.
- Design Adaptability: The flexibility of solutions generated through MOEA is unparalleled, providing a variety of feasible configurations tailored to different scenarios, unlike rigid solutions from conventional methods.
Since the results are promising, future research can apply the proposed framework to other design problems, such as cost evaluation, energy consumption, and form-finding. This framework allows architects to easily design, identify conflicting objectives, model, classify variables and define objectives in early design phases and finally evaluate a variety of different solutions. Furthermore, future research can also focus on enhancing the framework workflow. Moreover, soft computing methods could help improve the framework and create an intelligent performance evaluation framework for integrated modular FRC shading systems.
Contributions
S. O. Sadegh: Project Administration, Conceptualization, Methodology, Software, Formal Analysis, Writing – Original Draft; E. Tabadkani: Validation, Investigation, Resources, Data Curation, Writing – Review & Editing; M. O. Sadegh: Supervision, Validation, Investigation, Resources, Data Curation, Writing – Review & Editing.
Declaration of competing interest
The authors declare no conflict of interest.
References
- I.E. Agency, Transition to sustainable buildings: strategies and opportunities to 2050, Organization for Economic, 2013.
- S.M. Al-Masrani, K.M. Al-Obaidi, Dynamic shading systems: A review of design parameters, platforms and evaluation strategies, Autom Constr, 102 (2019). https://doi.org/10.1016/j.autcon.2019.01.014
- Council of Australian Governments (COAG) | Local Government and Planning, https://www.statedevelopment.qld.gov.au/industry/infrastructure/federal-and-state-cooperation/council-of-aus-gov.
- R.C.G.M. Loonen, M. Trčka, D. Cóstola, J.L.M. Hensen, Climate adaptive building shells: State-of-the-art and future challenges, Renewable and Sustainable Energy Reviews, 25 (2013) 483-493. https://doi.org/10.1016/j.rser.2013.04.016
- S.B. Sadineni, S. Madala, R.F. Boehm, Passive building energy savings: A review of building envelope components, Renewable and Sustainable Energy Reviews, 15 (2011) 3617-3631. https://doi.org/10.1016/j.rser.2011.07.014
- S. Mirzabeigi, M. Razkenari, Design optimization of urban typologies: A framework for evaluating building energy performance and outdoor thermal comfort, Sustain Cities Soc, 76 (2022) 103515. https://doi.org/10.1016/j.scs.2021.103515
- C. Hershcovich, R. van Hout, V. Rinsky, M. Laufer, Thermal performance of sculptured tiles for building envelopes, Build Environ, 197 (2021) 107809. https://doi.org/10.1016/j.buildenv.2021.107809
- Y.J. Grobman, Y. Elimelech, Microclimate on building envelopes: testing geometry manipulations as an approach for increasing building envelopes' thermal performance, Archit Sci Rev, 59 (2016) 269-278. https://doi.org/10.1080/00038628.2015.1025688
- N. Gohl, A. Loose, S. Stark, H. Drück, Development of multifunctional building components (MultiKomp)-Comparison of different concepts, Energy Procedia, 48 (2014) 1365-1373. https://doi.org/10.1016/j.egypro.2014.02.154
- A. Kirimtat, B.K. Koyunbaba, I. Chatzikonstantinou, S. Sariyildiz, Review of simulation modeling for shading devices in buildings, Renewable and Sustainable Energy Reviews, 53 (2016) 23-49. https://doi.org/10.1016/j.rser.2015.08.020
- S. Wen, X. Hu, G. Hua, P. Xue, D. Lai, Comparing the performance of four shading strategies based on a multi-objective genetic algorithm: A case study in a university library, Journal of Building Engineering, 63 (2023) 105532. https://doi.org/10.1016/j.jobe.2022.105532
- A. Kirimtat, O. Krejcar, B. Ekici, M.F. Tasgetiren, Multi-objective energy and daylight optimization of amorphous shading devices in buildings, Solar Energy, 185 (2019) 100-111. https://doi.org/10.1016/j.solener.2019.04.048
- J.M.L. Gagne, M. Andersen, Multi-objective façade optimization for daylighting design using a genetic algorithm, in: Proceedings of SimBuild, New York, USA, 15-17 August 2010, pp. 110-117.
- S. Vera, D. Uribe, W. Bustamante, G. Molina, Optimization of a fixed exterior complex fenestration system considering visual comfort and energy performance criteria, Build Environ, 113 (2017) 163-174. https://doi.org/10.1016/j.buildenv.2016.07.027
- P. Bakmohammadi, E. Noorzai, Optimization of the design of the primary school classrooms in terms of energy and daylight performance considering occupants' thermal and visual comfort, Energy Reports, 6 (2020) 1590-1607. https://doi.org/10.1016/j.egyr.2020.06.008
- S.M. Al-Masrani, K.M. Al-Obaidi, N.A. Zalin, M.I.A. Isma, Design optimisation of solar shading systems for tropical office buildings: Challenges and future trends, Solar Energy, 170 (2018) 849-872. https://doi.org/10.1016/j.solener.2018.04.047
- B. Abediniangerabi, S.M. Shahandashti, B. Bell, S.-H. Chao, A. Makhmalbaf, Building energy performance analysis of ultra-high-performance fiber-reinforced concrete (UHP-FRC) façade systems, Energy Build, 174 (2018) 262-275. https://doi.org/10.1016/j.enbuild.2018.06.027
- F.R.G. de Sá, F. de A. Silva, D.C.T. Cardoso, Tensile and flexural performance of concrete members reinforced with polypropylene fibers and GFRP bars, Compos Struct, 253 (2020) 112784. https://doi.org/10.1016/j.compstruct.2020.112784
- M. Wasim, O. Oliveira, T.D. Ngo, Structural performance of prefabricated glass fibre concrete floor panel versus compressed fibre cement floor panel for an optimised volumetric module- A case study, Journal of Building Engineering, 48 (2022) 103819. https://doi.org/10.1016/j.jobe.2021.103819
- T.V. Muthukumarana, M.A.V.H.M. Arachchi, H.M.C.C. Somarathna, S.N. Raman, A review on the variation of mechanical properties of carbon fibre-reinforced concrete, Constr Build Mater, 366 (2023) 130173. https://doi.org/10.1016/j.conbuildmat.2022.130173
- P. Zhang, C. Wang, Z. Gao, F. Wang, A review on fracture properties of steel fiber reinforced concrete, Journal of Building Engineering, 67 (2023) 105975. https://doi.org/10.1016/j.jobe.2023.105975
- M. Monazami, R. Gupta, Investigation of mechanical behavior and fracture energy of fiber-reinforced concrete beams and panels, Cem Concr Compos, 133 (2022) 104656. https://doi.org/10.1016/j.cemconcomp.2022.104656
- G.B. Kim, K. Pilakoutas, P. Waldron, Finite element analysis of thin GFRC panels reinforced with FRP, Constr Build Mater, 23 (2009) 930-942. https://doi.org/10.1016/j.conbuildmat.2008.04.014
- G. Evola, F. Gullo, L. Marletta, The role of shading devices to improve thermal and visual comfort in existing glazed buildings, Energy Procedia, 134 (2017) 346-355. https://doi.org/10.1016/j.egypro.2017.09.543
- G. Datta, Effect of fixed horizontal louver shading devices on thermal performance of building by TRNSYS simulation, Renew Energy, 23 (2001) 497-507. https://doi.org/10.1016/S0960-1481(00)00131-2
- R.A. Mangkuto, D.K. Dewi, A.A. Herwandani, M.D. Koerniawan, Design optimisation of internal shading device in multiple scenarios: Case study in Bandung, Indonesia, Journal of Building Engineering, 24 (2019) 100745. https://doi.org/10.1016/j.jobe.2019.100745
- A. Heidari, M. Taghipour, Z. Yarmahmoodi, The effect of fixed external shading devices on daylighting and thermal comfort in residential building, Journal of Daylighting, 8 (2021) 165-180. https://doi.org/10.15627/jd.2021.15
- A. Krstić-Furundžić, M. Vujošević, A. Petrovski, Energy and environmental performance of the office building facade scenarios, Energy, 183 (2019) 437-447. https://doi.org/10.1016/j.energy.2019.05.231
- A.K.K. Lau, E. Salleh, C.H. Lim, M.Y. Sulaiman, Potential of shading devices and glazing configurations on cooling energy savings for high-rise office buildings in hot-humid climates: The case of Malaysia, International Journal of Sustainable Built Environment, 5 (2016) 387-399. https://doi.org/10.1016/j.ijsbe.2016.04.004
- H. Sghiouri, A. Mezrhab, M. Karkri, H. Naji, Shading devices optimization to enhance thermal comfort and energy performance of a residential building in Morocco, Journal of Building Engineering, 18 (2018) 292-302. https://doi.org/10.1016/j.jobe.2018.03.018
- L. Evangelisti, C. Guattari, F. Asdrubali, R. de Lieto Vollaro, An experimental investigation of the thermal performance of a building solar shading device, Journal of Building Engineering, 28 (2020) 101089. https://doi.org/10.1016/j.jobe.2019.101089
- M.I. Serralheiro, J. de Brito, A. Silva, Methodology for service life prediction of architectural concrete facades, Constr Build Mater, 133 (2017) 261-274. https://doi.org/10.1016/j.conbuildmat.2016.12.079
- I. Marie, H. Quiasrawi, Closed-loop recycling of recycled concrete aggregates, J Clean Prod, 37 (2012) 243-248. https://doi.org/10.1016/j.jclepro.2012.07.020
- B. Zhou, Y. Uchida, Relationship between fiber orientation/distribution and post-cracking behaviour in ultra-high-performance fiber-reinforced concrete (UHPFRC), Cem Concr Compos, 83 (2017) 66-75. https://doi.org/10.1016/j.cemconcomp.2017.07.007
- J. Feng, F. Yang, S. Qian, Improving the bond between polypropylene fiber and cement matrix by nano calcium carbonate modification, Constr Build Mater, 269 (2021) 121249. https://doi.org/10.1016/j.conbuildmat.2020.121249
- C.A. Nonato Da Silva, J. Ciambella, J.A.O. Barros, T.D. dos Santos Valente, I.G. Costa, A multiscale model for optimizing the flexural capacity of FRC structural elements, Compos B Eng, 200 (2020) 108325. https://doi.org/10.1016/j.compositesb.2020.108325
- K.M. Nascimento, R.T.S. Freire, P.H. Ribeiro Borges, A.L. Christoforo, T.H. Panzera, Fiber-reinforced concrete (FRC) for civil engineering applications, in: Woodhead Publishing Series in Civil and Structural Engineering, J.B. Bai (Ed.), Woodhead Publishing, 2023, pp. 541-568. https://doi.org/10.1016/B978-0-12-820346-0.00008-3
- L. Shen, X. Yao, G. Di Luzio, M. Jiang, Y. Han, Mix optimization of hybrid steel and polypropylene fiber-reinforced concrete for anti-thermal spalling, Journal of Building Engineering, 63 (2023) 105409. https://doi.org/10.1016/j.jobe.2022.105409
- Q. Li, Z. Shi, F. Zhao, S. Yu, K. Xie, Mechanical performance evaluation of steel fiber-reinforced concrete (FRC) based on multi-mechanical indicators from split hopkinson pressure bar (SHPB) test, Journal of Building Engineering, 79 (2023) 107898. https://doi.org/10.1016/j.jobe.2023.107898
- Á. Mena-Alonso, D.C. González, J. Mínguez, M.A. Vicente, Size effect on the flexural fatigue behavior of high-strength plain and fiber-reinforced concrete, Constr Build Mater, 411 (2024) 134424. https://doi.org/10.1016/j.conbuildmat.2023.134424
- V. Farhangi, M.J. Moradi, K. Daneshvar, H. Hajiloo, Application of artificial intelligence in predicting the residual mechanical properties of fiber reinforced concrete (FRC) after high temperatures, Constr Build Mater, 411 (2024) 134609. https://doi.org/10.1016/j.conbuildmat.2023.134609
- M.F. Leone, G. Nocerino, Advanced modelling and digital manufacturing: Parametric design tools for the optimization of UHPFRC (ultra high-performance Fiber reinforced concrete) shading panels, Autom Constr, 126 (2021) 103650. https://doi.org/10.1016/j.autcon.2021.103650
- D. Whitley, S. Rana, J. Dzubera, K.E. Mathias, Evaluating evolutionary algorithms, Artif Intell, 85 (1996) 245-276. https://doi.org/10.1016/0004-3702(95)00124-7
- J.H. Holland, Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence, MIT Press, 1992. https://doi.org/10.7551/mitpress/1090.001.0001
- H. Jungjohann, W. Woodington, Ontario Celebration Zone pavilion: a large pneumatic structure, Procedia Eng, 155 (2016) 507-515. https://doi.org/10.1016/j.proeng.2016.08.054
- U. Maulik, S. Bandyopadhyay, Genetic algorithm-based clustering technique, Pattern Recognit, 33 (2000) 1455-1465. https://doi.org/10.1016/S0031-3203(99)00137-5
- S. Wright, The roles of mutation, inbreeding, crossbreeding, and selection in evolution, 1932.
- J.D. Schaffer, Some experiments in machine learning using vector evaluated genetic algorithms, Vanderbilt Univ., Nashville, TN (USA), 1985.
- D.E. Goldberg, Genetic Algorithms in Search, Optimization and Machine Learning, Addison-Wesley Longman Publishing Co., Inc., 1989.
- M. Makki, M. Showkatbakhsh, A. Tabony, M. Weinstock, Evolutionary algorithms for generating urban morphology: Variations and multiple objectives, International Journal of Architectural Computing, 17 (2019) 5-35. https://doi.org/10.1177/1478077118777236
- M. Akbari, P. Asadi, M.K. Besharati Givi, G. Khodabandehlouie, Artificial neural network and optimization, in: Advances in Friction-Stir Welding and Processing, Buckingham, England, UK, Woodhead Publishing, 2014, pp. 543-599. https://doi.org/10.1533/9780857094551.543
- F. Ascione, N. Bianco, C. De Stasio, G.M. Mauro, G.P. Vanoli, Energy Management in Hospitals, in: Comprehensive Energy Systems, vol. 5, Waltham, MA, USA, Elsevier, 2018, pp. 827-854. https://doi.org/10.1016/B978-0-12-809597-3.00541-1
- E. Zitzler, Evolutionary algorithms for multiobjective optimization: Methods and applications, vol. 63, Citeseer, 1999.
- Wallacei, Evolutionary Engine for Grasshopper3D, https://www.wallacei.com, accessed August 13, 2021.
- K. Deb, A. Pratap, S. Agarwal, T. Meyarivan, A fast and elitist multiobjective genetic algorithm: NSGA-II, IEEE Transactions on Evolutionary Computation, 6 (2002) 182-197. https://doi.org/10.1109/4235.996017
- O.A. Adekanmbi, O.O. Olugbara, J. Adeyemo, A comparative study of state-of-the-art evolutionary multi-objective algorithms for optimal crop-mix planning, International Journal of Agricultural Science and Technology, 2 (2014) 8-16. https://doi.org/10.14355/ijast.2014.0301.02
- K. Deb, M. Mohan, S. Mishra, Evaluating the ϵ-domination based multi-objective evolutionary algorithm for a quick computation of Pareto-optimal solutions, Evol Comput, 13 (2005) 501-525. https://doi.org/10.1162/106365605774666895
- S.O. Sadegh, E. Gasparri, A. Brambilla, A. Globa, Kinetic facades: An evolutionary-based performance evaluation framework, Journal of Building Engineering, 53 (2022) 104408. https://doi.org/10.1016/j.jobe.2022.104408
- EnergyPlus, https://energyplus.net/weather, accessed May 14, 2023.
- S. Samant, S. Sharples, Surface Reflectance Distributions and their Effect on Average Daylight Factor Values in Atrium Buildings, Archit Sci Rev, 47 (2004) 177-181. https://doi.org/10.1080/00038628.2004.9697041
- Y. Bian, Y. Ma, Analysis of daylight metrics of side-lit room in Canton, south China: A comparison between daylight autonomy and daylight factor, Energy Build, 138 (2017) 347-354. https://doi.org/10.1016/j.enbuild.2016.12.059
- A. Nabil, J. Mardaljevic, Useful daylight illuminance: a new paradigm for assessing daylight in buildings, Lighting Research & Technology, 37 (2005) 41-57. https://doi.org/10.1191/1365782805li128oa
- Y. Chang, Z. Bouzarkouna, D. Devegowda, Multi-objective optimization for rapid and robust optimal oilfield development under geological uncertainty, Comput Geosci, 19 (2015) 933-950. https://doi.org/10.1007/s10596-015-9507-6
- S.N. Sivanandam, S.N. Deepa, Genetic algorithms, in: Introduction to Genetic Algorithms, Springer, 2008, pp. 15-37. https://doi.org/10.1007/978-3-540-73190-0_2
Copyright © 2025 The Author(s). Published by solarlits.com.
 HOME
HOME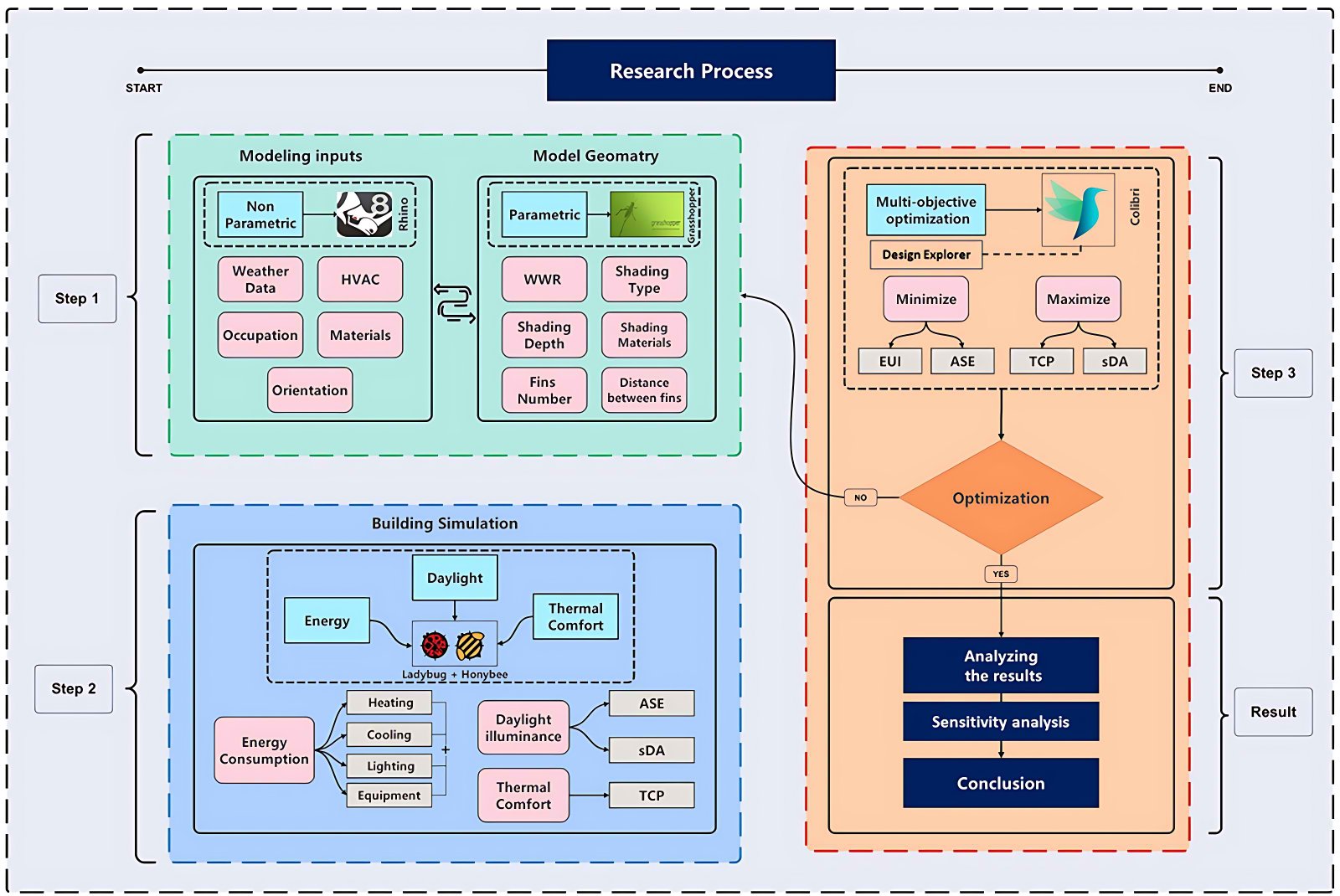 Figure 1
Figure 1 Figure 2
Figure 2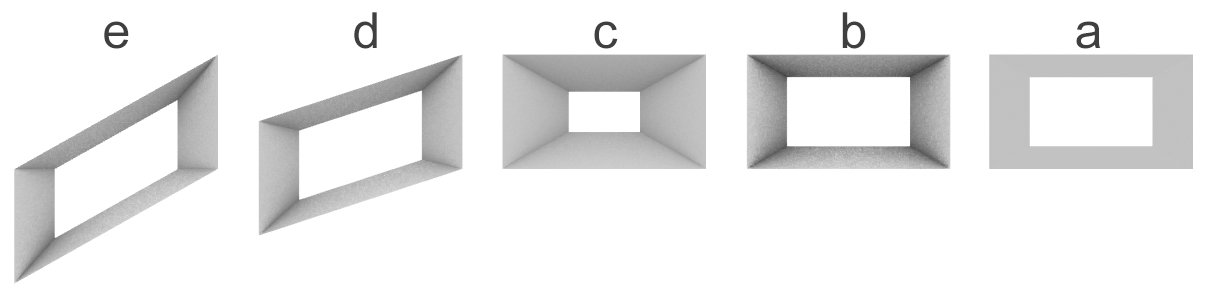 Figure 3
Figure 3 Figure 4
Figure 4 Figure 5
Figure 5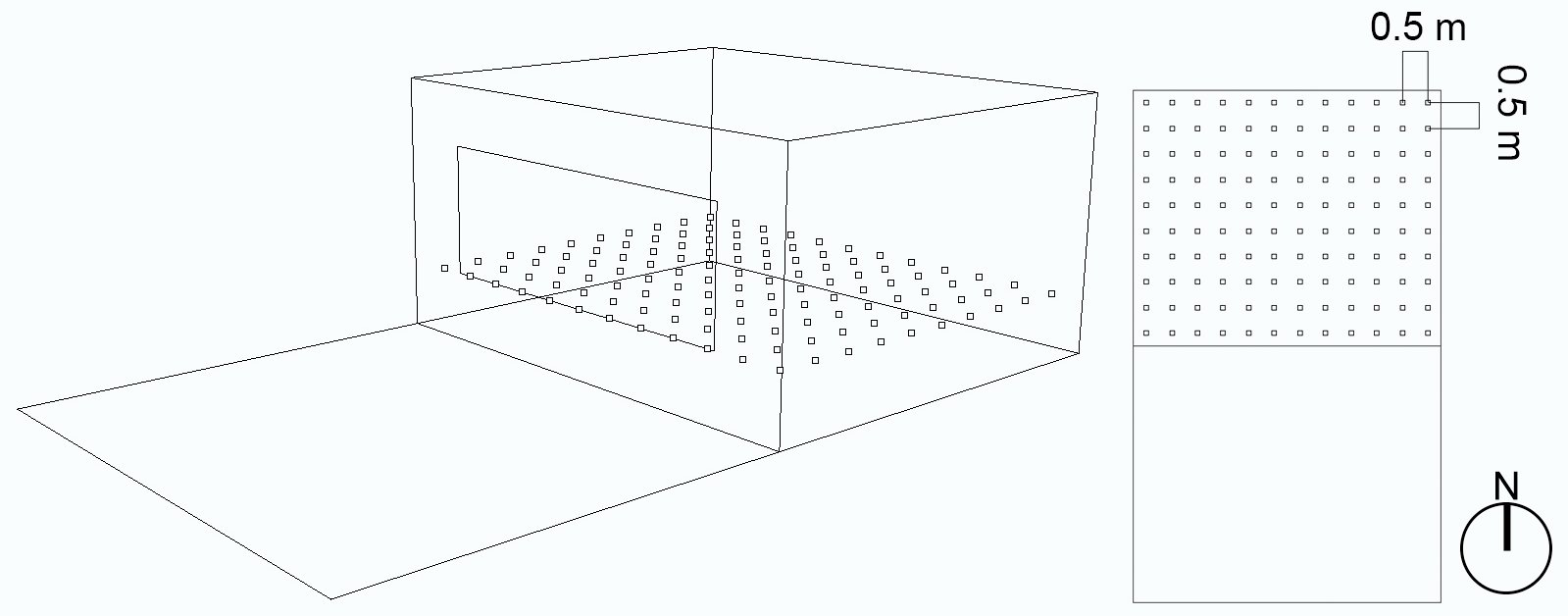 Figure 6
Figure 6 Figure 7
Figure 7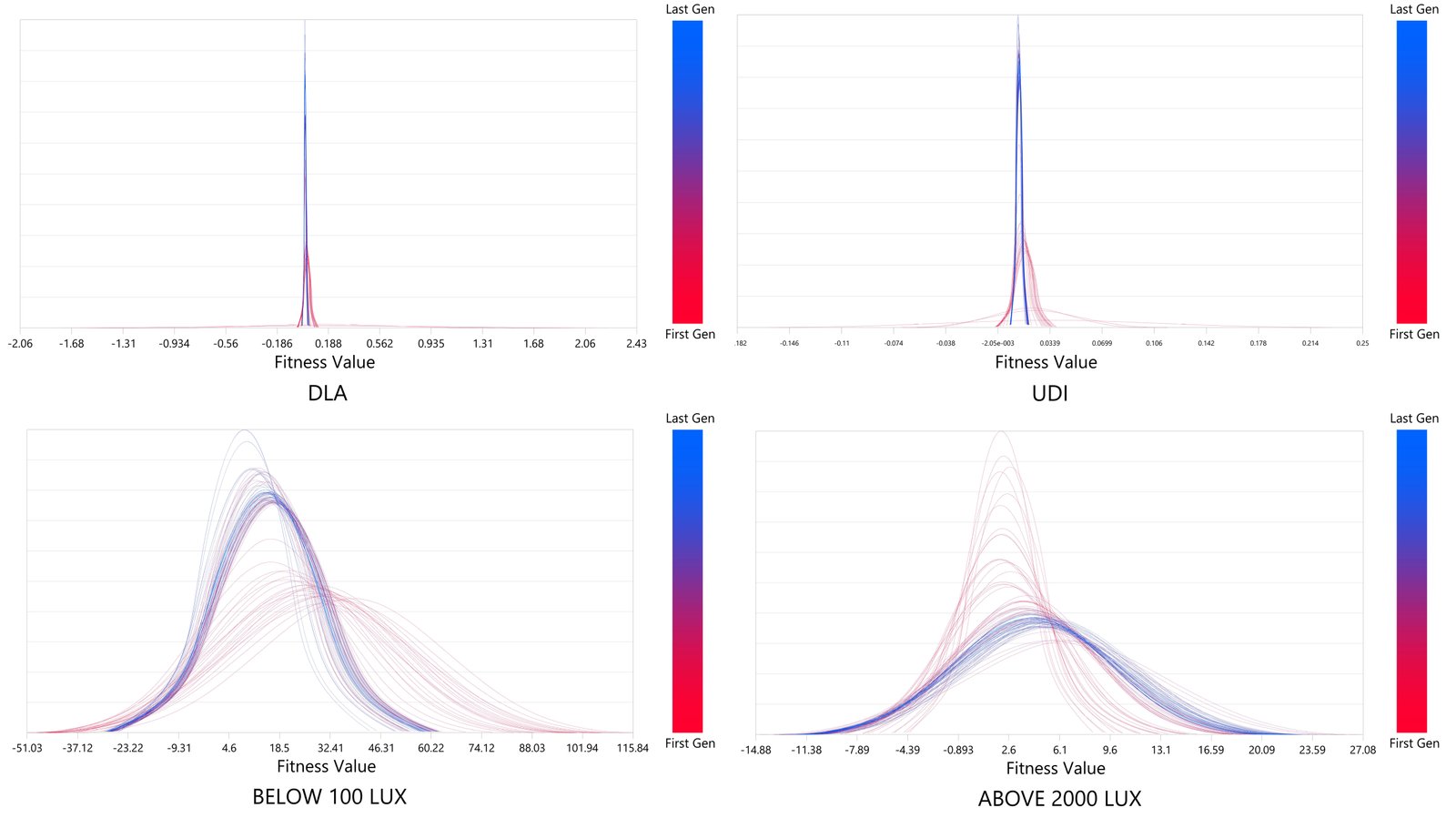 Figure 8
Figure 8 Figure 9
Figure 9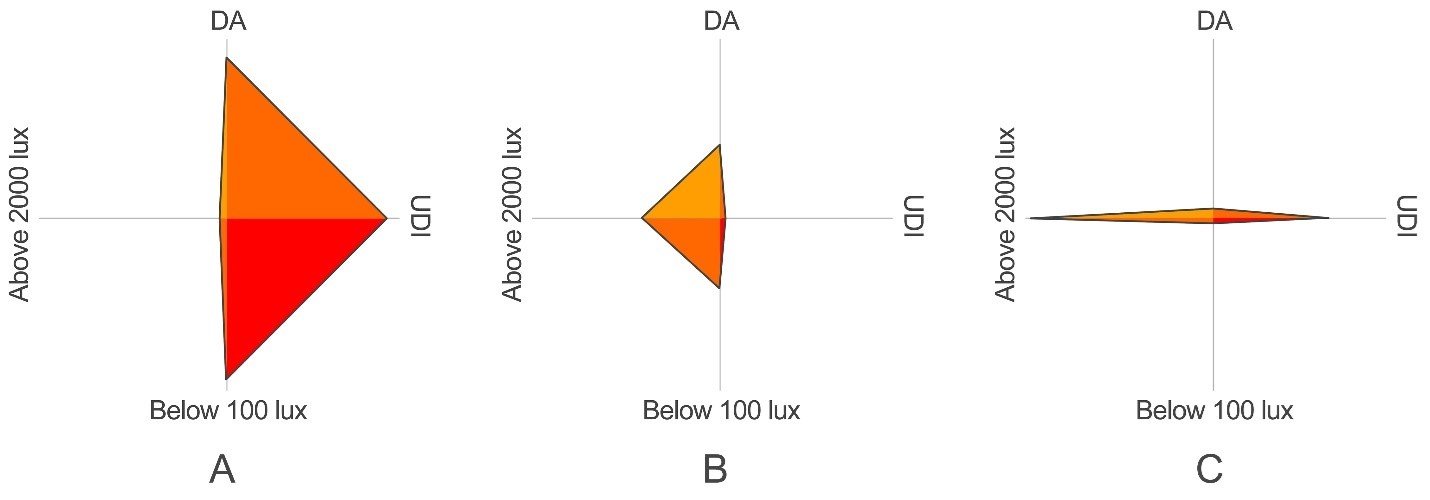 Figure 10
Figure 10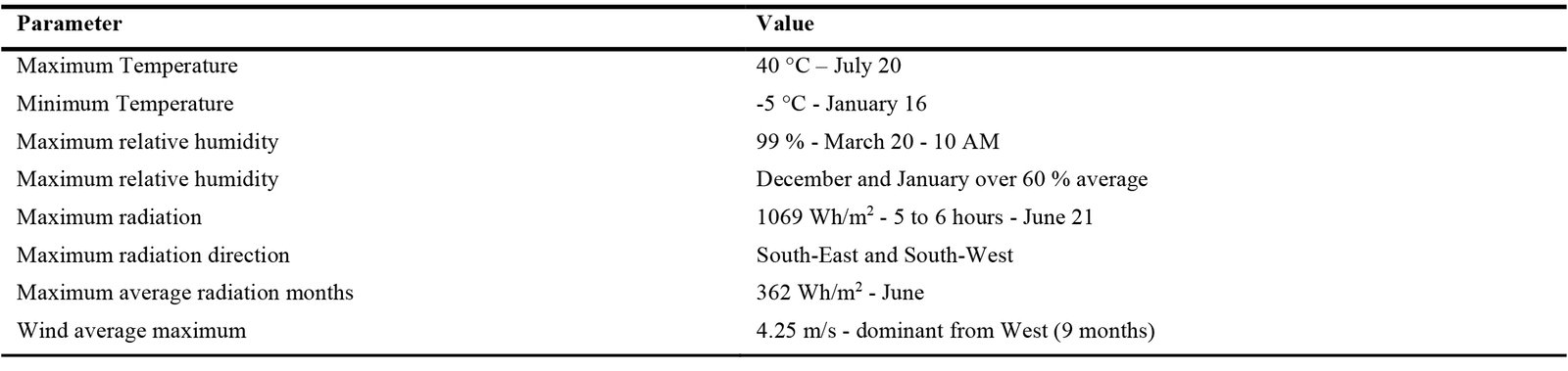 Table 1
Table 1 Table 2
Table 2 Table 3
Table 3 Table 4
Table 4 Table 5
Table 5 Table 6
Table 6 Table 7
Table 7 Table 8
Table 8 Table 9
Table 9![Pareto front scheme [52].](figures/12-111-1.jpg)



