Volume 12 Issue 2 pp. 252-264 • doi: 10.15627/jd.2025.17
Tessellation-Based Origami-Inspired Movable Façade for Daylighting and Exposure Optimization: Assessing Different Movement Approaches
Ecenur Kızılörenli,1,* Ahmet Vefa Orhon2
Author affiliations
1 Dokuz Eylül University, Graduate School of Natural and Applied Sciences, Department of Architecture, 35160 İzmir, Türkiye
2 Dokuz Eylül University, Faculty of Architecture, Department of Architecture, 35390 İzmir, Türkiye
*Corresponding author.
ecenur.kizilorenli@ogr.deu.edu.tr (E. Kızılörenli)
vefa.orhon@deu.edu.tr (A. Vefa Orhon)
History: Received 12 March 2025 | Revised 3 April 2025 | Accepted 15 April 2025 | Published online 21 June 2025
2383-8701/© 2025 The Author(s). Published by solarlits.com. This is an open access article distributed under the terms and conditions of the Creative Commons Attribution 4.0 License.
Citation: Ecenur Kızılörenli, Ahmet Vefa Orhon, Tessellation-Based Origami-Inspired Movable Façade for Daylighting and Exposure Optimization: Assessing Different Movement Approaches, Journal of Daylighting, 12:2 (2025) 252-264. doi: 10.15627/jd.2025.17
Figures and tables
Abstract
This study emphasizes the importance of daylight performance in interior spaces as a critical factor in achieving global Sustainable Development Goals, including energy efficiency, environmental sustainability, and healthy living conditions. It introduces a novel façade system inspired by tessellation-based origami principles, designed to mitigate exposure, glare and optimize daylight utilization, directly contributing to user comfort and well-being. The research employs a movable folding façade system with modular adaptability through different tessellation patterns. Performance analyses were conducted to evaluate the system's effectiveness in reducing exposure (Annual Sunlight Exposure), glare (Glare Autonomy) and improving daylight performance (Spatial Daylight Autonomy). The system’s compliance with LEED v4.1 criteria was also assessed to ensure alignment with sustainable building standards. The proposed façade system effectively reduced overexposure levels to 2.42%, enhanced sDA to 87.87% and also improved glare values by up to 50.26%. These results highlight the system’s potential to improve daylighting performance while addressing user comfort. This research presents an innovative façade system that integrates tessellation-based origami principles to optimize daylight performance. It contributes to sustainable architectural practices by demonstrating the transformative potential of movable and adaptive façade designs in achieving sustainable development goals, addressing both environmental and user comfort.
Keywords
Movable façade system, Daylight performance, Tessellation, Origami-inspired design
1. Introduction
The design of sustainable spaces has gained significant importance in response to the growing global awareness of and interest in environmental sustainability [1]. This shift has been further catalyzed by the 2030 Agenda for Sustainable Development, which encompasses the Sustainable Development Goals (SDGs) adopted in 2015 by all 193 United Nations Member States to address environmental, social, and economic challenges [2]. These goals collectively aim to ensure the peace and well-being of both the planet and its inhabitants. Among the 17 SDGs, three—SDG 3 (Good Health and Well-being), SDG 7 (Affordable and Clean Energy), and SDG 11 (Sustainable Cities and Communities)—are directly aligned with the role of illumination in sustainable development. In this context, daylight integration in architectural practice transcends its traditional role, becoming a central element of sustainable design. Architects and designers are increasingly adopting strategies that not only optimize natural light utilization but also contribute to achieving broader ecological and sustainability objectives.
In these aspects, evolving technology as a member of the modern world plays a significant role, enabling different parts of buildings to be updated to impact energy consumption or enhance user comfort. The building envelope, being one of the primary components continuously exposed to climatic conditions, is expected to possess adaptability to accommodate changes [3]. Initially, the fundamental functions of the building envelope include controlling the climate's impact between indoor and outdoor spaces, mitigating noise to ensure a healthy environment for occupants, and as will be discussed in this study, regulating daylight to ensure visual comfort [4,5]. With the advancement of digital modeling tools and parametric modeling, contemporary building facades offer a broader range of design possibilities for complex geometric shapes and forms. In this regard, the flexibility and optimizability offered by parametric modeling play a crucial role in the design of dynamic structural elements such as movable facades in modern architecture [6]. Movable facades are structural elements with features that enable buildings to respond to external conditions while simultaneously integrating architectural functionality. Utilizing these tools enables efficient capture of sunlight angles into the building's interior, facilitating efficient space utilization and creating a visually comfortable environment for users. While striving to increase the amount of daylight entering the space, designers should aim to create balanced designs that maximize the benefits of daylight while minimizing the risk of discomfort [7].
Among these, mentioned moveable systems, studies of parametric design and building facades were present in the literature. It was seen from Table 1 that this field of study gained higher numbers within the last five years. Listed and classified according to the module forms, these works represent an outstanding advance within the field.
As seen in the table, proposals have been developed that employ different modules and geometries in systems with various functions, and consequently, different facade designs have been chosen. In these systems, which have diverse objectives, daylight and glare analyses have been conducted to achieve optimal results. It is evident from these proposals that there is no study in the literature that examines a tessellation-based folding movement system, where the applied method can be used in multiple layouts and evaluates the interior daylight and glare performance of the targeted system. In addition to this gap in the literature, when it comes to facades with proposed and applied movable shading systems, the design alternatives, as can be understood from the examples, have unlimited potential. This contributes to solving problems and deficiencies arising from implementations on different facades and locations. To fill these identified gaps, this study proposes three different façade systems consisting of modules exhibiting origami-based folding movements based on three different geometries. It aims to evaluate the visual comfort of the users and to investigate the performance of reducing exposure and glare levels while improving daylight performance in interior spaces. While aiming for multiple efficient configurations to support the concept of movement, this study aims to keep the glass transmittance and material properties within the proposed system constant and out of scope, thus providing alternative uses. The results were obtained by simulating the proposals and each movement approach, and the results were compared with the base scenario and discussed.
2. Theoretical background of the study
2.1. Tessellation, types and architecture
The term "tessellation" derives from the Latin word "tessella" and the Greek word "tessera," which refer to small square stones [23]. This technique, used in architecture and art since ancient times, involves covering a surface with geometric shapes without gaps or overlaps, thus creating patterns through the repetition of certain shapes [24]. Regular tessellation (RT) involves the repetition of the same type of regular polygon, such as triangles, squares, and hexagons (Fig. 1). Semi-regular tessellation (SRT) includes two or more types of regular polygons arranged consistently at each vertex, with only eight possible configurations (Fig. 1). Demi-regular tessellation (DRT), a combination of regular and semi-regular patterns, offers 20 different examples (Fig. 1) [25,26].
2.2. Origami in architecture
The term "origami" derives from the Japanese words "oru," meaning to fold, and "kami," meaning paper [27]. Although there is no definitive information about the origins of origami, it is believed to have been discovered in China over 1200 years ago and later developed in Japan by Buddhist monks. It was then introduced to Europe, particularly to Spain, via the Silk Road [28], subsequently spreading worldwide and finding applications in various fields. One such field is design, where it has been utilized for centuries for various purposes. Origami allows for the creation of patterns in two dimensions, the addition of three-dimensional qualities through folding, and the alteration of surface qualities or enhancement of structural strength through folds. Consequently, it can be employed in architectural systems for aesthetic, spatial definition, and load-bearing purposes [29].
3. Material and method of the research
The facade created through this complex process and decision-making must be simple, flexible, and operate smoothly. This study consists of modeling, simulation, and optimization conducted after a multi-stage design process. When examining these stages in order, the potential use of tessellation methods and origami-inspired modules, and the idea of applying a system formed by combining these two approaches as a movable second layer, is introduced. Among the process in developing the system proposal are the ease of iterating the shapes and modular system of the produced modules, the ability to produce different patterns using the modules, the modules' movement without obstructing each other, avoiding gaps and overlaps when covering the facade, and the primary goal of controlling daylight and preventing unwanted heat gain [21]. It was decided to use a simple mechanism that would allow the panels to be folded without interfering with each other. Although material selection and comparison were not included in the study, to solely analyze the performance of the proposed facade patterns, the impact of material changes on daylight analysis results was avoided.
3.1. Research area and simulated model
The office structure chosen as the workspace is in Izmir province, Turkey, between approximately 37.9° N to 39.2° N in latitude and 26.7° E to 28.3° E in longitude. Although climate types across the country are classified into multiple categories, the selected location falls under the Csa category according to the Köppen-Geiger classification, indicating a warm-summer Mediterranean climate with mild winters and hot, dry summers [30]. The office structure has been parametrically modeled to represent a typical volume. The modeled space measures 6 meters deep, 8 meters wide, and 3 meters high. The room was designed with an opening only on the south facade, constituting approximately 76.6% of the facade area. Material selections within the space were chosen according to LEEDv4.1 (Fig. 2) [31]. Reflectance values of 80% for the ceiling, 20% for the floor, and 50% for the walls were selected. Azuria glass with 67.4% transmittance, which was also used by Özdemir and Çakmak in their studies [14], was used as single-glazed glass. While these reflection values were defined as material values with Grasshopper and Ladybug tools, the specularity and roughness values of the relevant elements were kept at 0.1 in line with the studies in the literature [32,33]. Although the proposed façade elements were selected from the Radience Material Library in Dirty White color and properties (Reflectance: 34.1%, Specularity: 0, Roughness: 0.33), the system was designed without being tied to a specific material. Instead of the selected material, a series of materials with varying optical properties can be varied to have similar reflectance values [34]. The important point was determined to be constant values in all models and all configurations. All of these selections were integrated using the Honeybee and Ladybug tool with Grasshopper.
3.2. Origami-inspired modular movable facade design and tested modules
In recent years, origami-based designs have attracted widespread attention in the field of adaptable façades, as can be seen in the literature [10,13,16,18,19,20,22]. However, relatively few solutions have been implemented in real-world scenarios [34]. This contrast may be due to the often overly complex geometries considered in the early design stages, the difficulties in translating mechanisms into real structures, and the lack of attention to practical issues such as maintenance, operation, and running costs. Within the scope of this paper, a design process consisting of several stages was planned, taking these elements into account. Initially, small modules were created based on basic folding principles. Subsequently, the module was refined by evaluating numerous criteria, such as ease of folding, ensuring that panels and modules do not obstruct or interfere with each other during folding, and minimizing protrusion from the façade when folded.
The inception of the design process began with a hands-on exploration phase characterized by manual folding experiments. The primary objective of these experiments was to understand the modularity of origami patterns and evaluate their potential to embody the desired characteristics within the envisioned façade system. These experiments were initially conducted using A4 paper, scaled to different sizes. Basic and simple folds were produced at small scales to prioritize quick and efficient production, facilitating a smoother testing process (Table 2). The following compiled table presents the modules that were selected by the authors as most suitable for the design objective. This evaluation framework serves as a fundamental step in defining the modules.
The modules obtained were evaluated, and selections were made based on the established criteria. The "h" module was chosen due to its ability to open and close without affecting other modules, its independent movement from the other panels, the amount of displacement from the facade during its movement, and its ability to maintain the same length throughout its motion. The goal was to produce facade modules in three geometries from this folded module: triangle, square, and hexagon. The fundamental principle behind the creation of each was the same. Triangles were created with thick dark red lines framing them, the folding movement was defined, and then it was derived to reach the target geometry (Fig. 3). The study primarily focused on the created triangular modules. When producing this triangular module, a fold was proposed starting from the short side (side 'a') of the right triangle. This decision was made because the movement of the elements derived along the arc defined as the folding path does not interfere with each other. Similarly, another decision made was that the height 'd' within the mountains and valleys should remain the same when the folding movement is completed. This is achieved not by dividing the short side near the folding axis into equal parts, but by dividing the corresponding alpha angle into equal parts. Although this study divides it into four parts, it can be divided by a different factor. Thus, when the module is fully closed, the height of each element remains equal.
In this context, each module's side length 'a' is determined to be 0.5 meters to maintain consistent dimensions between modules, ensuring a consistent comparison of methods and models. This results in a total module side length of 1 meter. This approach aims to ensure compatibility with the proposed base case model, while keeping the simulation and optimization time as short as possible and the performance evaluation reasonably effective. Therefore, when dimension 'a' is set to 0.5 meters, dimension 'b' follows the rules of 30-60-90 and 45-45-90 triangles. The critical point here is that the arc segment identified as the folding path is determined based on the movement of side a. Similarly, during modeling with Grasshopper, it was ensured that the lengths of all edges designated as mountain and valley remained constant. To form the triangular module, the red-framed triangle (Fig. 3) needs to be derived six times for the triangle, eight times for the square, and twelve times for the hexagon. This approach prevents any element from deforming during movements (Fig. 4). This allows for the possibility of choosing a rigid or flexible material in subsequent studies if material selection becomes necessary.
After completing the modules, three types of tessellation patterns were identified from different categories, and three different configurations of façade models were derived. One example was selected from each category: RT, SRT and DRT (Fig. 5). For the analysis of these examples, the same materials were assigned to each, and the models were constructed.
Simultaneously, as illustrated in the image, this approach extends its applicability to squares and triangles. This not only demonstrates the versatility of the method but also supports the usability and derivability of semi-regular and demi-regular patterns—categories that, as previously asserted, were not documented in existing literature. The adaptability of the technique to squares and triangles showcases its potential to generate a broader spectrum of patterns beyond conventional folds. This approach supports previous assumptions about pattern limitations for the exploration of novel designs and configurations (Fig. 5). Moreover, since the system operates modularly, modules can be removed as needed, demonstrating the system's capability to create openings as required. This feature adds an extra layer of functionality, allowing for customizable designs that incorporate apertures or voids within the overall structure. Such adaptability enhances the practicality and creative possibilities of the folding method, suggesting its potential in a variety of applications where tailored patterns and configurations are desired.
3.3. Definition of the parameters and simulation workflow
The shape resulting from the movement of the panels and the area it covers on the façade affects the amount of daylight reaching the interior. The dynamic daylight metrics used, which focus on the movements of these variables, are Spatial Daylight Autonomy (sDA) and Annual Sunlight Exposure (ASE), as determined by LEED and Glare Autonomy (GA) used in recent literature [35-39].
Spatial Daylight Autonomy (sDA) represents the percentage of time during specific hours of the day, typically business hours, throughout the year that a certain level of natural daylight penetrates the interior of a building. For a space to meet the requirements, it must receive at least 300 lux for 50% of the annual occupied hours. According to LEED v4.1, 1 point is earned for 40% value, 2 points for 55% value, and 3 points for 75% value. Annual Sunlight Exposure (ASE) measures the amount of time throughout the year that a specific interior space within a building is exposed to direct sunlight exceeding a certain threshold. This metric helps evaluate the potential excessive impact of sunlight on indoor environments, assessing the risk of overheating. Low ASE values indicate minimal exposure to direct sunlight, contributing to enhanced indoor comfort and reduced cooling loads. The criterion typically requires that no more than 10% of the floor area receive more than 250 hours of direct sunlight (1000 lux or more) annually [40]. In the glare analysis included in the study to comprehensively evaluate user comfort, the Glare Autonomy (GA) metric was used, which measures the ratio of hours with a DGP (Daylight Glare Probability) value below 0.35. DGP is an index that rates the glare intensity at a point between 0 (no glare) and 1 (intolerable glare), and the acceptable upper limit in GA calculations was determined as DGP ≤0.35 (imperceptible glare) [39]. All analyses, together with the ASE (Annual Sunlight Exposure) and sDA (Spatial Daylight Autonomy) metrics, were conducted considering the active usage hours of the space, between 09:00 and 17:00. Movable shading systems aimed to balance both daylight performance and maximize the visual comfort of users by analyzing these three metrics in an integrated manner, while remaining within the acceptable DGP limits.
Various facade models have been generated based on three selected patterns in order to evaluate the mentioned metrics (Fig. 6). For the evaluation of these models, three variations based on different movement approaches have been produced for each model. These approaches are as follows: in the first approach, the modules in each model (regular, semi-regular, and demi-regular) exhibit total movement (TM), meaning that when one module moves at a certain angle, all modules move at the same angle. In the second approach, horizontal elements are grouped, and the elements within each group move (GM) at the same angle. Therefore, while each group moves at the same angle, different movements can be observed between the groups, allowing for the formation of different configurations. In the final approach, each module on the facade can perform their individual movement (IM). This theory increases the usage alternatives according to the interior needs but complicates the performance analysis of the facade. Thus, since three approaches will be tested for each pattern, a total of nine different analysis processes have been conducted simultaneously.
As illustrated in Fig. 7, the study consists of five steps. Due to the changes in parameters caused by the movement approach and the large number of variables in each model, the optimization of the evaluation process was carried out using another plugin, Octopus. The process progressed by revisiting previous steps and making corrections. Finally, the resulting data, after being deemed efficient, was transformed into a table using the TT Toolbox plugin and Excel (Fig. 8). The configurations that led to the most efficient results were visualized, and the corresponding sDA, ASE and GA values were presented for analysis.
3.3.1. Evaluated models
As stated in the section 3.2, the selected patterns were modeled using Grasshopper. To facilitate tracking the movement of the module angles in the evaluated models, Fig. 9 was created. For each initial model of the patterns, the number of parameters included in the simulation is one (Fig. 8). Additionally, for the second model of the RT, in which modules move as a group, the number of parameters included in the optimization is seven, while in the case where each module moves independently, the number of parameters increases to forty-six. For the SRT, the number of parameters is five in the second approach and thirty-two in the third approach. In the case of the DRT, the second approach involves six parameters, whereas the third approach includes twenty-three parameters. In both the second and third approaches, panels and groups were sequentially numbered in the visualization to facilitate the easy tracking of daylight performance results within the interior space based on the movements of the panels.
Figure 9
Fig. 9. Panel configurations and parameters for optimization process, left: TM, middle: GM, right: IM.
4. Parametric analysis and findings
The analysis and evaluations were initially conducted for the base case scenario to allow comparison with the current scenario. As a result, the sDA value was found to be 100%, while the ASE value was 72.73% and GA value was 60.39% (Fig. 10). It is evident that although the sDA value is significantly high, the ASE value, which should ideally be below 10%, is far above this threshold, potentially causing discomfort for occupants. Therefore, the necessity for implementing the proposed system is clearly demonstrated.
The evaluation process of the system began with the collective movement of each pattern type. These evaluations were completed by limiting the movement of the panels to increments of 5 degrees for time efficiency. As a result, the panels could be positioned in 18 different configurations, ranging from 0 to 90 degrees in 5-degree increments. Subsequently, the daylight performance of the interior space was analyzed for each of the 18 configurations of the panels designed with different types of tessellations.
Figure 10
Fig. 10. Daylight performance analysis of the base case (left: sDA, middle: ASE, right: GA).
As shown in Table 3, the most efficient results for all three models were obtained when the panels were positioned at a 30-degree angle. The results indicated that for the first model (RT), the sDA value was 44.84%, the ASE value was 8.48% and the GA value was 91.99%; for the second model (SRT), the sDA value was 47.34%, the ASE value was 9.76% and the GA value was 94.28%; and for the third model (DRT), the sDA value was 40.93%, the ASE value was 9.92% and the GA value was 91.70%. As discussed in Section 3.3, while the sDA value for all three models exceeded the 40% threshold and GA value kept over 90% and the ASE value remained below the 10% threshold (Fig. 11).
Figure 11
Fig. 11. Daylight performance results of the first approach (left: RT, middle: SRT, right: DRT).
In the second approach, simulations were repeated using grouped movements as described in Fig. 9. During the optimization process, each model included different numbers of parameters, with two objectives defined: sDA and ASE. Additionally, another objective was defined in this process due to the specific values that needed to be met for sDA and ASE. To achieve this, an "Expression" component was used to write conditions for these two values, ensuring that their sum was also defined as an objective. These expressions are defined as “if(x > 10, x - 10, 0)” for ASE and “if(x < 55, 55 - x, 0)” for sDA. This aimed to reduce results that did not meet these conditions, thereby accelerating the process of obtaining more efficient outcomes. For the optimization, the population size was set to 150, and the maximum number of generations was defined as 15. The average evaluation time was approximately 65.13 seconds. At the end of this process, to identify the most efficient results, solutions with an sDA value below 40 and an ASE value above 10 were deliberately excluded from the table. For the remaining data, the values were evaluated using the fitness function, a mathematical function designed to assess the quality of a solution. In this study, this function calculates the difference between SDA and ASE and ranks the configurations of the design that give efficient results by sorting this difference from largest to smallest. Afterwards, GA analyses were performed with these configurations. The top five values obtained for each model are presented in Table 4. The panel locations and visualized simulation results are shown in Fig. 12.
In evaluating the first model (RT), the most efficient result showed the sDA value of 72.73%, the ASE value of 7.27% and the GA value of 88.36%. The folding angles of the seven grouped panels, from Group 1 to Group 7, were 85°, 5°, 20°, 35°, 15°, 15°, and 45°, respectively. For the second model (SRT), the most efficient result yielded the sDA value of 79.39%, the ASE value of 8.48% and the GA value of 90.74%. The panel locations, from 1 to 5, had folding angles of 75°, 0°, 0°, 0°, and 55°, respectively. For the final model (DRT), the most efficient result achieved the sDA value of 68.48%, the ASE value of 2.42%and the GA value of 89.93%. The panels, from 1 to 6, had folding angles of 65°, 30°, 10°, 30°, 10°, and 70°, respectively.
Figure 12
Fig. 12. Daylight performance results of the second approach (left: RT, middle: SRT, right: DRT).
As the final step of the simulation and optimization process, the same steps as in the previous phase were followed. However, since the number of parameters in the final approach was determined to be 46, 32, and 23 for the models, respectively (Fig. 9), the angles for each panel were not tabulated. The panel location configurations and the visualized simulation results for each model are presented in Figs. 13 and 14. The most efficient results for the first model were obtained with the sDA value of 63.3%, the ASE value of 7.88% and the GA value of 90.42%. For the second model, the sDA value was 83.63%, the ASE value was 9.7% and the GA value was 89.49%. For the final model, the sDA value was 87.87%, the ASE value was 9.7% and the GA value was 84.53%.
Figure 13
Fig. 13. Panel angles of the selected configurations of the third approach (left: RT, middle: SRT, right: DRT).
Figure 14
Fig. 14. Daylight Performance Results of the Third Approach (left: RT, middle: SRT, right: DRT).
5. Discussion and conclusion
Balanced daylight usage in interior spaces not only increases energy efficiency but is also an important element that directly affects user comfort. Achieving this balance requires a complex optimization process in building designs. Improper management of daylight can lead to visual disturbances such as glare and contrast problems, both increasing energy consumption and negatively affecting the user experience in interior spaces. Therefore, innovative technologies such as movable facade systems can optimize daylight performance in interior spaces. In this study, the daylight performance of an office building facade with and without the proposed movable facade system was compared using ASE (Annual Sunlight Exposure), sDA (Spatial Daylight Autonomy) and GA (Glare Autonomy) metrics to analyze compliance with LEEDv4.1 standards. In the base case scenario, the fact that ASE values exceeded acceptable limits and sDA and GA were below standards revealed that the system was inadequate in terms of both daylight performance and visual comfort. With the movable façade, a noticeable improvement in daylight management is observed: ASE value is improved by 96.67%, excessive exposure is controlled, sDA value is increased by 115.22% to provide sufficient daylight access to spaces, and glare duration is reduced to acceptable levels with a performance of 82% in GA metric.
When the proposed systems that provide these efficient results are compared with the façade system proposals in the literature, it can be seen as a contribution to the literature in terms of providing more system proposals based on tessellation. The folding-movement modular approach increases the flexibility and adaptability of the system, allowing the creation of new configurations suitable for different patterns and geometries. In this way, it is possible to create the desired gaps on the façade and provide more efficient daylight management. Another important advantage of the proposed movable system is that it can be flexibly adapted to different geographical conditions and user needs. This shows that the system can maintain its effectiveness in different climate and usage scenarios around the world. However, the mechanical details of the movable façade system, material selection of the modules, glass transmittance are important factors affecting the long-term performance of the system. Therefore, focusing future research on these test parameters will make the system more efficient. In addition, practical aspects such as cost-effectiveness, installation and maintenance of the system should also be considered. In conclusion, this study demonstrates the potential of the proposed movable façade systems to provide efficient daylight use in interior spaces. More comprehensive studies in the future can further improve the design of such movable façade systems and increase energy efficiency and user comfort more effectively.
Contributions
E. Kızılörenli: Conceptualization, Methodology, Writing-original draft, Visualization, Investigation, Validation, Writing- review & editing. A. V. Orhon: Supervision, Conceptualization, Methodology, Software, Data curation, Investigation, Writing- review & editing.
Declaration of competing interest
The authors declare no conflict of interest.
References
- Y. Güney Yüksel and F. C. Seçer Kariptaş, Konut iç mekanına sürdürülebilir yaklaşımlar, Yakın Mimarlık Dergisi, 2 (2019) 27-39.
- United Nations, Transforming our world: The 2030 Agenda for Sustainable Development, United Nations, 2015. [Online] Available: https://www.un.org/ga/search/view_doc.asp?symbol=A/RES/70/1&Lang=E (accessed 21 October 2024).
- Badarnah, L., Form follows environment: Biomimetic approaches to building envelope design for environmental adaptation, Buildings, 7(2) (2017) 40. https://doi.org/10.3390/buildings7020040
- K. Amasyali and N. M. El-Gohary, A review of data-driven building energy consumption prediction studies, Renewable and Sustainable Energy Reviews, 81 (2018) 1192-1205. https://doi.org/10.1016/j.rser.2017.04.095
- N. Nasrollahi and E. Shokri, Daylight illuminance in urban environments for visual comfort and energy performance, Renewable and Sustainable Energy Reviews, 66 (2016) 861-874. https://doi.org/10.1016/j.rser.2016.08.052
- Y. C. Chan and A. Tzempelikos, A simulation and experimental study of the impact of passive and active façade systems on the energy performance of building perimeter zones, ASHRAE Transactions, 118(2) (2012).
- S. M. Kaya and Y. Afacan, Effects of daylight design features on visitors' satisfaction of museums, Indoor and Built Environment, 27(10) (2018) 1341-1356. https://doi.org/10.1177/1420326X17704028
- S. M. Hosseini, M. Mohammadi, and O. Guerra-Santin, Interactive kinetic façade: Improving visual comfort based on dynamic daylight and occupant's positions by 2D and 3D shape changes, Building and Environment, 165 (2019) 106396. https://doi.org/10.1016/j.buildenv.2019.106396
- S. M. Hosseini, M. Mohammadi, T. Schröder, and O. Guerra-Santin, Integrating interactive kinetic façade design with colored glass to improve daylight performance based on occupants' position, Journal of Building Engineering, 31 (2020) 101404. https://doi.org/10.1016/j.jobe.2020.101404
- L. Le-Thanh, T. Le-Duc, H. Ngo-Minh, Q. H. Nguyen, and H. Nguyen-Xuan, Optimal design of an Origami-inspired kinetic façade by balancing composite motion optimization for improving daylight performance and energy efficiency, Energy, 219 (2021) 119557. https://doi.org/10.1016/j.energy.2020.119557
- N. Heidari Matin and A. Eydgahi, A data-driven optimized daylight pattern for responsive façades design, Intelligent Buildings International, 14(3) (2022) 363-374. https://doi.org/10.1080/17508975.2021.1872478
- B. Dabaj, M. Rahbar, and B. V. Fakhr, Impact of different shading devices on daylight performance and visual comfort of a four opening sides' reading room in Rasht, Journal of Daylighting, 9(1) (2022) 97-116. https://doi.org/10.15627/jd.2022.7
- S. O. Sadegh, E. Gasparri, A. Brambilla, and A. Globa, Kinetic facades: An evolutionary-based performance evaluation framework, Journal of Building Engineering, 53 (2022) 104408. https://doi.org/10.1016/j.jobe.2022.104408
- H. Özdemir and B. Y. Çakmak, Evaluation of daylight and glare quality of office spaces with flat and dynamic shading system facades in hot arid climate, Journal of Daylighting, 9(2) (2022) 197-208. https://doi.org/10.15627/jd.2022.15
- S. Besbas, F. Nocera, N. Zemmouri, M. A. Khadraoui, and A. Besbas, Parametric-based multi-objective optimization workflow: Daylight and energy performance study of hospital building in Algeria, Sustainability, 14(19) (2022) 12652. https://doi.org/10.3390/su141912652
- E. Kızılörenli and A. Tokuç, Parametric optimization of a responsive façade system for daylight performance, Journal of Architectural Sciences and Applications, 7(1) (2022) 72-81. https://doi.org/10.30785/mbud.1038768
- S. S. Golzan, M. Pouyanmehr, and H. Sadeghi Naeini, Recommended angle of a modular dynamic façade in hot-arid climate: daylighting and energy simulation, Smart and Sustainable Built Environment, 12(1) (2023) 27-37. https://doi.org/10.1108/SASBE-04-2021-0075
- G. Dev and A. Saifudeen, Dynamic facade control systems for optimal daylighting, a case of Kerala, Sustainability Analytics and Modeling, 3 (2023) 100018. https://doi.org/10.1016/j.samod.2023.100018
- M. Meloni, Q. Zhang, J. Cai, and D. S. H. Lee, Origami-based adaptive facade for reducing reflected solar radiation in outdoor urban environments, Sustainable Cities and Society, 97 (2023) 104740. https://doi.org/10.1016/j.scs.2023.104740
- H. Toodekharman, M. Abravesh, and S. Heidari, Visual comfort assessment of hospital patient rooms with climate responsive facades, Journal of Daylighting, 10(1) (2023) 17-30. https://doi.org/10.15627/jd.2023.2
- E. Kızılörenli and F. Maden, Modular responsive facade proposals based on semi-regular and demi-regular tessellation: Daylighting and visual comfort, Frontiers of Architectural Research, 12(4) (2023) 601-612. https://doi.org/10.1016/j.foar.2023.02.005
- F. Wagiri, S. G. Shih, K. Harsono, and D. C. Wijaya, Multi-objective optimization of kinetic facade aperture ratios for daylight and solar radiation control, Journal of Building Physics, 47(4) (2024) 355-385. https://doi.org/10.1177/17442591231219793
- D. Seymour and J. Britton, Introduction to Tessellations, Dale Seymour Publications, Palo Alto, CA, 1989.
- E. Gjerde, Origami Tessellations: Awe-Inspiring Geometric Designs, CRC Press, 2008. https://doi.org/10.1201/b10664
- L. C. Kinsey and T. E. Moore, Symmetry, Shape and Space: An Introduction to Mathematics Through Geometry, Springer Science & Business Media, 2006.
- B. Grünbaum and G. C. Shephard, Tilings by Regular Polygons, Mathematics Magazine, 50(5) (1977) 227-247. https://doi.org/10.1080/0025570X.1977.11976655
- R. Beech, The Practical Illustrated Encyclopedia of Origami: The Complete Guide to the Art of Paperfolding, Lorenz Book, 2009.
- B. Tuğrul and M. Kavici, Kağıt Katlama Sanatı Origami ve Öğrenme, Pamukkale Üniversitesi Eğitim Fakültesi Dergisi, 11(11) (2002) 1-17.
- A. D. Yücebaş and C. Tüker, Katlama Yoluyla Örüntü Üretimi, in: Proceedings of X. Mimarlıkta Sayısal Tasarım Ulusal Sempozyumu, İstanbul Bilgi Üniversitesi Mimarlık Fakültesi, Turkey, 27-28 June 2016.
- Ministry of Forestry and Water Affairs, General Directorate of Meteorology, Köppen İklim Sınıflandırmasına Göre Türkiye İklimi, Ministry of Forestry and Water Affairs, 2023. [Online] Available: https://www.mgm.gov.tr/files/iklim/iklim_siniflandirmalari/koppen.pdf (accessed 3 April 2025).
- U.S. Green Building Council, LEED v4.1 Daylight and Quality Views Calculator, U.S. Green Building Council, 2021. [Online] Available: https://www.usgbc.org/resources/leed-v41-daylight-and-quality-views-calculator (accessed 28 December 2024).
- A. Goharian, M. Mahdavinejad, M. Bemanian, and K. Daneshjoo, Designerly optimization of devices (as reflectors) to improve daylight and scrutiny of the light-well's configuration, Building Simulation, 15 (2021) 1-24. https://doi.org/10.1007/s12273-021-0839-y
- R. Abdollahi Rizi, H. Sangin, K. Haghighatnejad Chobari, A. Eltaweel, and R. Phipps, Optimising daylight and ventilation performance: a building envelope design methodology, Buildings, 13 (2023) 2840. https://doi.org/10.3390/buildings13112840
- J. A. Jakubiec, Data-driven selection of typical opaque material reflectances for lighting simulation, LEUKOS, 19 (2023) 176-189. https://doi.org/10.1080/15502724.2022.2100788
- M. Sabouri Kenarsari, A. Baghaei Daemei, and M. Delshad Siyahkali, Parametric design on daylighting and visual comfort of climatic responsive skins through Iranian traditional girih tile, Journal of Energy Management and Technology, 5 (2021) 29-35.
- A. Galatioto and M. Beccali, Aspects and issues of daylighting assessment: A review study, Renewable and Sustainable Energy Reviews, 66 (2016) 852-860. https://doi.org/10.1016/j.rser.2016.08.018
- A. Tabadkani, S. Banihashemi, and M. R. Hosseini, Daylighting and visual comfort of oriental sun responsive skins: A parametric analysis, Building Simulation, 11 (2018) 663-676. https://doi.org/10.1007/s12273-018-0433-0
- A. Ibrahim, M. Alsukkar, Y. Dong, and P. Hu, Improvements in energy savings and daylighting using trapezoid profile louver shading devices, Energy and Buildings, 321 (2024) 114649. https://doi.org/10.1016/j.enbuild.2024.114649
- N. L. Jones, Fast climate-based glare analysis and spatial mapping, in: Proceedings of Building Simulation 2019: 16th Conference of IBPSA, Rome, Italy, 2-4 September 2019, pp. 982-989.
- Daylight Metrics Committee, Approved Method: IES Spatial Daylight Autonomy (sDA) and Annual Sunlight Exposure (ASE), Illuminating Engineering Society, 2013. [Online] Available: https://www.ies.org/product/ies-spatial-daylight-autonomy-sda-and-annual-sunlight-exposure-ase (accessed 28 December 2024).
2383-8701/© 2025 The Author(s). Published by solarlits.com. This is an open access article distributed under the terms and conditions of the Creative Commons Attribution 4.0 License.
 HOME
HOME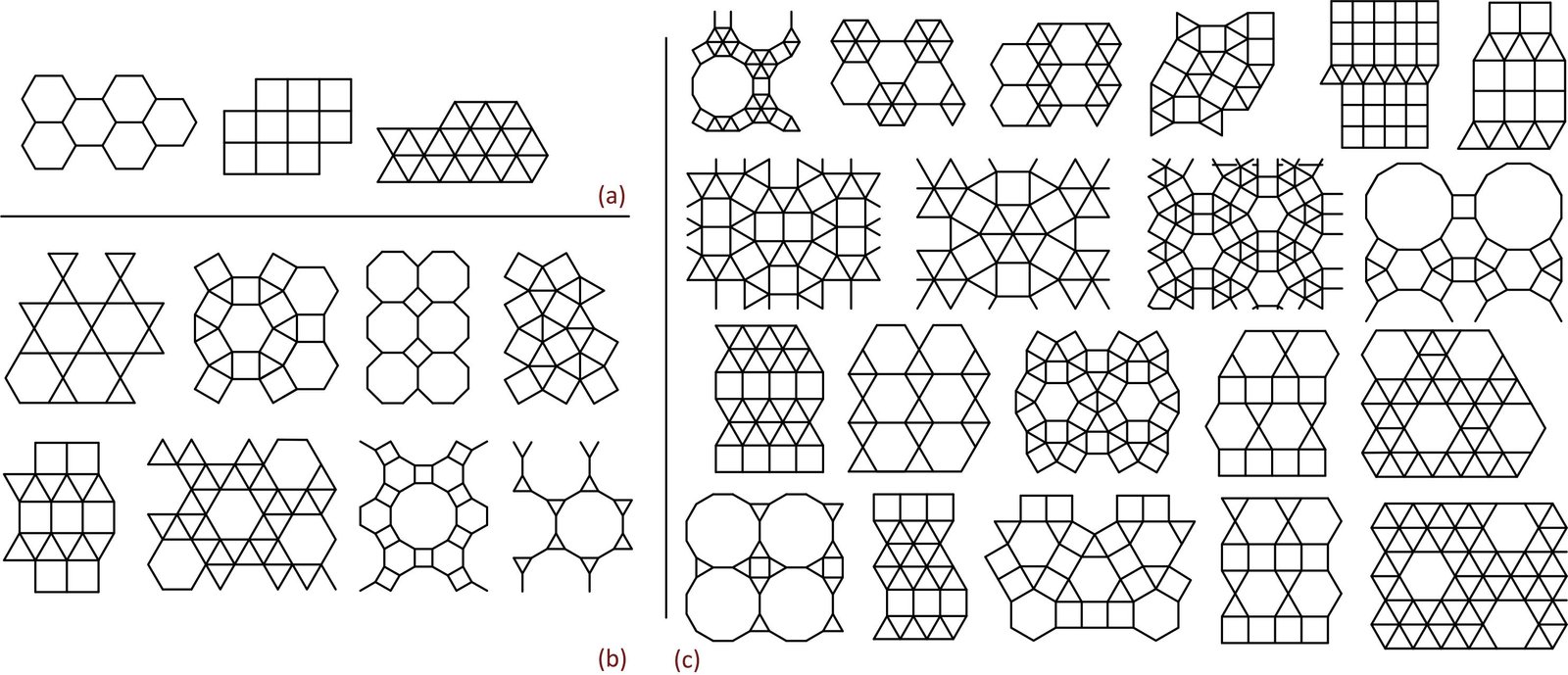 Figure 1
Figure 1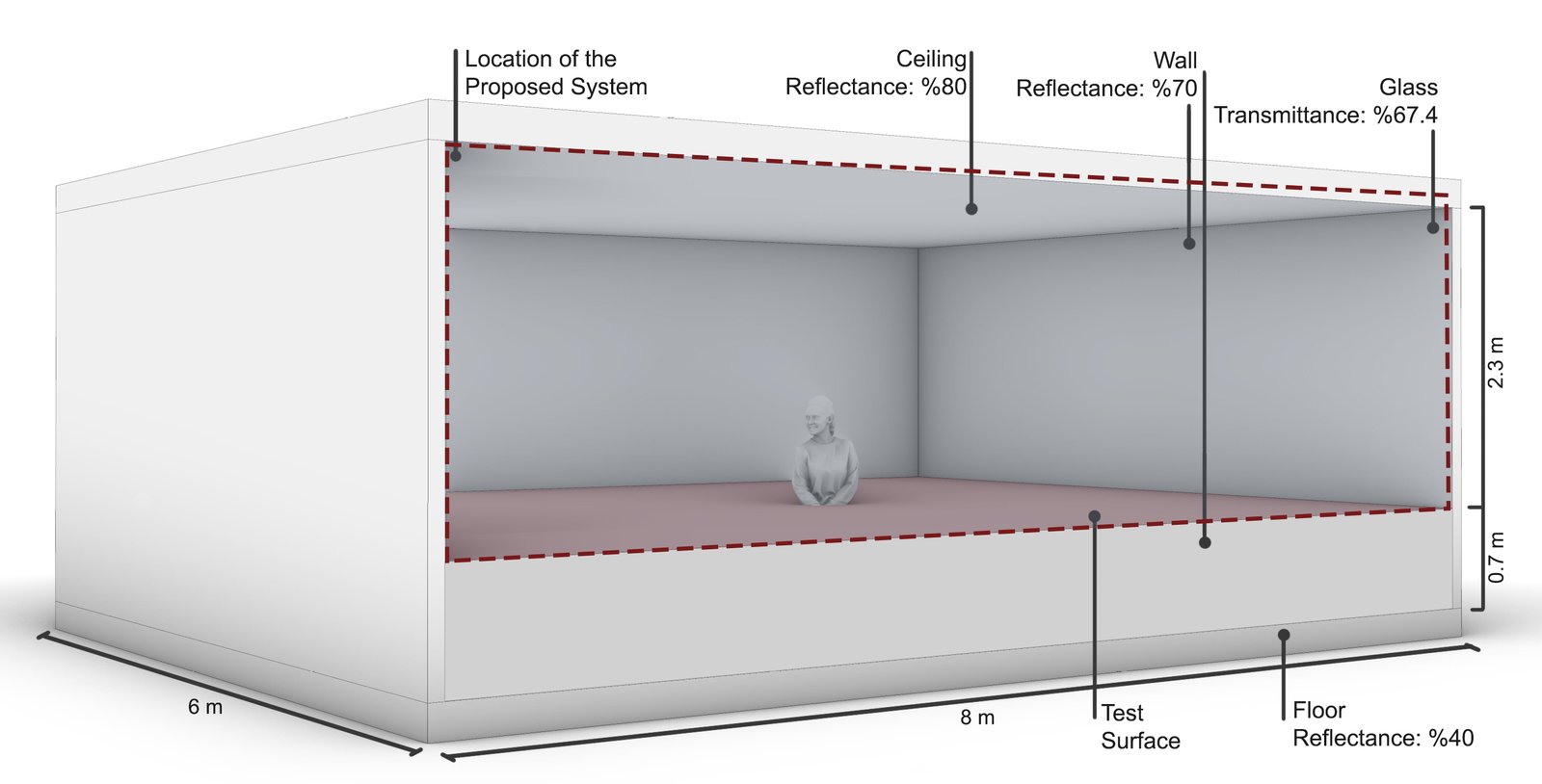 Figure 2
Figure 2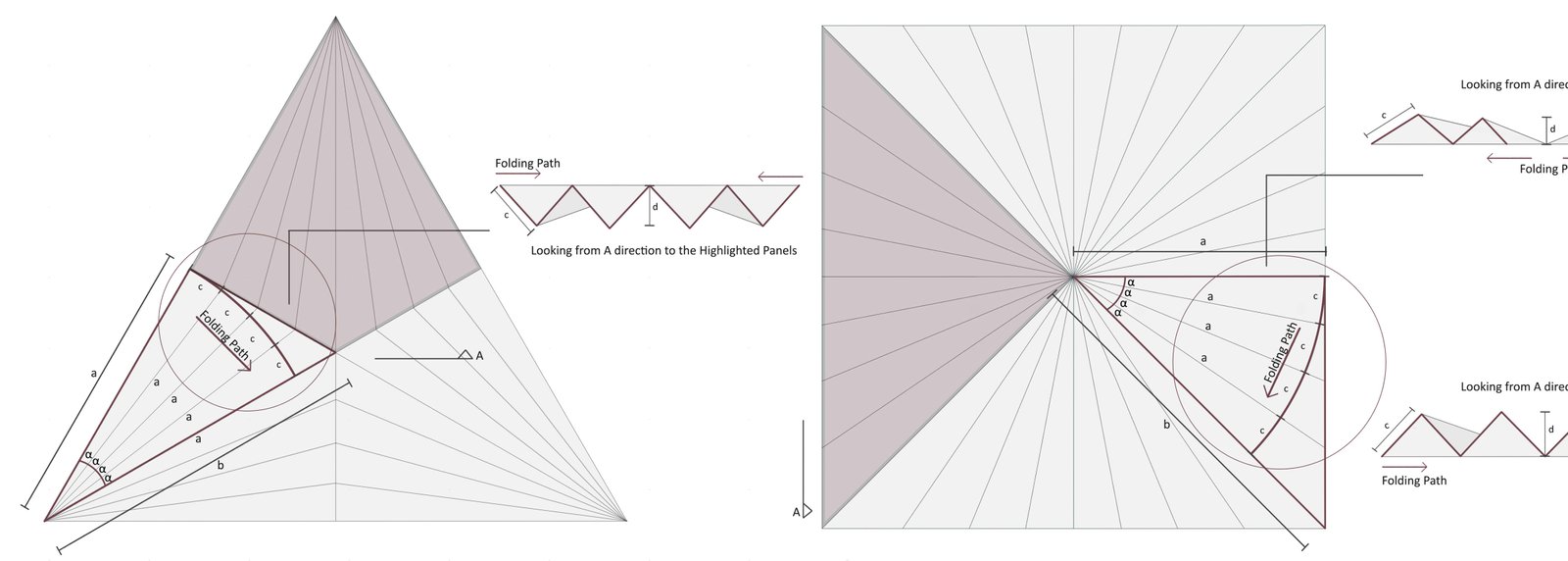 Figure 3
Figure 3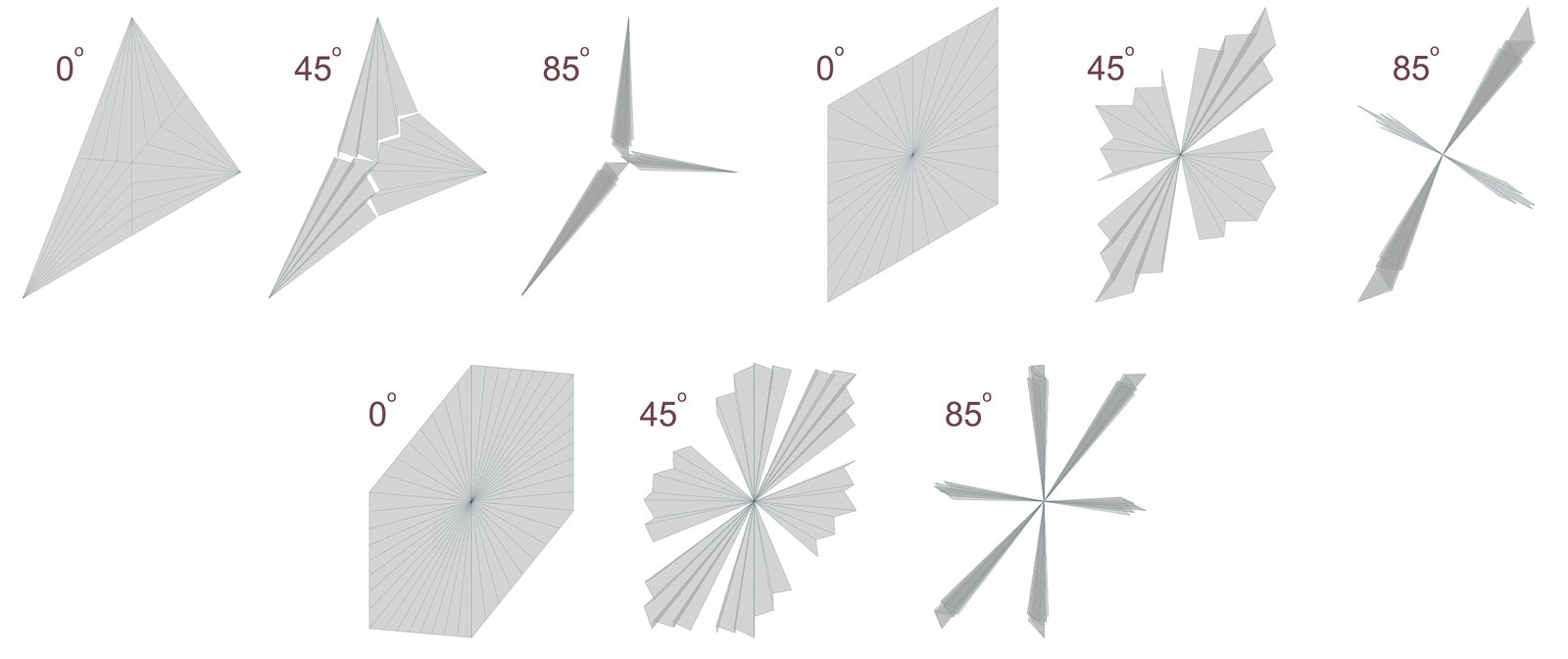 Figure 4
Figure 4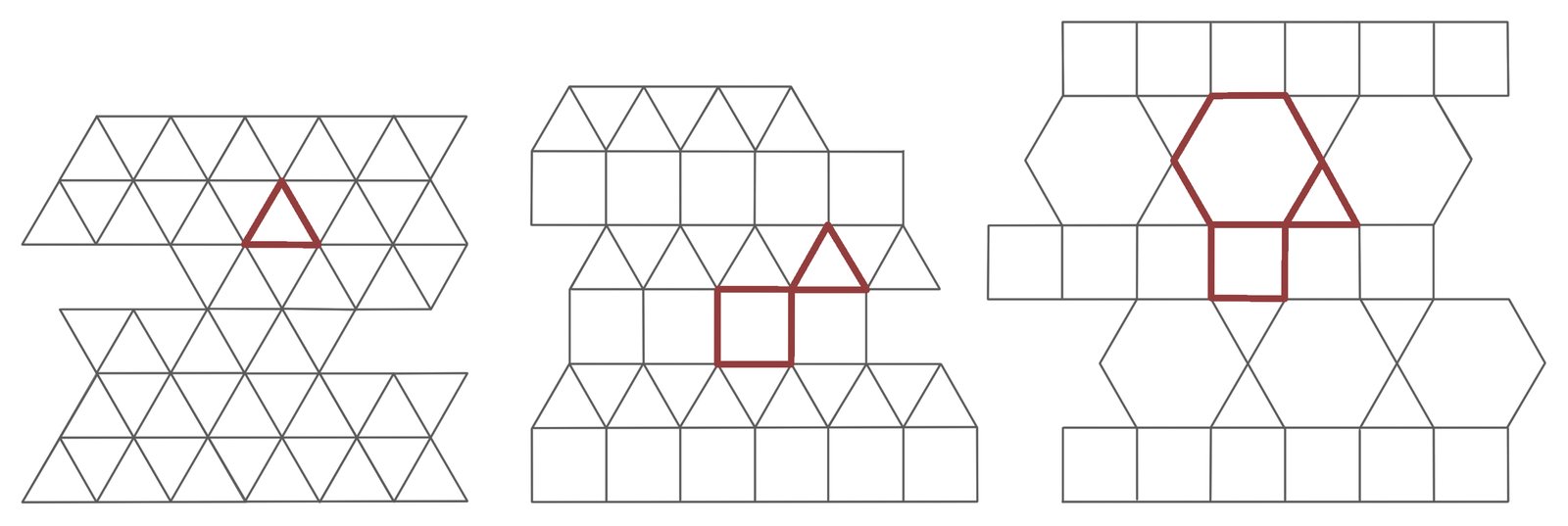 Figure 5
Figure 5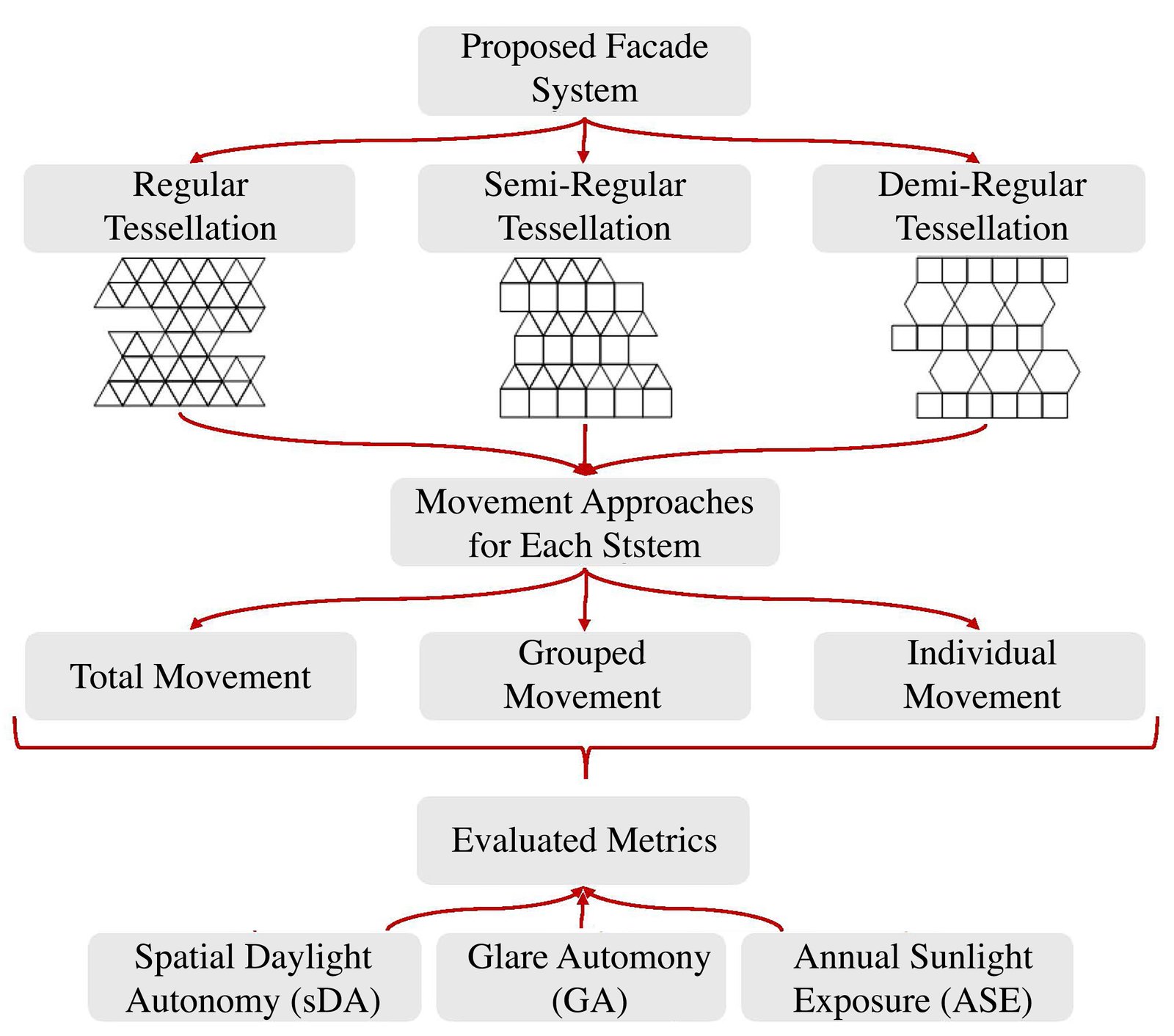 Figure 6
Figure 6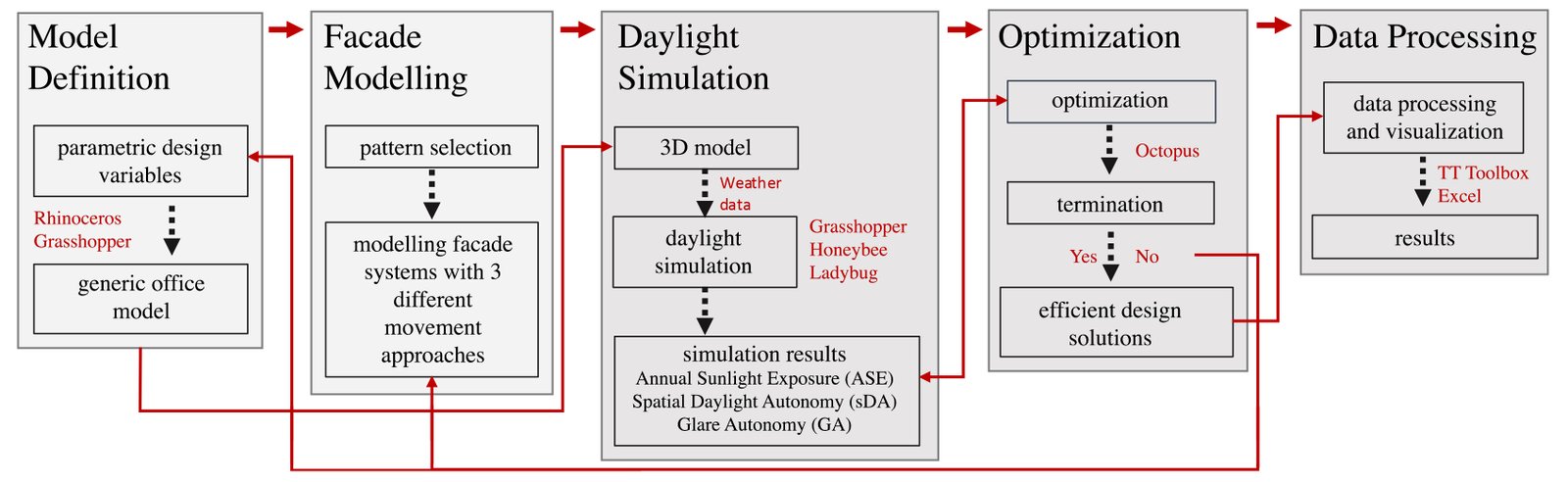 Figure 7
Figure 7 Figure 8
Figure 8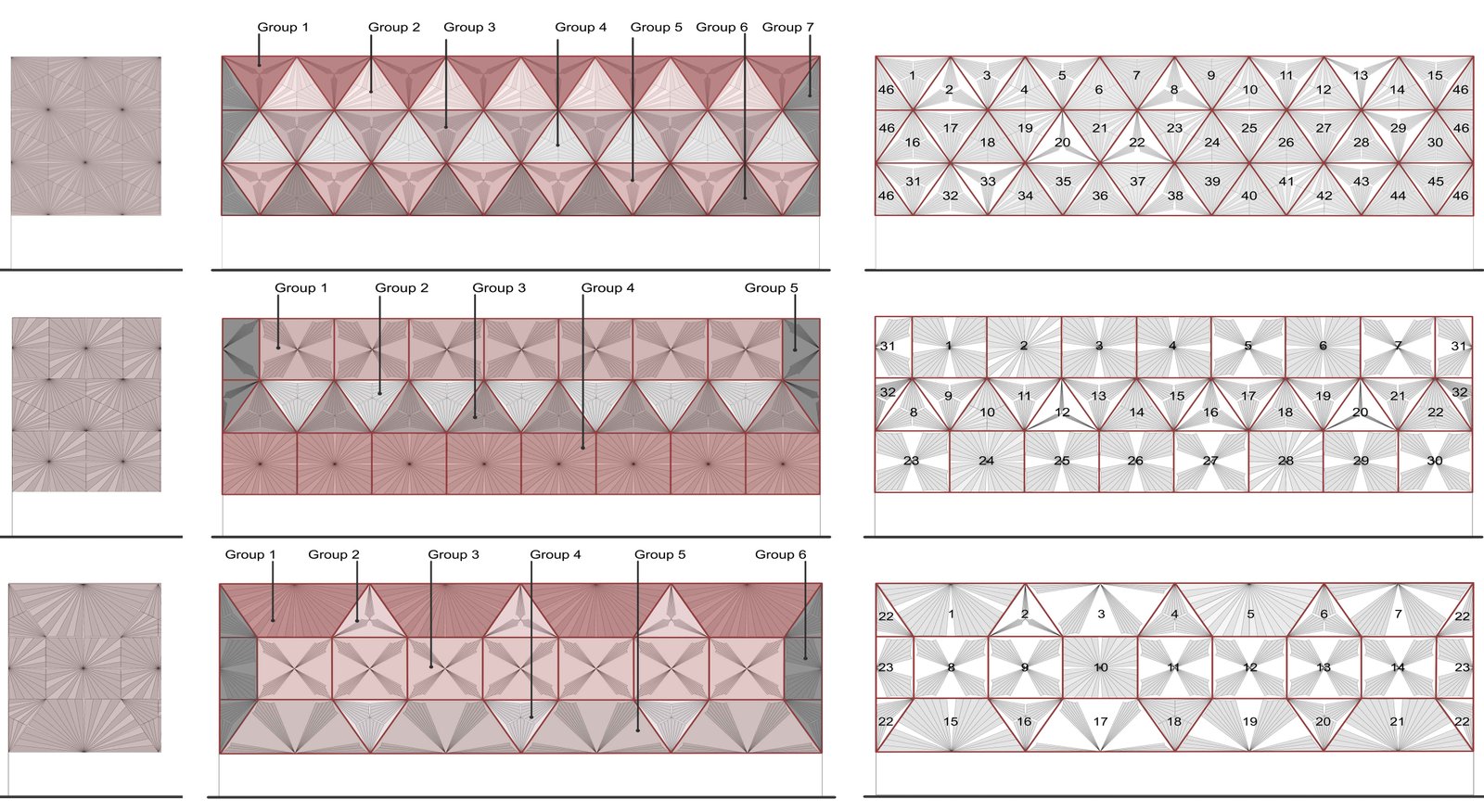 Figure 9
Figure 9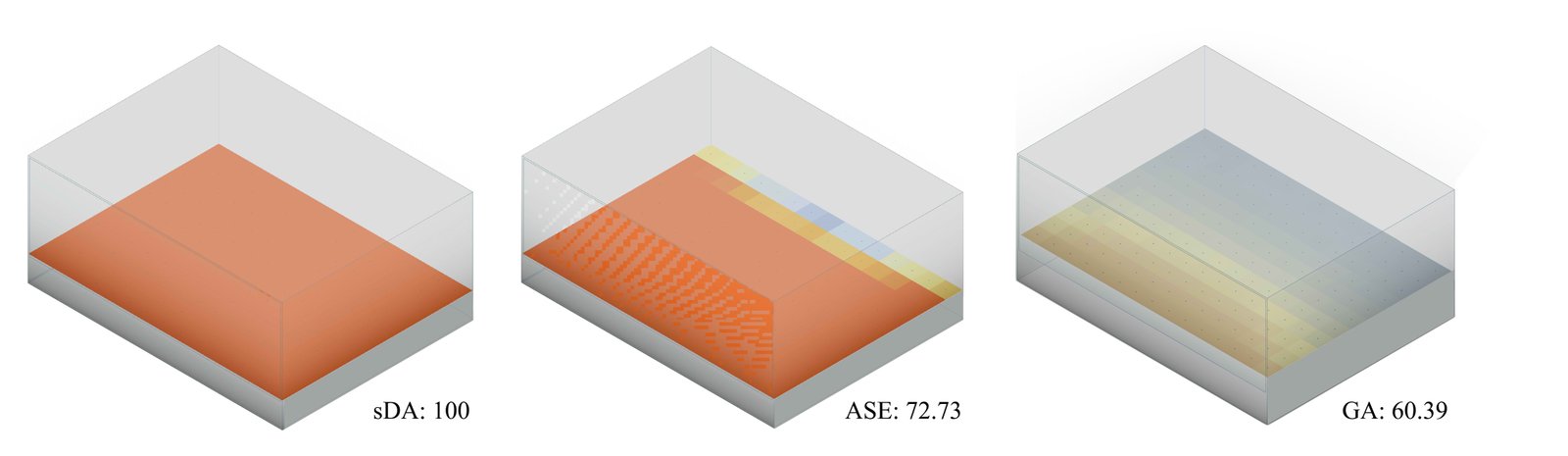 Figure 10
Figure 10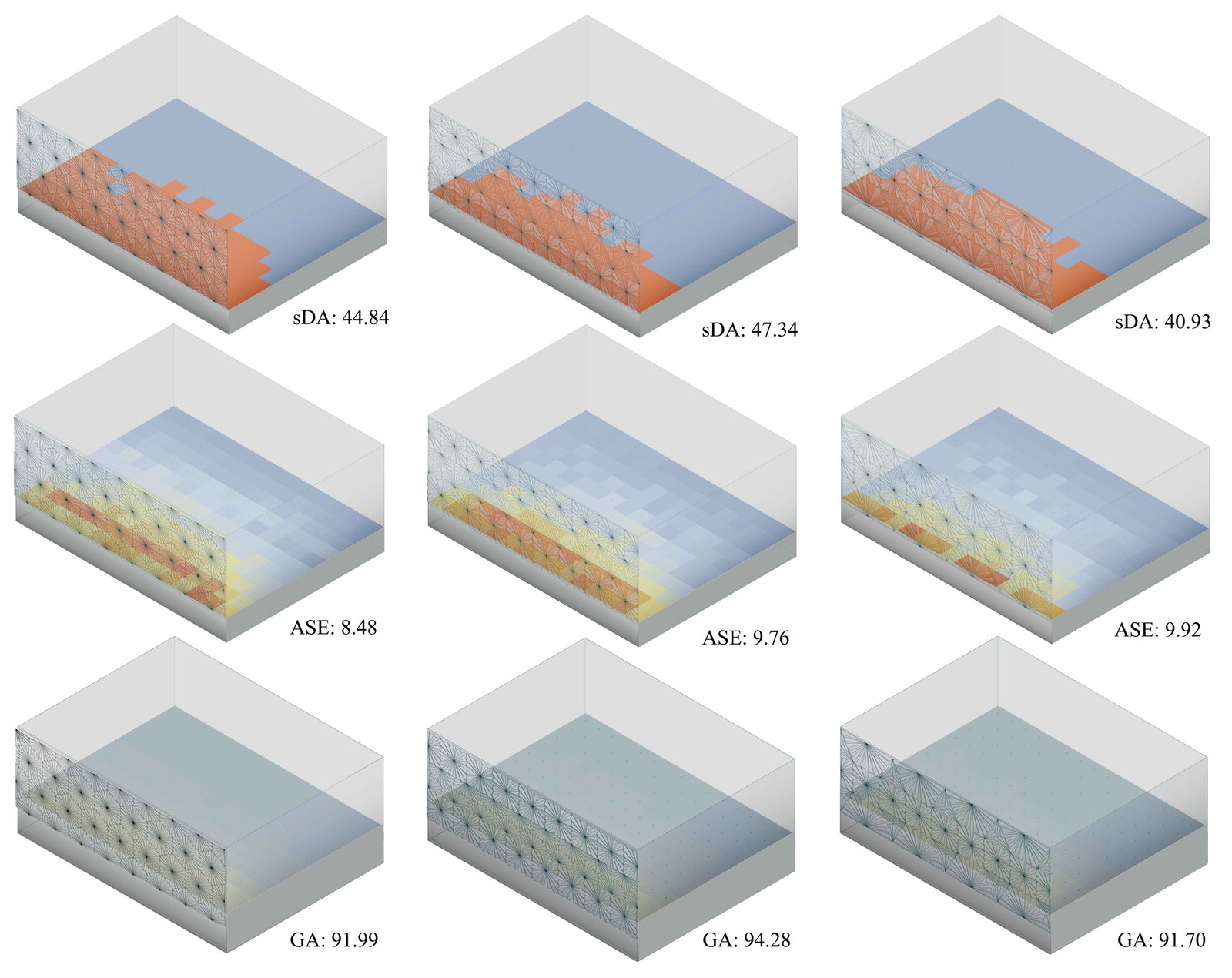 Figure 11
Figure 11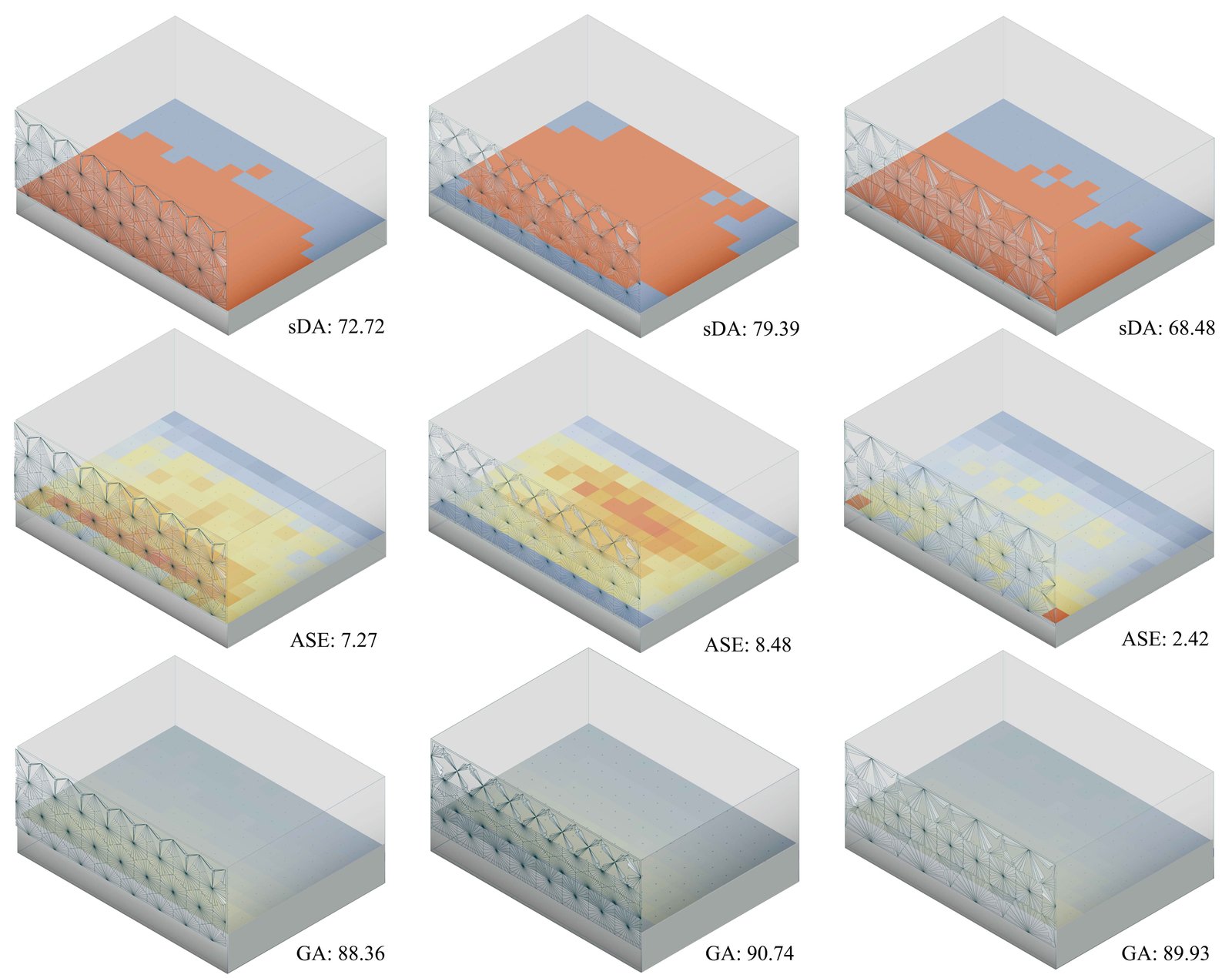 Figure 12
Figure 12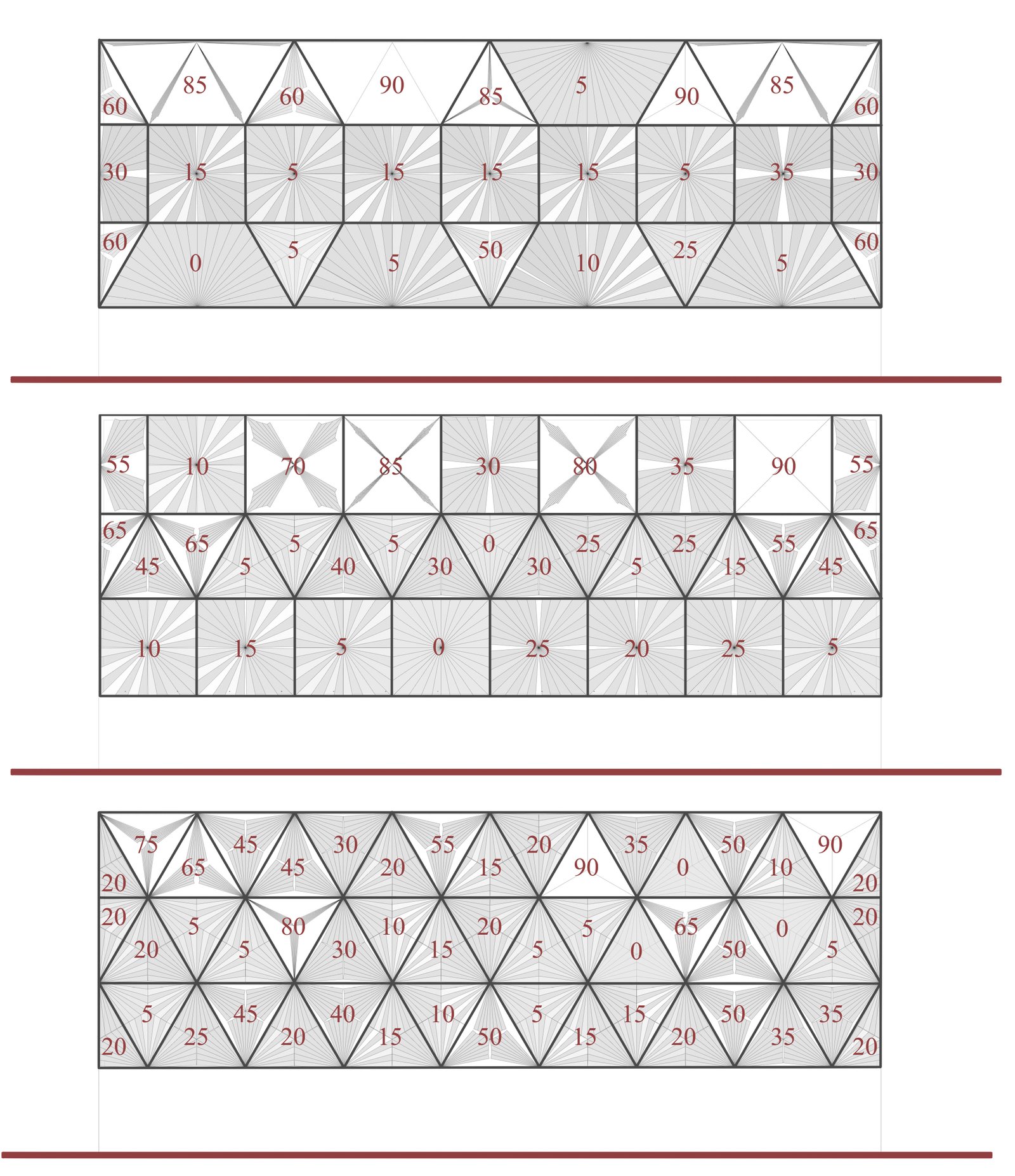 Figure 13
Figure 13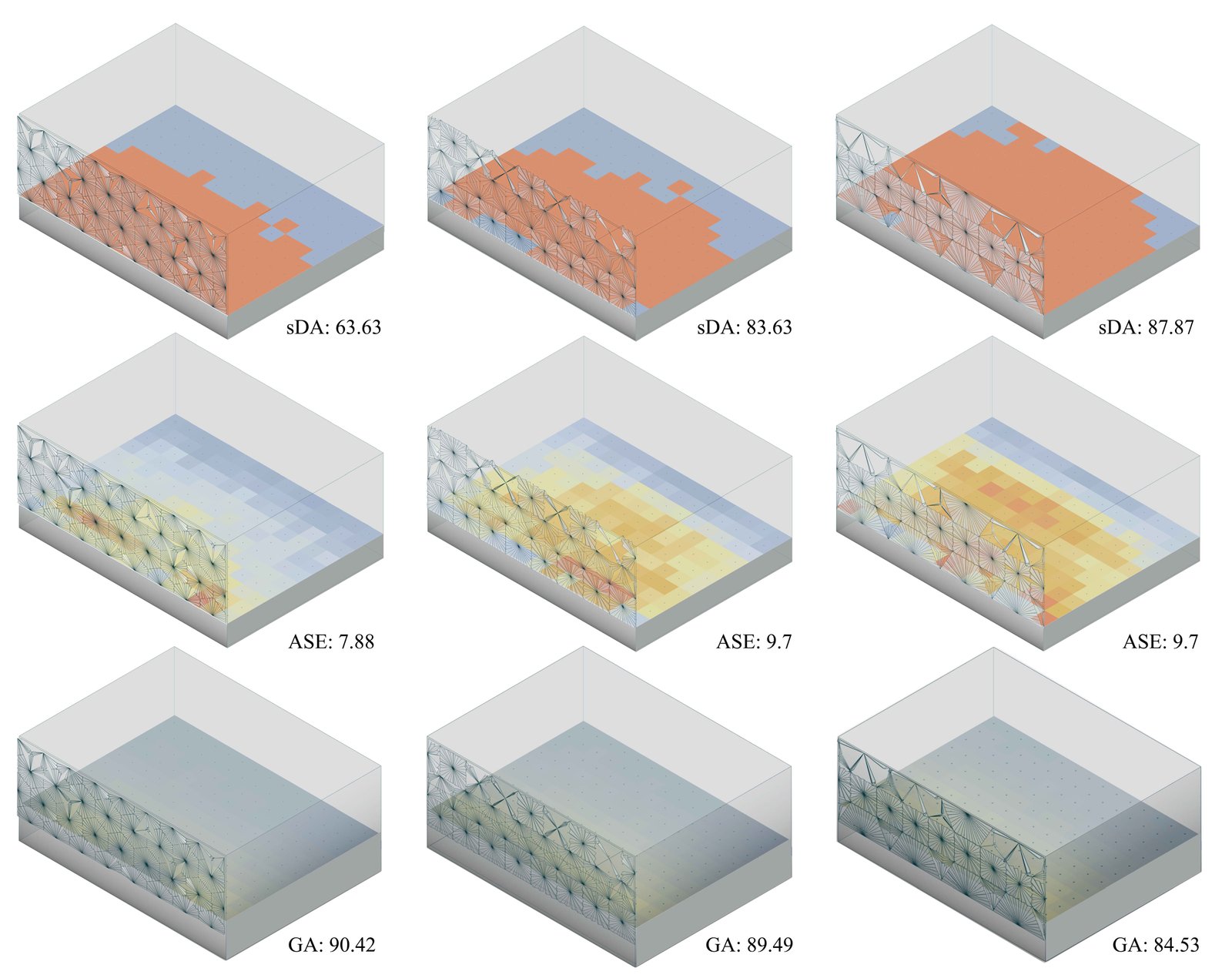 Figure 14
Figure 14 Table 1
Table 1 Table 2
Table 2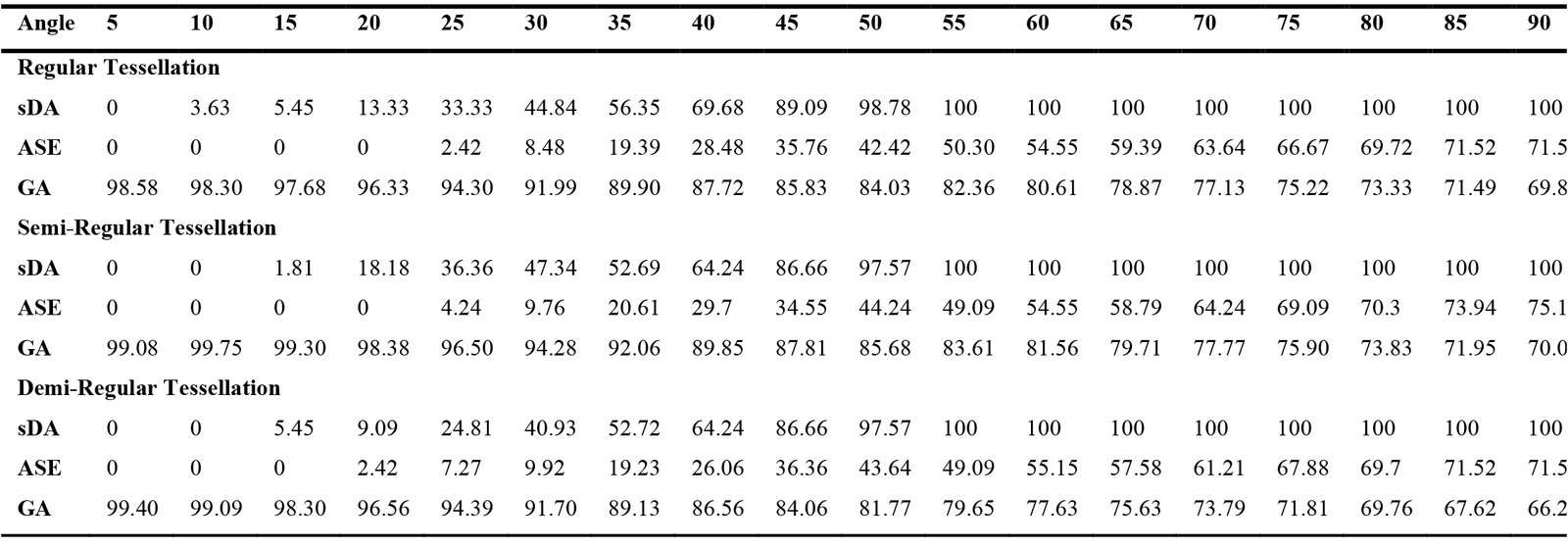 Table 3
Table 3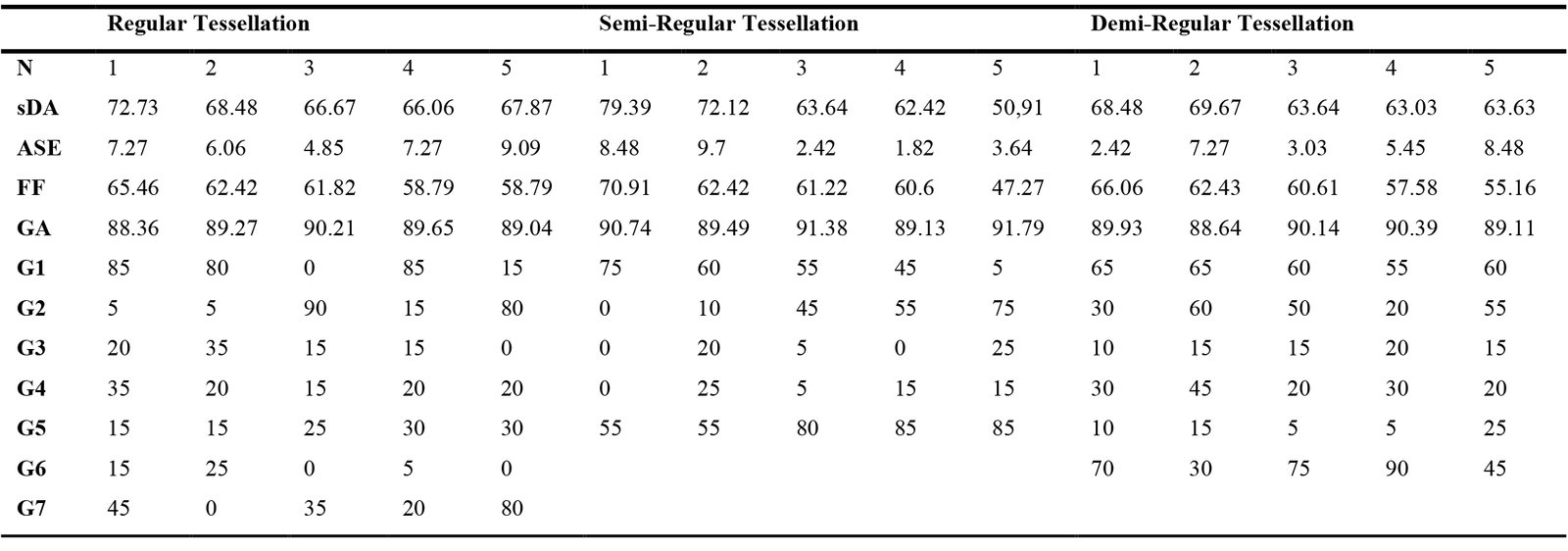 Table 4
Table 4


