Article Outline
4. Validation: physical scaled-model test
5. Input variables: modeling and parameters design
Declaration of competing interest
Figures and tables
Volume 7 Issue 1 pp. 122-136 • doi: 10.15627/jd.2020.10
Optimization of Daylight Performance Based on Controllable Light-shelf Parameters using Genetic Algorithms in the Tropical Climate of Malaysia
Ali Ahmed Salem Bahdad,* Sharifah Fairuz Syed Fadzil, Nooriati Taib
Author affiliations
School of Housing, Building, and Planning, Universiti Sains Malaysia (USM), Penang, Malaysia
* Corresponding author.
alibahaddad@gmail.com (A. A. S. Bahdad)
sfsf@usm.my (S. F. S. Fadzil)
nooriati@usm.my (N. Taib)
History: Received 30 April 2020 | Revised 5 June 2020 | Accepted 15 June 2020 | Published online 20 June 2020
Copyright: © 2020 The Author(s). Published by solarlits.com. This is an open access article under the CC BY license (http://creativecommons.org/licenses/by/4.0/).
Citation: Ali Ahmed Salem Bahdad, Sharifah Fairuz Syed Fadzil, Nooriati Taib, Optimization of Daylight Performance Based on Controllable Light-shelf Parameters using Genetic Algorithms in the Tropical Climate of Malaysia, Journal of Daylighting 7 (2020) 122-136. https://dx.doi.org/10.15627/jd.2020.10
Figures and tables
Abstract
This study aims to achieve a balance of daylight availability in the work-plane environments of a fully glazed facade integrated with a light shelf system using an optimization procedure that can assist architects with assessing the daylighting performance of numerous design alternatives, and build-up the optimized design. The approach uses parametric design, simulation modelling, and genetic algorithms. A case study of a typical office is carried out to test and verify the effectiveness of the optimization procedure for a light shelf system. Five parameters of light shelf design are optimized in two solar solstices (June and December) and one equinox in March under the Malaysian sky conditions. The optimization results indicate that the optimal design options of light-shelf parameters have great potential for illuminance improvement. After the optimization, the daylighting performance of useful daylight illuminance compared to reference models is increased respectively with an average value of 15.6% and 4.7% on the 21st of June, and by 17.5% and 5.8% on 21st of March, and by 5.8% and 11.3% on 21st of December. Statistical analysis is achieved to investigate the relationship between the performance metric of the optimal design options and the other cases, the outcomes showed that the regression analysis indicated a high level of reliability as well as different levels of variation coefficients.
Keywords
Daylight performance, Parametric simulation tools, Genetic algorithms, Light-shelf
Nomenclature
| GA | Genetic algorithm |
| DA | Daylight autonomy |
| UDI | Useful daylight illuminance |
| DR | Daylight ratio |
| RGB | Reflectance value of (red, green, blue) |
| BC | Base case |
| FC | Fixed case |
| OPTs | Optimized options |
| PH | Position height of light-shelf |
| EDR | External depth ratio of light-shelf |
| IDR | Internal depth ratio of light-shelf |
| EPA | External part angle of light-shelf |
| IPA | Internal part angle of light-shelf |
| R2 | Regression analysis |
| M | Mean values |
| Std | Standard deviations |
| V | Variation coefficients |
1. Introduction
Sustainable architecture design is a complex combination process that requires the reconciliation of buildings, occupant requests, and ecological boundary conditions [1]. Daylighting is one of the most significant components of the environment that needs to be considered in order to provide an appropriate interior environment, as well as achieve energy efficiency and other sustainability outcomes. Due to the special needs for daylighting in interior work environments, it has become imperative to state that, the entrance of sunlight is valuable in creating a healthy, comfortable, and productive work-place [2]. Nevertheless, the investigation of daylighting in workplaces has been a subject of interest for a long time. Natural light has assumed a pivotal function in the design of interior work environments, even more than in the design of any other building type [3]. A suitable design is expected to allow the right quantity of natural light into space and guide the entering light such that it creates a balance in daylight. The main purpose of such designs is to control the amount of inbound daylight [4].
Bringing natural light to buildings is, therefore, one of the most important aspects of design. Designing for the optimal level of natural light that gets inside a building is complicated by many factors that may affect the distribution of light. The typology of the building and its possible impact on optimum daylight rates in its internal areas is one of these criteria [5]. Bringing natural light to buildings is, therefore, one of the most important aspects of design. Designing for the optimal level of natural light that gets inside a building is complicated by many factors that may affect the distribution of light. The typology of the building and its possible impact on optimum daylight rates in its internal areas is one of these criteria [6]. Thus, in the design process of a well-lit workspace environment, both the quantitative and the qualitative criteria must be met. However, in the daylight system design of buildings especially offices, where occupants typically cannot change their positions and have restricted visual comfort choices, problems regularly occur in achieving the harmony between sufficiently well-lit spaces from the window and its undesired illuminance (under-lit and over-lit). In addition to that, the introduction of natural light in an interior adds complexity to the previous problems, especially in the tropic regions such as Malaysia, due to its dynamic nature, since daylight design requirements have to counterbalance useful daylight adequacy through the working hours [7-9].
Nowadays, it has become a regular practice to design tall office buildings with exteriors having vertical large glazing areas. This exterior facade pattern is visible in many nations around the world including countries in the tropics such as Malaysia. The utilization of large glazing surfaces offers numerous architectural benefits and even psychological advantages [10]. However, previous researches have shown that the vertical large windows can, in most cases, adequately and viably provide daylight for a zone as far as five meters away from the window-wall [11,12]. Thus, it extends the day-lit daylight area with resizing the window to fully glazed facades and leading to a disproportional amount of sunlight (causing glare problems) into the front portion of the room, and normally little gains in daylight levels are accomplished at the back [9]. Therefore, to overcome and control those obstructions, some controlled daylighting systems have been adopted to improve daylighting performance inside buildings; e.g. light-shelf, louvres, light pipes, fibre optics, Venetian blinds, and other complex daylight systems [3,13-16]. Daylighting systems are integrated in buildings that provide high-quality illumination. Daylighting systems ought to be simple and cost-effective to follow the needs of the market [17]. However, the correct design and determination of daylighting systems can fundamentally help in improving natural illuminance performance [18].
One of the most effective daylight devices to control sunlight entering the indoor space is a light shelf. Light shelf plays a critical function in improving and controlling interior daylight performance, expanding the occupants' visual comfort. Its performances rely upon various parameters such as geometry, materials, dimensions, the inclination angle of the external portion of the device, external climatic conditions (overcast or clear sky, with or without the sun). The outer portion of the system is capable to shade the glass surface, while the inner portion reflects the sunshine, directing illuminance away from the window and produces a uniform distribution of light on the work-plane [19].
Recently, more attention is been given in the literature to the light-shelf as a technique for enhanced daylight flow, especially in the rear areas of the space. Many studies investigated utilizing the light-shelf which can divert daylight into buildings. But the light-shelf has the problem of changing sun attitudes and elevations, as well as, constantly changing sky climate conditions, as is the case in Malaysia. Nevertheless, the light-shelf can somewhat improve consistency and distribution at the rear of deep space. Besides, it can shield occupants from direct daylight in forwarding zones, and give visual contact to the outside at the same time [20]. Thus, a controlled light-shelf was chosen in this study to overcome all the issues addressed above.
To address the research problem, and to evaluate the proposed system, which is a controlled light-shelf, a daylighting simulation was been carried out using parametric modelling and analysis using simulation tools. Computational parametric modelling and simulation are becoming a fundamental tool that carries articulated generative strategies to form transformations in architectural designs. They act as a vehicle for the structure of design configuration models according to various connections of the design idea, and the design processes. It underpins investigations of building configuration concerning its performance using simulations and modelling tools for the adjustment and optimization of geometrical structures towards a proposed design [21]. Advanced parametric strategies enable the examination of a wide range of design expectations and the generation of alternative project arrangements. Therefore, a novel parametric methodology that coordinates climatic and site information into a unique model of a building project, to help architectural decisions in early design stages, is presented [22]. This method was chosen in this study due to worldwide confidence in their demonstrated reliability and accuracy of outcomes in researches [23].
However, there is still a gap and a lack of daylight parameters systems optimization studies in tropical climates that examines the daylighting performance using light shelf with parametric simulation and optimization methods. For example, in most previous studies, a set of optimum fixed solutions were resolved for the entire year, and this to a great extent conflicts with the atmospheric conditions of the tropics. In other words, once selected and implemented, the design variables are expected to stay unaltered, therefore, only one type of static light shelf system is not adequate to accommodate a day-to-day usage by offering optimum daylight efficiency [24]. Thus, the simulation is carried out in this study for multiple scenarios in a year and different times in a day, where multiple optimum solutions are expected for each scenario. It is therefore predicted that the design parameters will differ as to the sky situation changes and the time lag from one scenario to the other. This research aims at developing a framework for optimizing light shelf systems for designers and practitioners in the early design stage. This framework for optimization is composed of parametric design, integrated daylight simulation software, and genetic algorithms. The applicability of this optimization method is checked by the case analysis of office space and various light-shelf parameters.
The fully glazed facades and office spaces require the use of controlled daylight strategies to minimize the risk of over-lit areas and optimize the use of natural light during working hours. This paper describes a method of optimization combined with a simulation of daylight using a genetic algorithm. It refers to selected optimum design parameter values connected to office buildings in Malaysia's tropical climate, and their features are compared for enhancing the daylighting in an interior workspace.
2. Objectives of the study
The main objective of this study is to provide a reliable and efficient method of analysis and generalizable findings to maximize the efficiency of daylight utilization and applicable design solutions to minimize the unuseful daylight levels in office workspaces using the light shelf as daylight system. The current research aims to assure reaching a successful daylighting in terms of quantity and quality by using light shelf which can be adjustable to different tropical solar solstice conditions by controlling and modifications parameters.
3. Research methodology
3.1. Research framework
The adoption of simulation software to obtain building performance data is a common feature of research in the construction design process [25]. The approach that combines genetic algorithms and parametric simulation tools for optimization has recently become a popular method for building performance analysis. Advanced parametric processes allow a wide variety of design intentions to be explored and alternative project configurations generated [22]. Nowadays, the use of parametric modelling and optimization algorithms through evolutionary computation has become more common to determine the optimum solutions in construction design. The method in this study combines optimization algorithms and simulation tools.
As shown in Fig. 1, the research framework of this study employs a parametric daylighting design method using Radiance which developed in Rhino/Grasshopper and Ladybug and Honeybee plug-ins. The incorporation of these tools was necessary to achieve the objectives of this study: Rhino as a modelling tool, Grasshopper as a parametric interface, and Ladybug and Honeybee tools for daylight analysis application using Radiance. For organizing the research flow of this study, the framework beginning with building a parametric design model with side-lit south-facing and identifying the light shelf design variables to be examined in the first step. The second step is the development of the daylight model with Radiance parameters. The third step is multi-objective optimization using genetic algorithms embedded in the Galapagos tool included in Grasshopper. Following the completion of the optimization, the simulation data and optimized design solutions are further evaluated in the final phase.
The optimization process starts with Rhinoceros 3D modelling software and its Grasshopper parametric modelling plug-in. The geometry of the building is built with all the predetermined light shelf parameters, the values of which can be modified via sliders. The context of each design element is determined by the expertise of the designer. Daylight and climate data functions are provided by Ladybug and Honeybee. In the daylighting modelling process, the parametric geometry of the building is connected to the materials component in the Radiance program with the setting of material transparency, reflectance, etc. The building materials are then linked to the daylighting simulation component, with the input of weather data, the location of daylight sensors placement, and other simulation settings. Ladybug imports simulation tests file back into Grasshopper after the simulation has finished.
3.2. Optimization process
In the field of building performance simulation, numerous optimization approaches have been used to solve single and multi-objective problems. Numerous studies in the areas of the Multi-Objective Modeling problem in the literature have been published so far. Therefore, a GA has become very common as types of optimization algorithms. The GA is commonly used in the field of multi-objective performance optimization by combining technologies for parametric modelling platforms [26,27]. The utilization of GA to solve optimization issues is sensible and likely successful in finding the best solutions in a relatively short computational period [9]. Optimization is the way towards finding the minimum or maximum value of a function by choosing several constraints in several variables [28]. In this study, the optimization process is a multi-objective optimization, which has been carried using the GA embedded in the Galapagos tool included in Grasshopper as shown in Fig. 2. The Radiance daylight engine was used connected with a GA (Galapagos) to search for high-performance light shelf parameters for UDI.
Two generally utilized sky types for daylighting simulations depend on the CIE sky model and the Perez sky model. These models are essentially mathematical equations that calculate the continuous luminance distribution of the celestial hemisphere as a function of variables such as geographical location, time and physically measured radiation data [29]. The optimization was carried out under CIE Intermediate Sky conditions, as the tropical sky is predominantly intermediate as mentioned by previous studies [30-32], which indicated that more than 85% of weather conditions at tropical areas are of intermediate sky condition [24]. Thus, daylighting simulation studies in the tropics such as Malaysia shall consider the intermediate skies [24,33-36].
3.3. UDI
Dynamic daylight metrics have been advanced in keeping the researchers informed of the annual measurements of illuminance, where calculations are processed throughout the year and based on the weather data of the study's geographic location [21]. The DA [37] and UDI [38] metrics have recently been commonly utilized under various conditions, and both have proved effective in evaluating the daylight efficiency of an architectural room [39-42]. These metrics use annual simulations to determine the percentage of daylight at a given sensor node according to an appropriate illumination level [21].
DA is defined as ‘the percentage of the occupied hours of the year when a minimum illuminance threshold is met by daylight alone’ [43]. DA defines visual performance through one single value and shows how far daylight will penetrate space [21]. Proper daylight autonomy value is usually considered when a specified illuminance level (300 lx) for occupancy is over 50% (in short, DA300,50%) [44,45]. UDI largely resembles DA but defines lower and upper illuminance thresholds (UDI=100-2000 lx) for daylight to be “useful”. UDI measures the percentage of work area at least 50% of the occupied hours that meet an illuminance range of 100 lx and 2000 lx [9,44,46,47]. UDI also shows the levels of daylight correlated with occupant discomfort (i.e. glare problems) and excessive solar gain based on the horizontal illuminance level [48]. The lower and upper levels of UDI thresholds are divided by the annual illuminance distribution into three levels; the upper threshold (UDI>2000 lx) presents the time when an oversupply of daylight happens, which could lead to visual and thermal discomfort; the lower threshold (UDI<100 lx) presents the time when there is insufficient daylight and the middle threshold (UDI 100–2000 lx) presents useful daylight [49]. In a later study by Mardaljevic and others, they further subdivided the 100-2000 lx “useful” UDI thresholds into a “supplementary” (100-500 lx) and an “autonomous” (500-2000 lx) level [41]. A study by Pool [50] defines the UDI thresholds between 150lx to 3000 lx, and further subdivided the UDI thresholds into a “non-sufficient” (UDI<150), UDI 150-300 lx to show the transition time between unuseful range and useful range, “autonomous for the task” (UDI 300-3000 lx), and UDI >3000 lx to represent the times in which the daylight might be excessive, causing overheating or glare problems.
Both DA and UDI consider that the fraction of working hours throughout the year has met the target value (minimum value in the case of DA and range in the case of UDI) [45]. To better describe an architectural space instead of one given point, to consider whether space receives sufficient daylight, UDI scheme was used, which is a widely adopted dynamic metric for daylight availability assessment to determine how much space is receiving adequate daylight, and allows the verification of the frequency of occurrence of predetermined illuminance ranges. This metric is complementary to daylight autonomy, and in this research, the energy savings and glare were ignored in the analysis results.
Malaysian standard (MS 1525:2014) [51] and Green Building Index (GBI NRNC), as well as standards of Japan (JIS Z 9110) [52], and South Korea (KS A 3011) [53], the minimum recommended daylight illuminance of office spaces at the work-plane is equal or more than 300 lx, and the maximum acceptable UDI range as mentioned previously is 2000 lx, so the useful daylight illuminance in this study, is defined where all the illuminances are within the range 300lx to 2000lx. For this research, each range set of UDI values were sorted into one of these three categories: Under-lit UDI<300 lx, Day-lit UDI300-2000 lx, and Over-lit UDI>2000 lx areas. These three thresholds of UDI values were used in this research to the performance comparison of different light shelf parameters to optimize the best light shelf parameters design for office spaces.
3.4. Simulation data set: date, time, and weather data
This study focuses to measure the daylight availability through optimising the design parameters of light shelves in an office space. In order to evaluate the trend of the selected parameters of light-shelf, simulations have been performed in critical days of Malaysian sky conditions and different times of daily working hours. The occupancy hours for daylight calculations were set from 08:00 to 17:00 assuming office use. To assess the trend of the selected daylight acquired from the performance criteria, parametric simulations and optimization for chosen parameters have been performed at; 21st of June (June solstice), March (equinox), and December (December solstice) in the year of 2019, at four critical times of daily office work; 09:00, 12:00, 15:00 and 17:00, which are represented respectively as four different sun angular in a day as shown in Fig. 3. These specific dates were chosen to cover all possible circumstances of daylight exposure, which represented the most critical climate conditions of the Malaysian sky sun path (see Table 1). Because the solar altitude is the highest on the June solstice and the lowest on the December solstice. The solar altitude on the equinox lies between the values on the June solstice and December solstice. Therefore, it can be useful to evaluate the impact of these three days with direct sunlight and diffused light. The conditions of these typical days made the performance investigation for the widest scope of solar altitude variations. Simulations were carried out under climate-based daylight. The climatic data of the reference standard year for Penang. The weather data file (EPW) for Penang, Malaysia, with data recorded at Penang international airport downloaded from the online website of ladybug tools/epwmap/ [54] based on EnergyPlus weather data file was used.
Figure 3
Fig. 3. Sun path on June 21st, March 21st, and December 21st and sun at 4 critical times of work hours.
4. Validation: physical scaled-model test
This study utilized parametric tools and optimization method based on Radiance simulation engine to compare with the field physical scaled-model measurements to validate the simulation results. The validation was done based on a previous study [31]. A 1/10 scale model (Fig. 4) and simulate model (Fig. 5) had the same dimensions of 5 m × 8 m × 2.80 m (width×depth×height) with the Window-Wall-Ratio was 40% [55] is modelled according to Table 2. The model was constructed with thin plywood. And all construction materials and interior surfaces (walls, floor, and ceiling) were painted white with reflectance (RGB = 0.84, 0.84, 0.84). The external envelope of the model was painted black with reflectance (RGB = 0.02, 0.02, 0.02) to block other sources of daylight apart from the single-sided external window, as well as to reduce glare and light reflection. The program Radiance Colour Picker in jaloxa.eu [56], is used to convert the colours into reflectance using RGB values (red, green, blue).
Figure 4
Fig. 4. Plan and vertical section and perspective of the scale model (all the dimensions are in m).
Figure 5
Fig. 5. Plan and vertical section and perspective of the simulation model (all the dimensions are in m).
All of the measurements for validation were conducted as same as in simulation on three typical days (21/06, 21/03, and 21/12) during office hours from 8:00 to 17:00 and the average of daylight ratio was taken for the calculation. A total of three different points was selected for measurements. Illuminance data were recorded in the scale-model using illuminance lux meter (Table 3), while a grid sensor 0.50×0.50 m was used in the Radiance model. Three illuminance photosensors and nodes (Li1/Node1, Li2/Node2, and Li3/Node3) between the Radiance model and the scale-model were compared. The sensors were placed inside each model in the middle of the space above the work-plane level at height 0.80m to measure the internal illuminance level. The first Li1/Node1 located at 1m from the wall window while the second Li2/Node2 was placed in the middle of the space, the last Li3/Node3 located at 1m from the wall behind it at the back of space as shown in Figs. 4 and 5. The experiments took place at in an open area without any unobstructed on the top roof of the main building of the School of Housing, Building, and Planning at USM (Universiti Sains Malaysia) in Penang, Malaysia.
Due to the huge variation between the external outdoor illuminance under the tropical sky and CIE skies, previous researches [24,35,57,58], pointed out that relative ratios are utilized for the tropical daylight assessment validation methods under tropics sky. Therefore, Daylight Ratio (DR%), was employed as a method to validate the Radiance simulation. Many studies demonstrated that the use of the DR% calculation method which is more suitable for tropics regions [24,58,59], using the Eq. (1)
where In.L indoor illuminance, and Ex.L external illuminance. The Validation with DR% was performed anyway to ensure no significant errors existed in the model due to the modelling choice. A clearer comparison was made by calculating the daylight ratio of the measured and simulated results. The min/max values of the average difference between the measured and simulated results at measure points at two different solstices and equinox were approximately -0.20% and -7.20% respectively. This result showed that is in good agreement with the validation results of previous research that had max DR% difference was 8.75% [31], which mean they are all under 10% [60]. In addition to the calculation of the differences, based on Kim and Chung’s [34] study, the Relative Error (RE) between the two results was calculated at each point using the Eq. (2)
where Mexp is the measured illuminance value at each measurement point and Msim is the corresponding simulated illuminance value calculated using Radiance. The min/max values of average RE between the measured and simulated results at measure points at the solstices (June and December) and equinox (March) were approximately -0.40% and -3.93% respectively. From comparison analysis, the results showed that the range of min/max differences and relative errors between simulation and measurement is less than 10%, which is an acceptable result as noted by previous studies [31,61]. The comparison results show that both simulation and field measurements almost have an identical pattern of behaviour if the minor difference is neglected. Overall, the result indicates the validity of the simulation method in terms of accuracy. In other words, the criteria used were reliable and acceptable for predicting internal illuminance. Therefore, the model is deemed valid and fit for further daylighting measurements.
5. Input variables: modeling and parameters design
5.1. Case studies: BC and FC
To illustrate the impact of applying diverse light shelf configurations variables on the daylight efficiency of the indoor spaces, simulating whole buildings can take a considerable amount of time and it is important to make a simplified model to save time. Thus, in this study, a typical south-facing office has been constructed as base case (BC) model with fully glazing facade (Window-to-Wall Ratio = 90%) with spatial dimensions of 5.00m (width), 8.00 m (depth) and 2.80 m (clear height) as illustrated in Fig. 6(a). The stated office height was selected because in Malaysian office buildings as most of the spaces are using false ceilings, it reduces the height into 2.70 m or 2.80 m according to the previous studies [24,58,61]. The model represents a typical ‘shoebox’ model [21], which is commonly used for conceptual design explorations, where the room depth of 8.00m corresponds to nearly three times the floor-to-ceiling height, and the large depth is chosen so that the impacts of daylighting remains visible for all variables variations under study.
Material properties from reflecting surfaces will significantly impact daylight performance and the reflectance of materials that affect the direction of the incident light. In simulation tools, accurate information on the materials used for internal surfaces is also fundamental [63]. As indicated by the IESNA lighting guides for indoor reflectance of space, the floors give an auxiliary foundation to work-planes. In this way, the floors ought to have non-specular surfaces, with 20%-50% reflectance. The walls ought to likewise have non-specular surfaces, with 40%-70% reflectance. The ceiling ought to be as almost white as practicable and non-specular, with 70%-90% reflectance, for this surface is the most significant in reflecting daylight downward toward the work-planes [34]. To evaluate the daylighting performance in this research, thus, the material properties of office surfaces were treated as perfectly diffuse with typical visible reflectance values of materials of the ceiling, walls, and the floor was assumed as shown in Table 4. The surface material properties were defined in Honeybee-for- Grasshopper plugin, by embedding the red, green, blue (RGB) reflectance values, specularity, and roughness in 3D Radiance model. These selected surfaces materials properties were utilized because they represent an ideal office design [24,62]. In Malaysia, the most glazing frequently used are 6mm thick glass with visible transmittance from 20% to 80% [64]. However, the previous studies used different type of glass transmittance, for example; study by Lim et al. [35]; the transmittance used based in real buildings were 52% and 53%, while the study by Lee. S and Lee. K [65], as well as a study by Tabadkani et al. [66]; the visual transmittance of glazing was 65%. Thus, in this study, the transmittance of the window was assumed with a visible transmittance of 60%.
Specularity is fundamentally the ratio between specular and total reflecting components from material in the concept of material modelling in the radiance. If the non-zero material has red, green, blue reflections (R, G, B), then the total reflexity can be calculated. Meanwhile, roughness is the root-mean-squared facet slope of the material surface. This term refers to microscopic surface roughness; materials with more jagged facets tend to yield more blurry reflections and thus have higher roughness values. A perfectly polished surface has no ruggedness, while an unpolished surface, depending on the type of material, can have up to 0.20. It is highly unlikely for any material to have a roughness greater than 0.20 (i.e. is mostly close enough to zero) [67,68], therefore it is not significant to be optimized in this study. However, the Reflective, specularity, roughness, and transmittance properties may range in value from 0-1. Reflectance determines what proportion of light is reflected back from the surface, specularity determines the ratio of specular reflection to diffuse reflection, roughness determines the scattering of reflected light and transmittance determines what proportion of incident light is transmitted through the surface [69]. The surface specularity and roughness were proposed according to recommendations and previous researches [2,6,62,69,70].
Additional to the Base Case (BC) model, a light shelf was proposed to be installed as shown in Fig. 6(b) as a FC option to be improved by the optimization process. According to the previous studies [3,71,72], It is recommended that the light shelf be a combination of an external and an internal light shelf at a height of 1.80 m above the floor, with external and internal depth ratios 0.50m. Furthermore, putting a light shelf so high (more than 2,35 m above the floor) is considered reducing the distribution of daylight. The internal part, which the occupants can see, may or may not affect their visual experience; but more critically, can contribute to veiling reflection glare [2]. Each of the light shelf parameters was thus independently controlled for the exterior, and the interior sections in subsequent simulation runs were optimized using simulation with the GA technique.
The simulations were performed using the Radiance simulation engine. Several studies have confirmed the accuracy of the Radiance simulation engine and the simulation method [37,62,73]. To increase the accuracy of the simulation outcomes, the simulation parameters were set to use for all daylight simulations based on most previous daylight simulation studies. The suggested computational simulations settings and configurations for the reference office model parameters are listed in Table 5. For daylight simulations, an analysis grid test points (nodes) were created in Honeybee plugin in Grasshopper, which is used as an engine to stimulate Radiance simulation. The test nodes were set at the working-plane is positioned at 0.80 m height above the ground and is divided into a grid. The grid-scale of test nodes was set to 0.5m as mentioned above based on previous studies [7,74-79], i.e. four points each square meter, which resulted in 160 analysis nodes being used in the model to represent the illuminance value of each point as illustrated in Fig. 6.
5.2. Parameters selected of light-shelf: OPTs
This research focuses on the optimization of the most fitting daylight guidance system, which is the light shelf, in this case, to be placed on the south façade of the building. According to many design parameters of light shelves can be effected on the performance of daylight. Lee [80] pointed out the key parameters which determine the light shelf's performance including its angle, width/depth ratio, height, and reflectivity. This study tested different parametric designs of light shelf configuration with minimum/maximum and interval values of different variables: PH, EDR, IDR, EPA and IPA as shown in Table 6.
In the research carried out by Meresi [3], the light shelf width, and the tilt angle was respectively varied within an interval of 0.20 m and 10°. In the paper of Moazzeni and Ghiabaklou [72], the width was varied within an interval of 0.30m, and the tilt angle was tested for the values of 0°, 5°, 10°, 20°, and 30°. In the study of Joarder el at. [71], the height position was varied within an interval of 0.20 m, and, the minimum and maximum height position of the light shelf was assigned to be 1.50 m and 2.75 m, with external and internal part depth ratios were 0.50m. In this current study, smaller intervals were assigned to yield more accurate results, i.e. 0.10 m, 0.25 m, 0.25 m, 10°, and 10° respectively for the PH, EDR, IDR, EPA, and IPA. According to Littlefair [81], the width of an outer part of the light shelf should be more or less equal to the distance between the work-plane and the light shelf. Since there is a 0.50 m wide overhang on the fixed case was examined, the maximum width of the external light shelf was assigned to be 1.50 m, giving conceivable space for reflecting the daylight. The maximum internal width was set to be 1.50 m, thereby allowing the occupant less visual disturbance. Since the external and internal portion of the light shelf can be of controlled angles, a positive and negative angle is assigned to be +30° to -30°.
6. Results and discussion
Once the geometry office model and parameters of light-shelf are built and designed, the next step is evaluating its performance, simulation and optimization results are obtained in terms of illuminance performance. Thus, the UDI metric was used to analyze the illuminance performance inside the room by calculated the nodes (160 visible nodes) illuminance levels and percentages under three UDI thresholds, to have a detailed comparison. To guide simulations towards optimal design solutions, the optimized process was set to maximize UDI 300-2000 lx. The optimization process was run for 6125 cases for each selected date and time separately. Optimization with GA in Galapagos was run for 100 generations to find the optimal solutions that were approached. The optimization process resulted in a range of successful solutions that better enhance the performance of light-shelf regarding daylight performance with keeping illuminance levels within the max accepted range for UDI during test hours compared to other cases. To facilitate detailed analysis and interpretation, only the best options for selected dates and times were presented (12 options), and their geometries and UDI thresholds illuminance distributions on the work-plane are shown in Fig. 7 concerning light shelf parameters, the optimized values are more diverse, the Details values of design parameters in all GA optimized process are generation are displayed in Table 7. There are four main sections in Table 7, the first and second sections are the date and time for simulation, and the third section is the actual values of the five design parameters of optimized cases options. The last section is a daylight performance metric.
6.1. Comparison of results
Since UDI is the percentage of time when the illuminance which defined in this study is between 300 lx to 2000 lx. For comparison with the suggested solutions from the optimization algorithm, the simulation results of the base case and the fixed option model are defined firstly. A room without light shelf (BC) is not beneficial to a useful daylight distribution compared to optimized options of light shelf parameters. As well as, it can be reported that the FC option works better than the BC in terms of UDI well-lit, especially in 21 of June and March. It can be noted that most of the space achieve UDI well-lit at least 50% in all different times of testing. The FC option of UDI well-lit value becomes 54.38%, 56.88%, 53.75%, and 50.63% at 21st of June, 54.38%, 51.88%, 55.00% and 53.75% at 21st of March, and 58.75%, 60.63%, 56.25% and 56.88% at 21st of December, which slightly exceeds the minimum target of 50% to achieve of useful UDI well-lit in most times compared to the base case which achieved UDI well-lit by 45.00%, 42.50%, 41.88%, and 42.50% at 21st of June, 45.00%, 39.38%, 41.88% and 41.88% at 21st of March, and 61.25%, 69.39%, 65.63% and 58.13% at 21st of December. Therefore, it can be noted that the UDI over-lit case can be effectively increased in the front areas through the base case model and fixed case option with increased the UDI well-lit, especially with direct sun on December as shown in figures below.
Under the optimized parameters of the light shelf, the inside space of the examination office room has provided more useful illuminance compared to the existing condition of BC and FC, which in turn increased useful UDI. The optimized UDI well-lit value becomes 55.00%, 63.13%, 60.63% and 55.63% at 21st of June, 60.63%, 56.88%, 65.63% and 55.00% at 21st of March, and 63.13%, 78.75%, 73.75% and 61.88% at 21st of December, which exceeds the minimum target of 50% to achieve. Compared to the BC model and FC option, the proposed optimized options show a slight or major increase in the UDI, i.e. between 0.63% and 20.63% at 21st of June, and between 1.25% and 23.75% at 21st of March, and between 1.87% and 18.13% at 21st of December.
Figures 8, 9 and 10 are the comparison of the daylighting performance for BC model, FC option, and the OPTs at four selected times during daily work hours in June, March and December. The orange bar presents the average percentage of the number of nodes (out of 160 nodes) of time that useful UDI is between 300 lx and 2000 lx during work hours (8:00 to 17:00 at least 50%), which is the optimization objective. The grey and blue bars show the percentage of the number of nodes of time un-useful UDI is above 2000 lx and below 100 lx, respectively. After the optimization, compared to the fixed case option, the useful UDI values achieved by optimized options at four tested times; 09:00, 12:00, 15:00 and 17:00 were increased by 0.63%, 6.25%, 6.88%, and 5.00% respectively at 21st of June, and by 6.25%, 5.00%, 10.63%, and 1.25% respectively at 21st of March, and by 4.38%, 18.13%, 17.50%, and 5.00% respectively at 21st of December (December solstice). It can be noted that the UDI over-lit case can be effectively decreased in the front areas through the optimized options of light shelf parameters. After the optimization, most of the time when UDI is above 2000 lx on December solstice with direct sunlight, and a large portion of time when UDI is below 100lx on June solstice and equinox are a significant improvement. The un-useful UDI state can, therefore, be managed efficiently by the method of controlling the optimal light shelf configurations.
6.2. Statistical analysis
In the integrated architectural designs, it will be very advantageous to have the options to identify the most significant design parameters to all the more efficiently develop alternative design proposals or potentially reach optimized design arrangements [82]. Sensitivity and uncertainty analysis are two principle statistical analysis strategies for a superior comprehension of the effects of design parameters along with the design phases and analyze the contribution of each component to the variance of building performance metric [83]. However, the study by Machairas and others [28] mentioned the evaluation of sensitivity and uncertainty to estimate the impact of each design parameter that lead the optimization evaluation to certain directions regarding the collection of design variables and the search algorithms. Instead, the optimization algorithm results may be used to perform statistical analysis. However, for a better understanding of the impacts of design parameters of the light shelf along with the design phases, it is still worthwhile to perform a sensitivity analysis or uncertainty analysis and investigate the contribution of each variable standalone.
Since there are limited design parameters in this study (only Five parameters), the analysis is directly performed with the optimized options without the simplification of design parameters the study focused on. Thus, the present study applied a statistical analysis using linear regression analysis (R2) method to determine the relationship between input parameters of optimal cases and daylight performance, which is the most widely used method to assess the relationship between prediction results from the GA process through a simplified comparison of the UDI (300-2000 lx) results; these values were further tested through regression and correlation analyses to increase the validity of optimization results performance from GA. In addition to R2 the mean values (M), standard deviations (Std), and variation coefficients (V) were calculated using Excel Data Analysis and formulas. The UDI of BC and FC was taken as reference data while the 12 OPTs cases as test data.
Based on the five selected design parameters which generated 12 optimal options of light shelf configuration. As shown in Table 8, the analysis indicated a significant correlation between the BC, FC, and OPTs of the UDI results. The outcomes showed that the R2 ranged from 0.96 to 0.99 on the 21st of June, and from 0.95 to 0.97 at 21st of March, and from 0.39 to 0.98 at 21st of December which indicated a high level of reliability. The results justified that the GA based on Radiance-based simulation software was able to accurately predict of optimized solutions between many configurations of light-shelf parameters.
Table 8
Table 8. R2, Mean, standard deviation, and coefficient of variation to validate the UDI results from GA.
Besides R2, the coefficient of variation was calculated as shown in Table 7, the results showed that the OPT10 and OPT11 have the highest coefficient of variation up to over 50%, followed by OPT2, OPT7 and OPT12 up to over 40%, for the other cases of OPTs, the coefficient of variation is less than (40%). The high values of the variation coefficient underline large output dispersions, showing that decisions should be taken at the design stage very carefully to ensure the different building performance indicators remain in the preferred range. The large dispersion of some cases evaluated of OPTs parameters calls for further analysis to identify the most influential factors. Due to the different OPTs for different dates and times show the different coefficient of variation characteristics, the uncertainty, and sensitivity analysis needs to be performed for all tested parameters.
7. Conclusion
An optimization to determine the most appropriate light shelf parameters for the case of daylight optimization in a reference office space has been conducted, using a GA. An investigation study to determine the most appropriate light shelf parameters for the case of daylight performance enhancement using useful daylight illuminance indicator, in a reference office space with fully glazing south-facing has conducted, by comparing various light shelf configurations through a parametric simulation study, using integrated parametric Rhino/Grasshopper plug-ins with Radiance. To evaluate the suitability of the various configurations of light shelf for use in fully glazing facade design, a criterion UDI 300-2000lx thresholds relating to the effectiveness of the daylit office environment was established. This paper presents a parametric method that couples a parametric modelling tools with Radiance daylight simulation engine and applies it to select optimal values of light shelf design parameters associated with fully glazing facade office buildings in the climate of the tropics of Malaysia to maximizing useful daylight through working hours.
During June solstice (21st of June) and equinox (21st of March) with diffused sunlight, most of the of space was located in the UDI under-lit or over-lit set, it was exceeding the half of the space at different times with max value by 58.1% and 60.6% respectively, while at the December solstice with direct sunlight the over-lit values were reached up to 30% for BC, while the OPTs are work to manage the illuminance performance by maximized the useful UDI (well-lit 300lx-2000lx) value through decreased the un-useful UDI values (under-lit and over-lit). Figures showed the comparison of the daylighting performance of BC, FC, and the daylight performance by different OPTs on different solstices. The figures showed that the largest daylighting performance improvement is found in OPTs compared to other two cases, and the majority of the time when UDI is above 2000 lx on winter solstice with direct sunlight, and a large portion of time when UDI is below 100lx on June solstice and equinox are significantly decreased or eliminated in some cases.
The optimization results of the simulations focused on the illuminance performance for horizontal work-plane. The comparisons of illuminance levels were conducted among the optimal parameters of the light shelf. The comparison of the results of optimal design options (OPTs) with references models (BC and FC) clearly showed great potential in raising the useful daylight levels in all hours. In terms of the overall OPTs for the UDI Over-lit areas and UDI under-lit areas, were reduced or increased by -10.0% and 1.3% respectively compared with the BC, and by -5.0% and 0.0% respectively compared with the FC at June solstice, and by -14.4% and 0.6% respectively compared with the BC, and it gives the same results compared with the FC at equinox, and by -3.1% and 14.4% respectively compared with the BC, and by -16.9% and 3.4% respectively compared with the FC at December solstice. While the average UDI well-lit (300–2000 lx) from OPTs yields an increase of 13.8%, 13.8%, and 5.6%, and by 5.0%, 0.0% and 13.1% at June solstice, equinox and December solstice respectively compared to references models (BC and FC). This results compared well to the other studies, for example; a study by Mangkuto et al. [2], the results of the optimised values of the light shelf were obtained for the east and west façades. The results by optimised values yielded an increase UDI of 4.9% and by 16.7% compared to the existing condition of a case study.
Statistical analysis is performed to analyze the relationship between OPTs and performance metrics (UDI) compared to BC and FC. The results reveal that the outcomes showed that the regression analysis (R2) indicated a high level of reliability. The results justified that the GA based on Radiance-based simulation software was able to accurately predict of optimized solutions between many different configurations of light shelf parameters. OPTs showed different levels of coefficient of variation and even opposite influence on daylight performance for different tested solstice and times. The large dispersion of some cases evaluated of OPTs parameters calls for further analysis to identify the most influential factors. Because the different OPTs for different dates and times show the different coefficient of variation characteristics, the uncertainty, and sensitivity analysis needs to be performed for all tested parameters.
Future work may include the application of this optimization process on different daylight aspects such as thermal comfort, visual comfort (glare probability), and energy-saving. Future work may also include the application of this optimization process on more complex design light shelf parameters and uncertainty and sensitivity analysis could be performed before the optimization to simplify the design problem of light-shelf parameters and to identify the key design of most design parameters of light-shelf that influence each performance daylight indices and then summarized as design guidelines.
Contributions
All authors contributed equally in the preparation of this article.
Declaration of competing interest
The authors report no conflicts of interest. The authors alone are responsible for the content and writing of this article.
References
- A. Zhang, R. Bokel, A. van den Dobbelsteen, Y. Sun, Q. Huang, Q. Zhang, Optimization of thermal and daylight performance of school buildings based on a multi-objective genetic algorithm in the cold climate of China, Energy and Buildings 139 (2017) 371-384. https://doi.org/10.1016/j.enbuild.2017.01.048
- R.A. Mangkuto, F. Feradi, R.E. Putra, R.T. Atmodipoero, F. Favero, Optimisation of daylight admission based on modifications of light shelf design parameters, Journal of Building Engineering 18 (2018) 195-209. https://doi.org/10.1016/j.jobe.2018.03.007
- A. Meresi, Evaluating daylight performance of light shelves combined with external blinds in south-facing classrooms in Athens, Greece, Energy and Buildings 116 (2016) 190-205. https://doi.org/10.1016/j.enbuild.2016.01.009
- N. Nasrollahi, E. Shokry, Parametric Analysis of Architectural Elements on Daylight, Visual Comfort, and Electrical Energy Performance in the Study Spaces, Journal of Daylighting 7 (2020) 57-72. https://doi.org/10.15627/jd.2020.5
- M.N. Majeed, F.A. Mustafa, H.A. Husein, Impact of Building Typology on Daylight Optimization Using Building Information Modeling: Apartments in Erbil City as a Case Study, Journal of Daylighting 6 (2019) 187-201. https://doi.org/10.15627/jd.2019.17
- H.H. Alzoubi, A.H. Al-Zoubi, Assessment of building façade performance in terms of daylighting and the associated energy consumption in architectural spaces: Vertical and horizontal shading devices for southern exposure facades, Energy Conversion and Management 51 (2010) 1592-1599. https://doi.org/10.1016/j.enconman.2009.08.039
- A. Kontadakis, A. Tsangrassoulis, L. Doulos, F. Topalis, An active sunlight redirection system for daylight enhancement beyond the perimeter zone, Building and Environment 113 (2017) 267-279. https://doi.org/10.1016/j.buildenv.2016.09.029
- Y.W. Lim, M.H. Ahmad, The effects of direct sunlight on light shelf performance under tropical sky, Indoor and Built Environment 24 (2015) 788-802. https://doi.org/10.1177/1420326x14536066
- R.A. Mangkuto, M.A.A. Siregar, A. Handina, Determination of appropriate metrics for indicating indoor daylight availability and lighting energy demand using genetic algorithm, Solar Energy 170 (2018) 1074-1086. https://doi.org/10.1016/j.solener.2018.06.025
- E. Assem, A. Al-Mumin, Code compliance of fully glazed tall office buildings in hot climate, Energy and buildings 42 7 (2010) 1100-1105. https://doi.org/10.1016/j.enbuild.2010.02.001
- A. Kontadakis, A. Tsangrassoulis, A. Roetzel, Defining the Boundaries of Daylight Penetration. The use of dynamic and static daylight methods to predict the daylit zone within sidelit spaces, a comparison, in: Proceedings of the 2015 Balkan Light Conference, 2015, pp. 97-102, Athens, Greece.
- C.F. Reinhart, A simulation-based review of the ubiquitous window-head-height to daylit zone depth rule-of-thumb, in: Building Simulation, 2005, pp. 1011-1018, Montréal, Canada.
- J. Cho, C. Yoo, Y. Kim, Viability of exterior shading devices for high-rise residential buildings: Case study for cooling energy saving and economic feasibility analysis, Energy and Buildings 82 (2014) 771-785. https://doi.org/10.1016/j.enbuild.2014.07.092
- T. Du, S. Jansen, M. Turrin, A. van den Dobbelsteen, Impact of space layout on energy performance of office buildings coupling daylight with thermal simulation, in: E3S Web of Conferences, 2019. https://doi.org/10.1051/e3sconf/201911103077
- H.M.T. El Daly, Automated fenestration allocation as complying with LEED rating system, Alexandria Engineering Journal 53 4 (2014) 883-890. https://doi.org/10.1016/j.aej.2014.09.011
- M. Konstantoglou, A. Tsangrassoulis, Dynamic operation of daylighting and shading systems: A literature review, Renewable and Sustainable Energy Reviews 60 (2016) 268-283. https://doi.org/10.1016/j.rser.2015.12.246
- I. Ullah, Heliostats Daylighting System for Multi-floor Buildings, Journal of Daylighting 6 (2019) 202-209. https://doi.org/10.15627/jd.2019.18
- M. Alrubaih, M.F.M. Zain, M. Alghoul, N.L.N. Ibrahim, M. Shameri, O. Elayeb, Research and development on aspects of daylighting fundamentals, Renewable and Sustainable Energy Reviews 21 (2013) 494-505. https://doi.org/10.1016/j.rser.2012.12.057
- P. Zazzini, A. Romano, A. Di Lorenzo, V. Portaluri, A. Di Crescenzo, Experimental Analysis of the Performance of Light Shelves in Different Geometrical Configurations Through the Scale Model Approach, Journal of Daylighting 7 (2020) 37-56. https://doi.org/10.15627/jd.2020.4
- A. Eltaweel, Y. Su, Controlling venetian blinds based on parametric design; via implementing Grasshopper’s plugins: A case study of an office building in Cairo, Energy and Buildings 139 (2017) 31-43. https://doi.org/10.1016/j.enbuild.2016.12.075
- M. Ayoub, Integrating illuminance and energy evaluations of cellular automata controlled dynamic shading system using new hourly-based metrics, Solar Energy 170 (2018) 336-351. https://doi.org/10.1016/j.solener.2018.05.041
- A. Chronis, K.A. Liapi, I. Sibetheros, A parametric approach to the bioclimatic design of large scale projects: The case of a student housing complex, Automation in construction 22 (2012) 24-35. https://doi.org/10.1016/j.autcon.2011.09.007
- S. Attia, J.L. Hensen, L. Beltrán, A. De Herde, Selection criteria for building performance simulation tools: contrasting architects' and engineers' needs, Journal of Building Performance Simulation 5 (2012) 155-169. https://doi.org/10.1080/19401493.2010.549573
- Y.-W. Lim, C. Heng, Dynamic internal light shelf for tropical daylighting in high-rise office buildings, Building and Environment 106 (2016) 155-166. https://doi.org/10.1016/j.buildenv.2016.06.030
- R. Wang, S. Lu, W. Feng, Impact of adjustment strategies on building design process in different climates oriented by multiple performance, Applied Energy 266 (2020) 114822. https://doi.org/10.1016/j.apenergy.2020.114822
- M.R. Asl, S. Zarrinmehr, M. Bergin, W. Yan, BPOpt: A framework for BIM-based performance optimization, Energy and Buildings 108 (2015) 401-412. https://doi.org/10.1016/j.enbuild.2015.09.011
- R. Vierlinger, K. Bollinger, Accommodating change in parametric design, in: Proceedings of ACADIA, 2014, pp. 609-618, Los Angeles.
- V. Machairas, A. Tsangrassoulis, K. Axarli, Algorithms for optimization of building design: A review, Renewable and sustainable energy reviews 31 (2014) 101-112. https://doi.org/10.1016/j.rser.2013.11.036
- S. Subramaniam, Daylighting Simulations with Radiance using Matrix-based Methods, Lawrence Berke-ley National Laboratory, 2017.
- H. Djamila, C.C. Ming, S. Kumaresan, Estimation of exterior vertical daylight for the humid tropic of Kota Kinabalu city in East Malaysia, Renewable energy 36 (2011) 9-15. https://doi.org/10.1016/j.renene.2010.06.040
- M. Roshan, A.S. Barau, Assessing Anidolic Daylighting System for efficient daylight in open plan office in the tropics, Journal of Building Engineering 8 (2016) 58-69. https://doi.org/10.1016/j.jobe.2016.07.002
- A. Zain-Ahmed, K. Sopian, Z.Z. Abidin, M. Othman, The availability of daylight from tropical skies—a case study of Malaysia, Renewable Energy 25 (2002) 21-30. https://doi.org/10.1016/s0960-1481(00)00209-3
- K.M. Al-Obaidi, M.A.C. Munaaim, M.A. Ismail, A.M.A. Rahman, Designing an integrated daylighting system for deep-plan spaces in Malaysian low-rise buildings, Solar Energy 149 (2017) 85-101. https://doi.org/10.1016/j.solener.2017.04.001
- C.-S. Kim, S.-J. Chung, Daylighting simulation as an architectural design process in museums installed with toplights, Building and Environment 46 1 (2011) 210-222. https://doi.org/10.1016/j.buildenv.2010.07.015
- G.-H. Lim, M.B. Hirning, N. Keumala, N.A. Ghafar, Daylight performance and users’ visual appraisal for green building offices in Malaysia, Energy and Buildings 141 (2017) 175-185. https://doi.org/10.1016/j.enbuild.2017.02.028
- G. Ramos, E. Ghisi, Analysis of daylight calculated using the EnergyPlus programme, Renewable and Sustainable Energy Reviews 14 (2010) 1948-1958. https://doi.org/10.1016/j.rser.2010.03.040
- C.F. Reinhart, M. Andersen, Development and validation of a Radiance model for a translucent panel, Energy and Buildings 38 (2006) 890-904. https://doi.org/10.1016/j.enbuild.2006.03.006
- A. Nabil, J. Mardaljevic, Useful daylight illuminances: A replacement for daylight factors, Energy and buildings 38 (2006) 905-913. https://doi.org/10.1016/j.enbuild.2006.03.013
- F. Cantin, M.-C. Dubois, Daylighting metrics based on illuminance, distribution, glare and directivity, Lighting Research & Technology 43 (2011) 291-307. https://doi.org/10.1177/1477153510393319
- S. Carlucci, G. Cattarin, F. Causone, L. Pagliano, Multi-objective optimization of a nearly zero-energy building based on thermal and visual discomfort minimization using a non-dominated sorting genetic algorithm (NSGA-II), Energy and Buildings 104 (2015) 378-394. https://doi.org/10.1016/j.enbuild.2015.06.064
- J. Mardaljevic, L. Heschong, E. Lee, Daylight metrics and energy savings, Lighting Research & Technology 41 (2009) 261-283. https://doi.org/10.1177/1477153509339703
- C.F. Reinhart, Effects of interior design on the daylight availability in open plan offices, Proceedings of the 2002 American Council for an Energy Efficient Economy (ACEEE) Summer Study on Energy Efficiency in Buildings 3 (2002) 309-322.
- C.F. Reinhart, J. Wienold, The daylighting dashboard–A simulation-based design analysis for daylit spaces, Building and environment 46 (2011) 386-396. https://doi.org/10.1016/j.buildenv.2010.08.001
- D.A. Chi, D. Moreno, J. Navarro, Design optimisation of perforated solar façades in order to balance daylighting with thermal performance, Building and Environment 125 (2017) 383-400. https://doi.org/10.1016/j.buildenv.2017.09.007
- R. Saraiji, M.Y. Al Safadi, N. Al Ghaithi, R.G. Mistrick, A comparison of scale-model photometry and computer simulation in day-lit spaces using a normalized daylight performance index, Energy and Buildings 89 (2015) 76-86. https://doi.org/10.1016/j.enbuild.2014.12.033
- I. Acosta, M.Á. Campano, J.F. Molina, Window design in architecture: Analysis of energy savings for lighting and visual comfort in residential spaces, Applied energy 168 (2016) 493-506. https://doi.org/10.1016/j.apenergy.2016.02.005
- S. Motamedi, P. Liedl, Integrative algorithm to optimize skylights considering fully impacts of daylight on energy, Energy and Buildings 138 (2017) 655-665. https://doi.org/10.1016/j.enbuild.2016.12.045
- C.F. Reinhart, D.A. Weissman, The daylit area–Correlating architectural student assessments with current and emerging daylight availability metrics, Building and environment 50 (2012) 155-164. https://doi.org/10.1016/j.buildenv.2011.10.024
- X. Yu, Y. Su, Daylight availability assessment and its potential energy saving estimation–A literature review, Renewable and Sustainable Energy Reviews 52 (2015) 494-503. https://doi.org/10.1016/j.rser.2015.07.142
- D. A. C. Pool, A Comprehensive Evaluation of Perforated Façades for Daylighting and Solar Shading Performance: Effects of Matrix, Thickness and Separation Distance, Journal of Daylighting 6 (2019) 97-111. https://doi.org/10.15627/jd.2019.10
- M. Standard, SM 1525, Energy efficiency and use of renewable energy for non-residential buildings–Code of practice (Second revision), Department of Standards Malaysia, 2014.
- Z. JIS, General rules of recommended lighting levels, Japanese Industrial, Standards Committee, Tokyo, Japan, 2010.
- K.S. Association, KS A 3011 Recommended levels of illumination, Korean Standards Association, 1998.
- ladybug, tools, Accessed on: 2019, Available at: https://www.ladybug.tools/epwmap/.
- A. Zain-Ahmed, K. Sopian, M. Othman, A. Sayigh, P. Surendran, Daylighting as a passive solar design strategy in tropical buildings: a case study of Malaysia, Energy conversion and management 43 (2002) 1725-1736. https://doi.org/10.1016/s0196-8904(01)00007-3
- JALOXA, Radiance Colour Picker, Accessed on: 2019, Available At: http://www.jaloxa.eu/resources/radiance/colour_picker/index.shtml.
- Y.-W. Lim, M.H. Ahmad, D.R. Ossen, Empirical validation of daylight simulation tool with physical model measurement, American Journal of Applied Sciences 7 10 (2010) 1426.
- Y.-W. Lim, M.Z. Kandar, M.H. Ahmad, D.R. Ossen, A.M. Abdullah, Building façade design for daylighting quality in typical government office building, Building and Environment 57 (2012) 194-204. https://doi.org/10.1016/j.buildenv.2012.04.015
- N.D. Dahlan, P.J. Jones, D.K. Alexander, E. Salleh, J. Alias, Daylight ratio, luminance, and visual comfort assessments in typical Malaysian hostels, Indoor and Built Environment 18 (2009) 319-335. https://doi.org/10.1177/1420326x09337041
- D. Li, E. Tsang, I. Edmonds, Performance of light redirection systems in model buildings under typical sky and building obstruction conditions encountered in Hong Kong, Indoor and Built Environment 20 (2011) 638-648. https://doi.org/10.1177/1420326x11409456
- D. Ibarra, C.F. Reinhart, Daylight factor simulations–how close do simulation beginners ‘really’get, in: Building simulation, 2009, pp. 203, Glasgow, Scotland.
- Y.-W. Lim, M.H. Ahmad, D.R. Ossen, Internal shading for efficient tropical daylighting in Malaysian contemporary high-rise open plan office, Indoor and Built Environment 22 (2013) 932-951. https://doi.org/10.1177/1420326x12463024
- H.L. Chang, Evaluation and Development of Solar Control Screens: Using Daylight Simulation to Improve The Performance of Facade Solar Control Screens, University of Southern California, 2015.
- S. Mirrahimi, M.F. Mohamed, L.C. Haw, N.L.N. Ibrahim, W.F.M. Yusoff, A. Aflaki, The effect of building envelope on the thermal comfort and energy saving for high-rise buildings in hot–humid climate, Renewable and Sustainable Energy Reviews 53 (2016) 1508-1519. https://doi.org/10.1016/j.rser.2015.09.055
- S. Lee, K.S. Lee, A Study on the Improvement of the Evaluation Scale of Discomfort Glare in Educational Facilities, Energies 12 (2019) 3265. https://doi.org/10.3390/en12173265
- A. Tabadkani, S. Banihashemi, M.R. Hosseini, Daylighting and visual comfort of oriental sun responsive skins: A parametric analysis, Building simulation 11 (2018) 663-676. https://doi.org/10.1007/s12273-018-0433-0
- S. Crone, Radiance Users Manual, Architectural Dissertation, 1992.
- D. Moult, Radiance specularity and roughness value examples, Accessed on: 2019, Available At: https://thinkmoult.com/radiance-specularity-and-roughness-value-examples.html.
- N. Baker, Modelling and Analysis of Daylight, Solar Heat Gains and Thermal Losses to Inform the Early Stage of the Architectural Process, 2017.
- R.A. Mangkuto, D.K. Dewi, A.A. Herwandani, M.D. Koerniawan, Design optimisation of internal shading device in multiple scenarios: Case study in Bandung, Indonesia, Journal of Building Engineering 24 (2019) 100745. https://doi.org/10.1016/j.jobe.2019.100745
- M. Joarder, A. Rahman, Z.N. Ahmed, A. Price, M. Mourshed, A simulation assessment of the height of light shelves to enhance daylighting quality in tropical office buildings under overcast sky conditions in Dhaka, Bangladesh, in: Building Simulation, 2009, pp. 1706-1713, Glasgow, Scotland.
- M.H. Moazzeni, Z. Ghiabaklou, Investigating the influence of light shelf geometry parameters on daylight performance and visual comfort, a case study of educational space in Tehran, Iran, Buildings 6 (2016) 26. https://doi.org/10.3390/buildings6030026
- C.F. Reinhart, O. Walkenhorst, Validation of dynamic RADIANCE-based daylight simulations for a test office with external blinds, Energy and buildings 33 (2001) 683-697. https://doi.org/10.1016/s0378-7788(01)00058-5
- L. Bellia, F. Fragliasso, New parameters to evaluate the capability of a daylight-linked control system in complementing daylight, Building and Environment 123 (2017) 223-242. https://doi.org/10.1016/j.buildenv.2017.07.001
- U. Berardi, H.K. Anaraki, Analysis of the impacts of light shelves on the useful daylight illuminance in office buildings in Toronto, Energy Procedia 78 (2015) 1793-1798. https://doi.org/10.1016/j.egypro.2015.11.310
- A. Eltaweel, S. Yuehong, Using integrated parametric control to achieve better daylighting uniformity in an office room: A multi-Step comparison study, Energy and Buildings 152 (2017) 137-148. https://doi.org/10.1016/j.enbuild.2017.07.033
- Y. Shahbazi, M. Heydari, F. Haghparast, An early-stage design optimization for office buildings’ façade providing high-energy performance and daylight, Indoor and Built Environment 28 (2019) 1350-1367. https://doi.org/10.1177/1420326x19840761
- Y. Sun, D. Liu, J.-F. Flor, K. Shank, H. Baig, R. Wilson, H. Liu, S. Sundaram, T.K. Mallick, Y. Wu, Analysis of the daylight performance of window integrated photovoltaics systems, Renewable Energy 145 (2020) 153-163. https://doi.org/10.1016/j.renene.2019.05.061
- Y.K. Yi, J. Yin, Y. Tang, Developing an advanced daylight model for building energy tool to simulate dynamic shading device, Solar Energy 163 (2018) 140-149. https://doi.org/10.1016/j.solener.2018.01.082
- H. Lee, Performance evaluation of a light shelf with a solar module based on the solar module attachment area, Building and Environment 159 (2019) 106-161. https://doi.org/10.1016/j.buildenv.2019.106161
- P.J. Littlefair, Light shelves: computer assessment of daylighting performance, International Journal of Lighting Research and Technology 27 (1995) 79-91. https://doi.org/10.1177/14771535950270020201
- P. Heiselberg, H. Brohus, A. Hesselholt, H. Rasmussen, E. Seinre, S. Thomas, Application of sensitivity analysis in design of sustainable buildings, Renewable Energy 34 (2009) 2030-2036. https://doi.org/10.1016/j.renene.2009.02.016
- Y. Fang, S. Cho, Design optimization of building geometry and fenestration for daylighting and energy performance, Solar Energy 191 (2019) 7-18. https://doi.org/10.1016/j.solener.2019.08.039
Copyright © 2020 The Author(s). Published by solarlits.com.
 HOME
HOME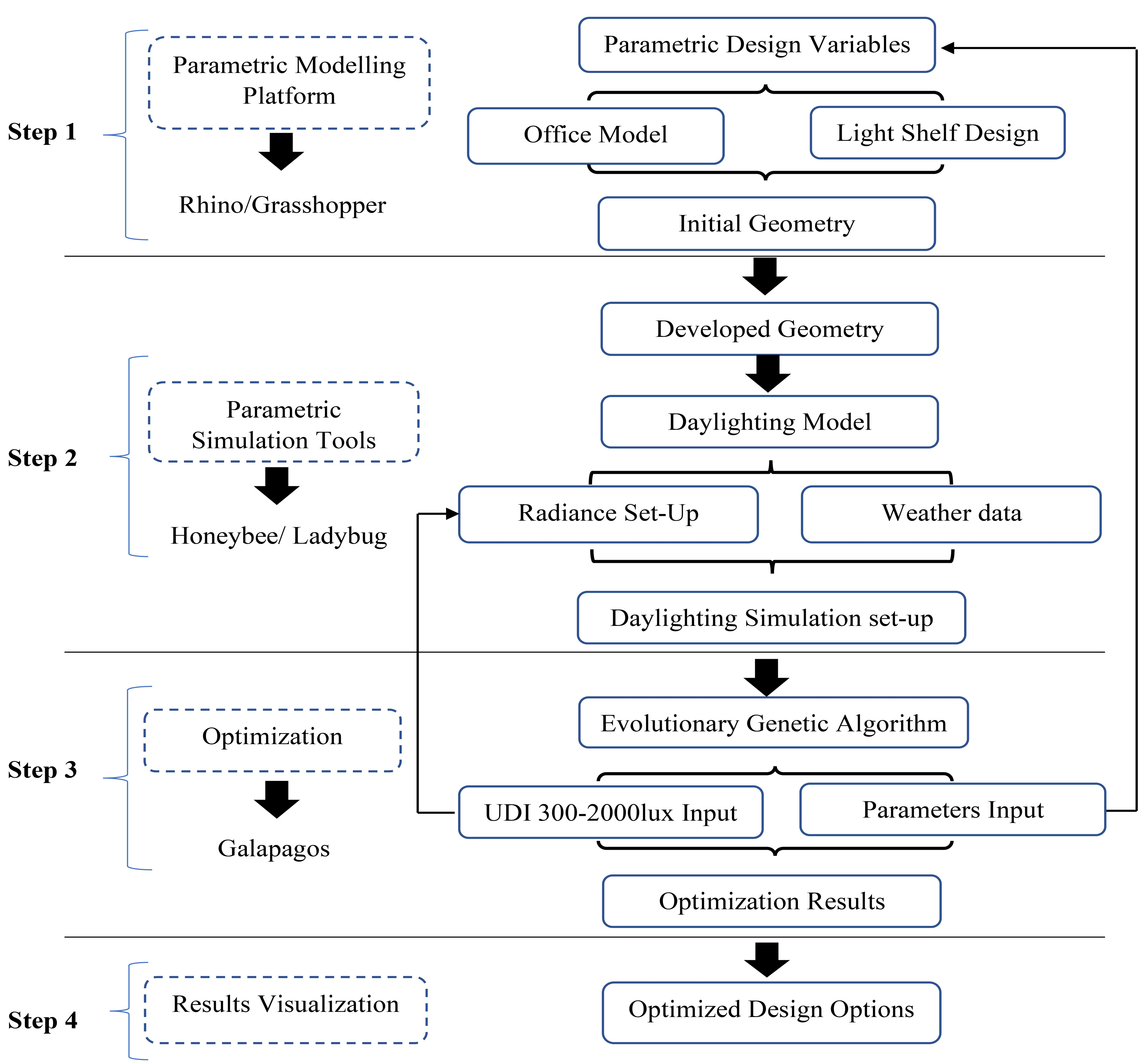 Figure 1
Figure 1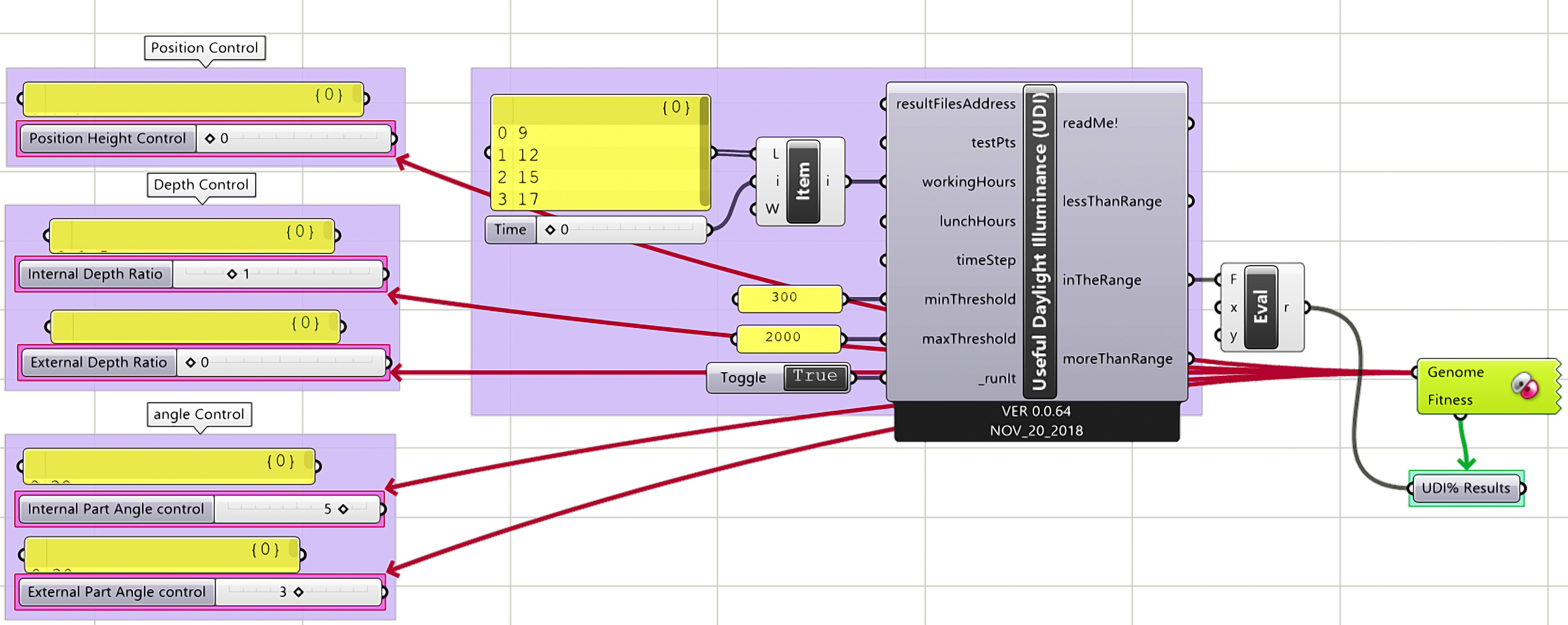 Figure 2
Figure 2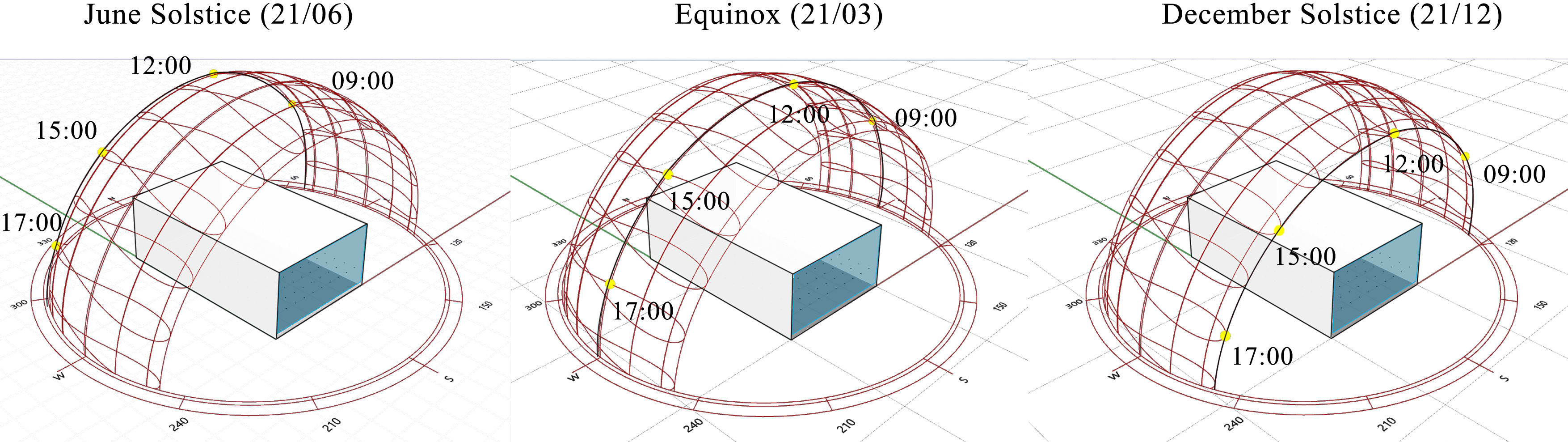 Figure 3
Figure 3 Table 1
Table 1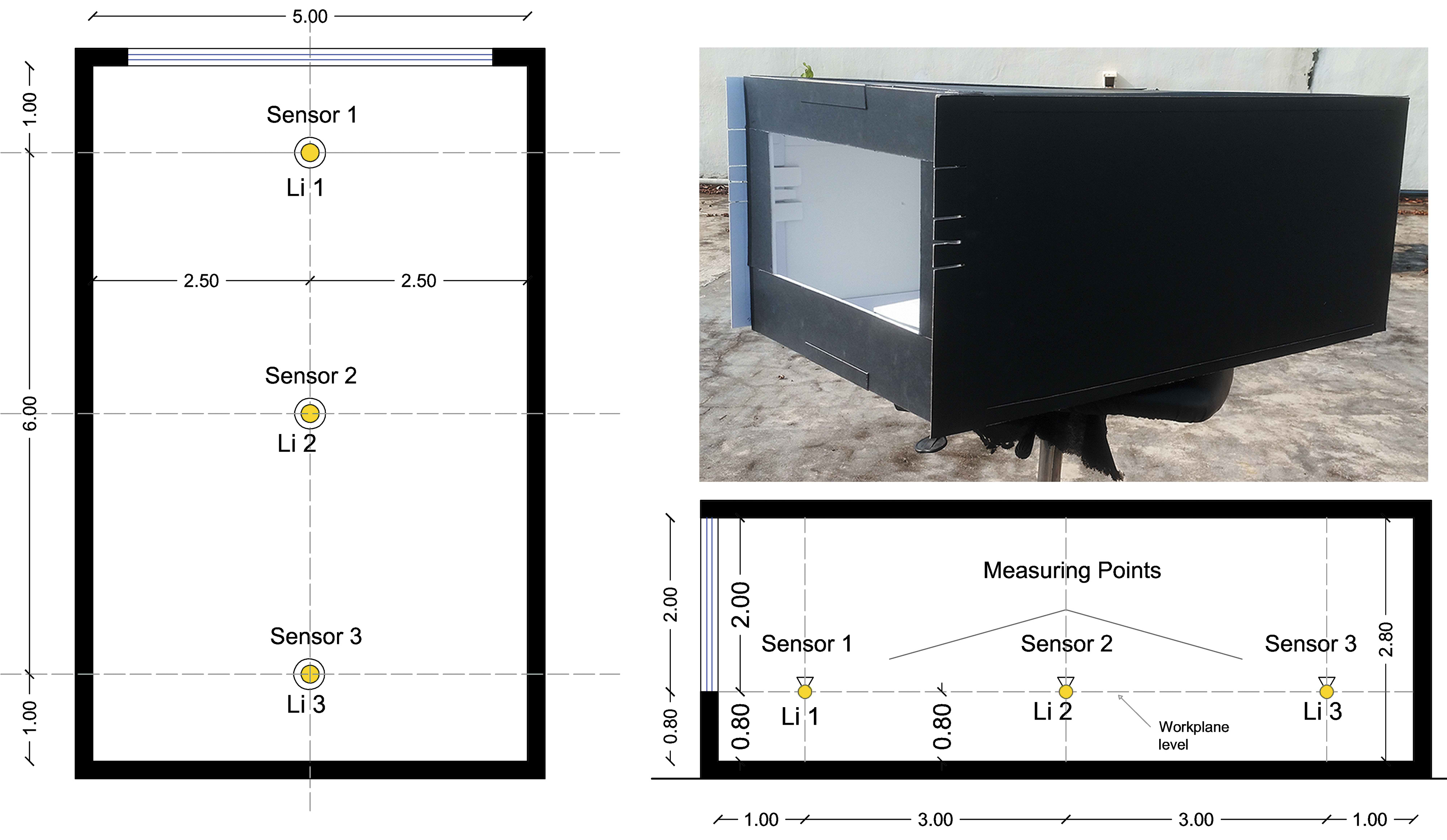 Figure 4
Figure 4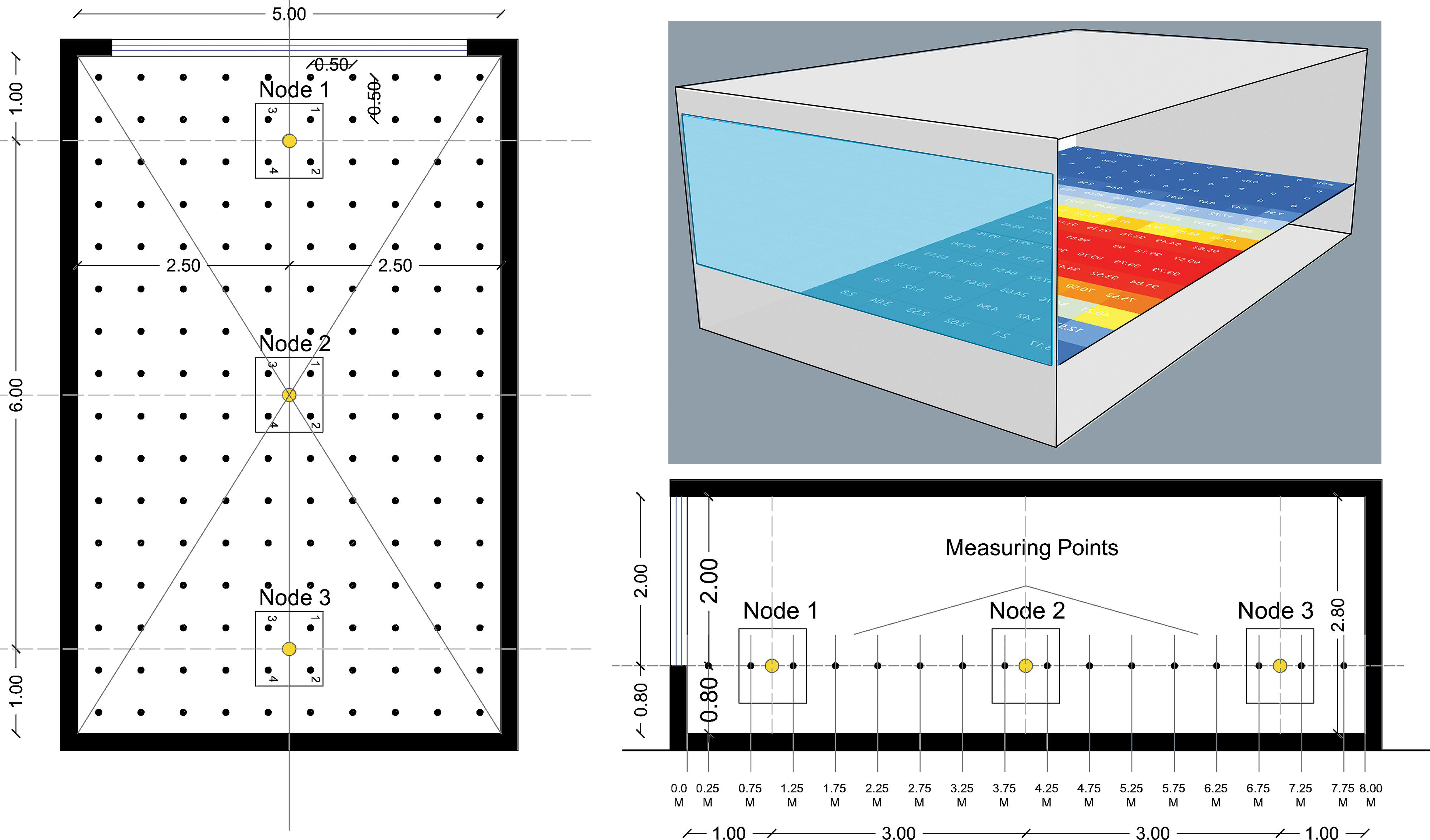 Figure 5
Figure 5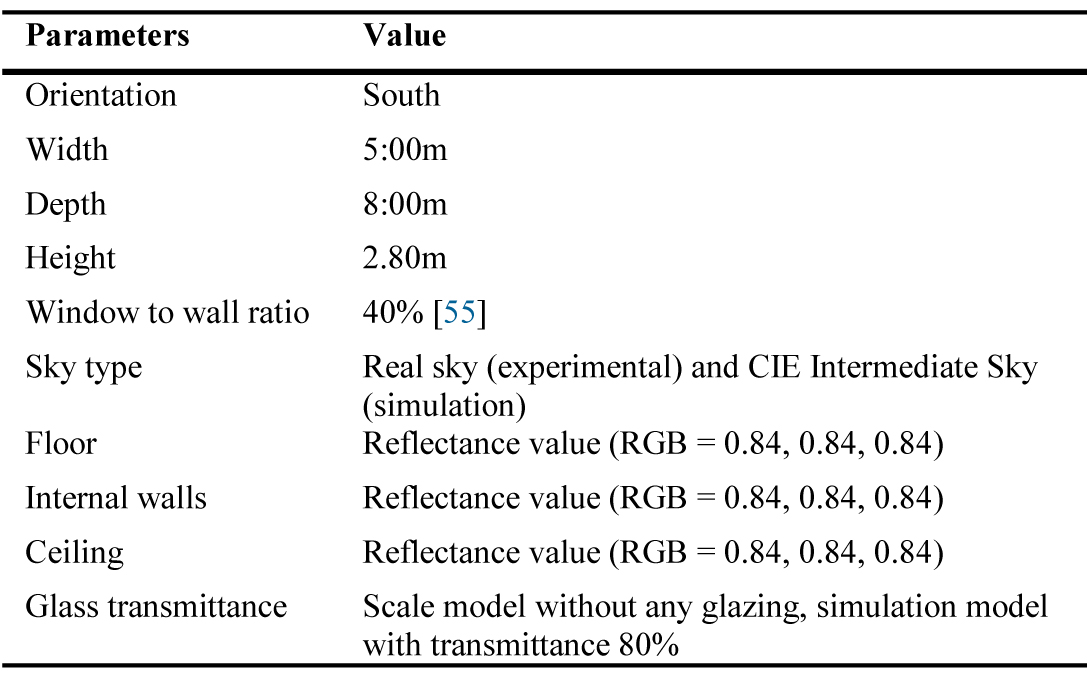 Table 2
Table 2 Table 3
Table 3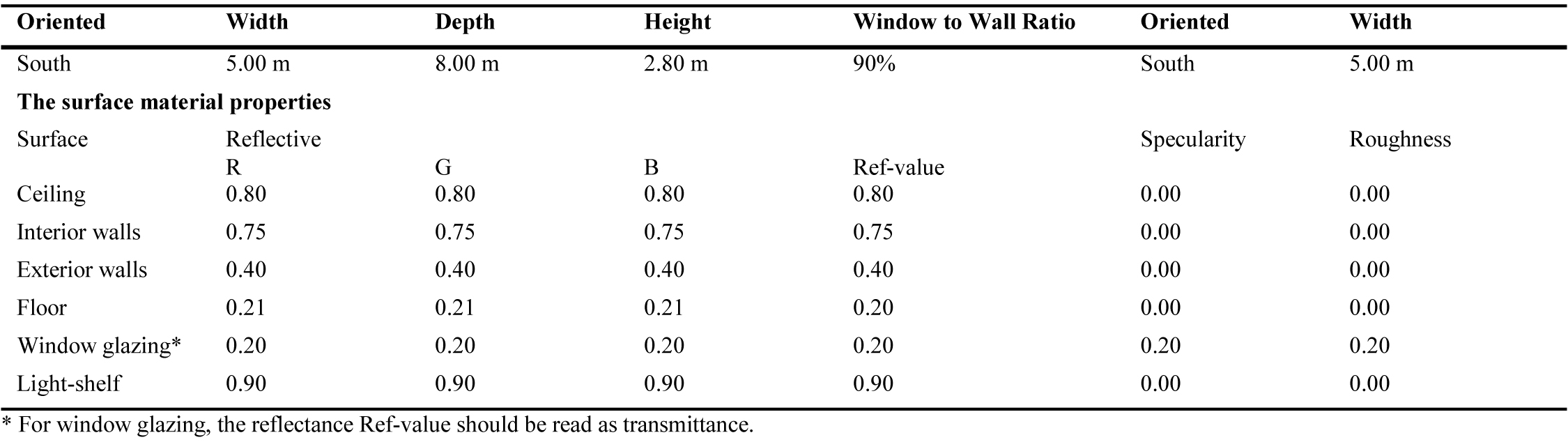 Table 4
Table 4 Table 5
Table 5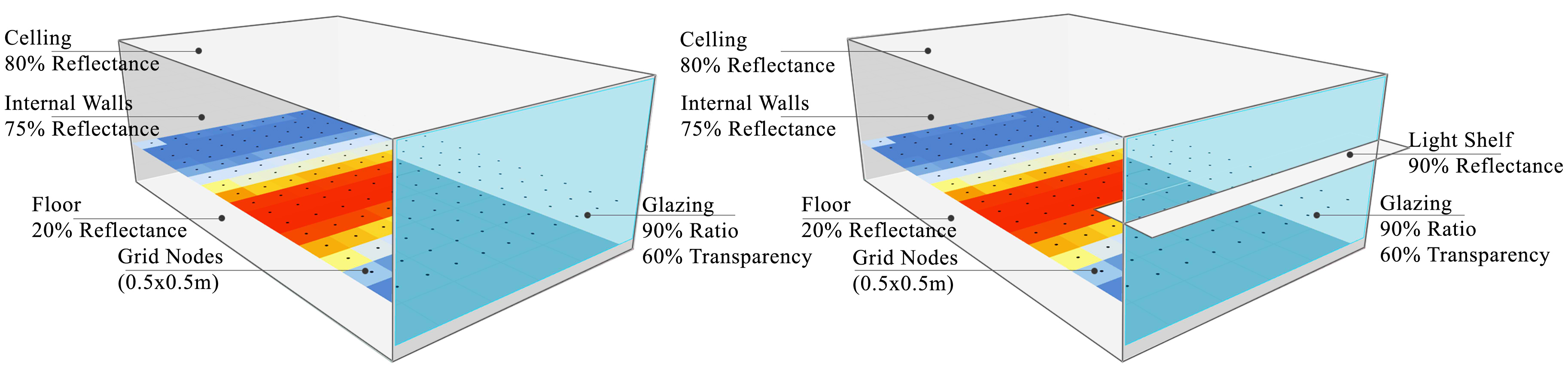 Figure 6
Figure 6 Table 6
Table 6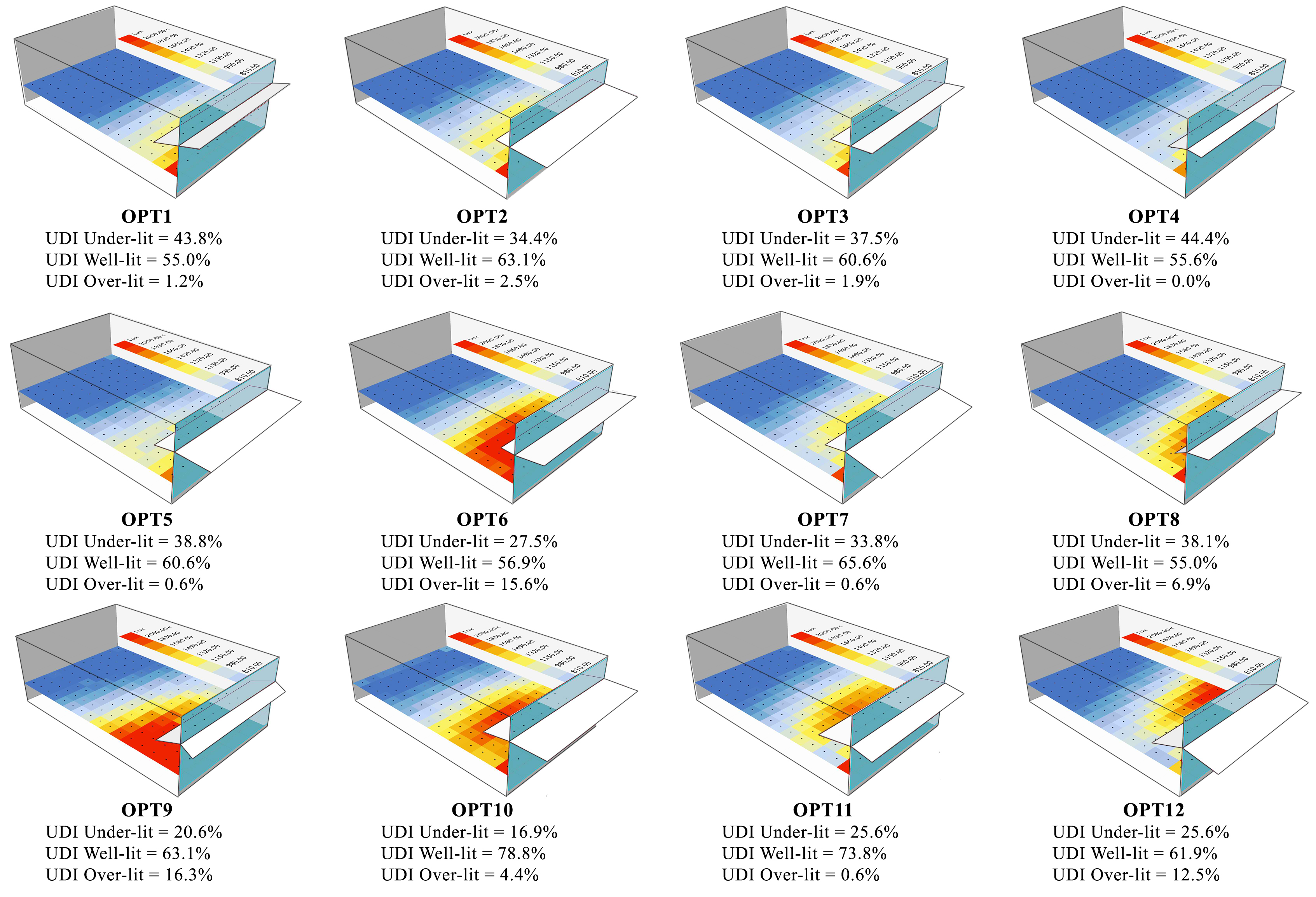 Figure 7
Figure 7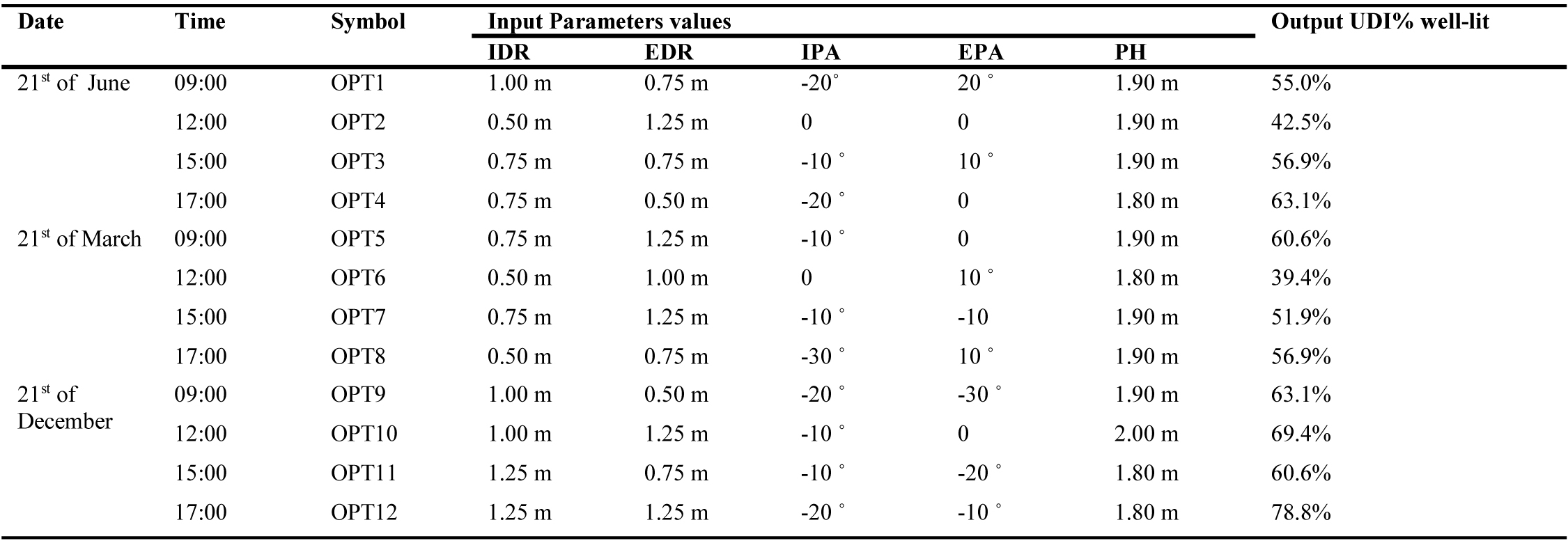 Table 7
Table 7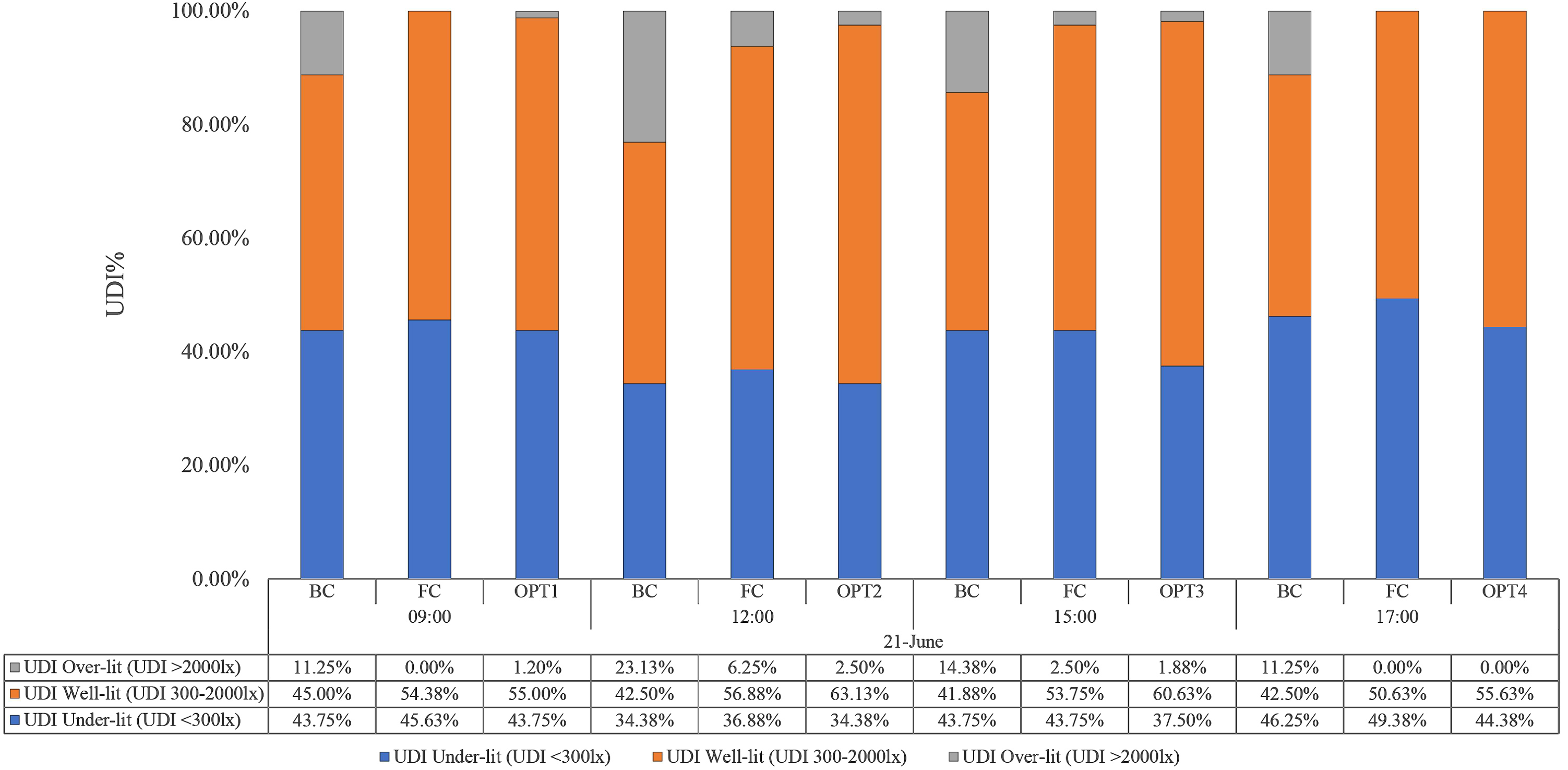 Figure 8
Figure 8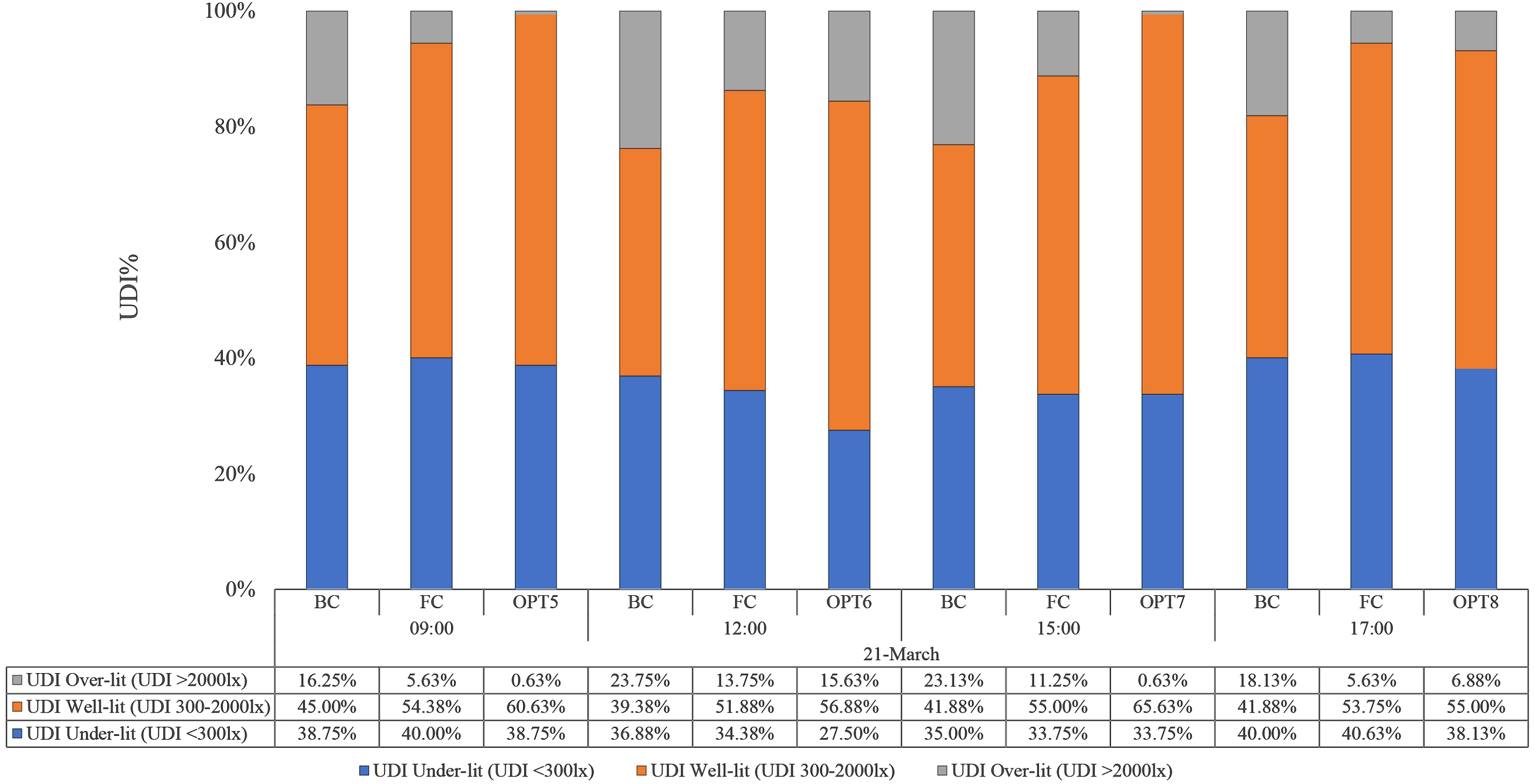 Figure 9
Figure 9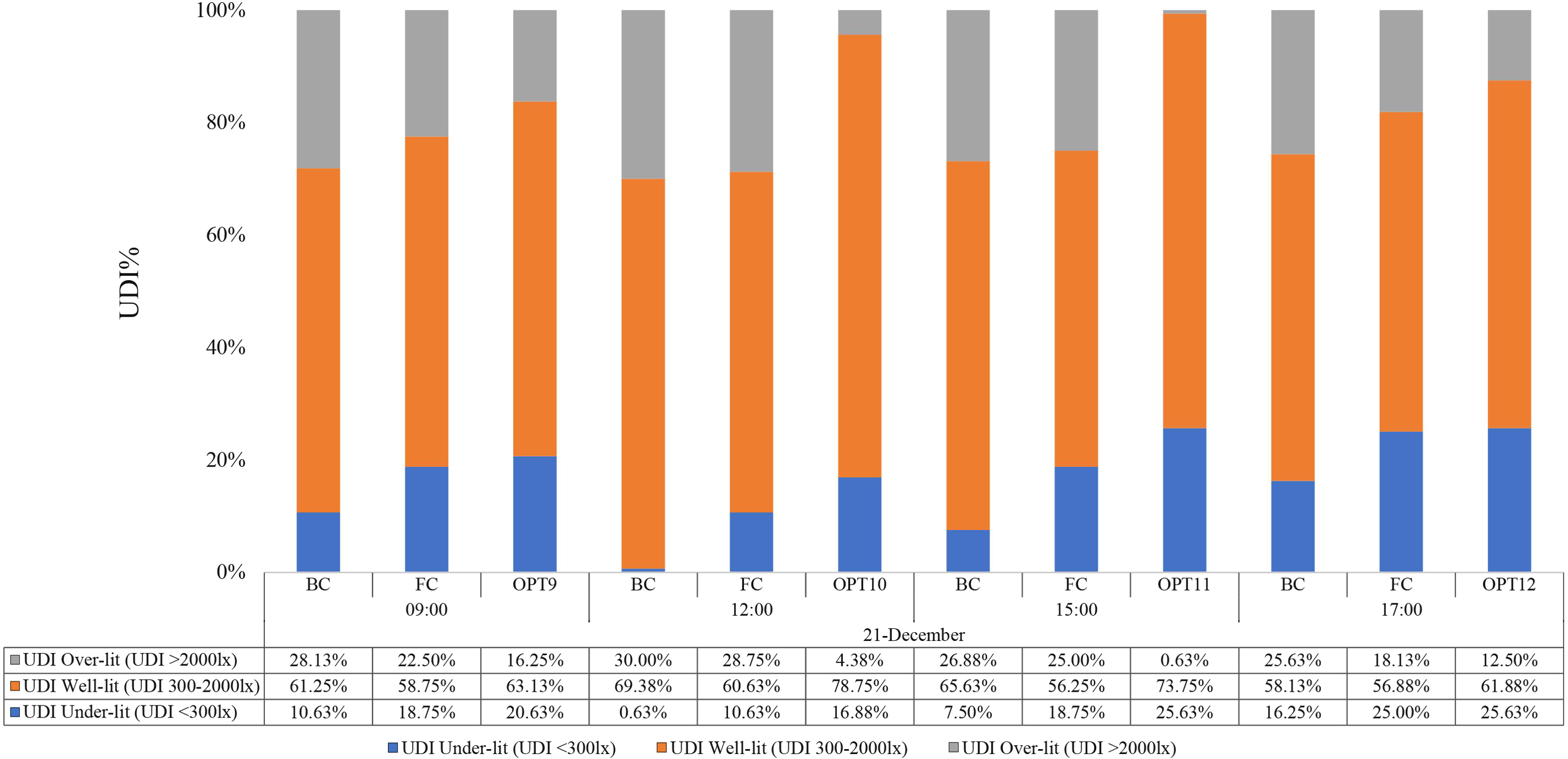 Figure 10
Figure 10 Table 8
Table 8


