Volume 7 Issue 2 pp. 238-245 • doi: 10.15627/jd.2020.20
Improvement of Optical Performances Using the Hybrid CPV
Sarah El Himer,∗ Ali Ahaitouf
Author affiliations
Laboratory of Intelligent Systems, Georesouces and Renewable Energies (SIGER), Faculty of Sciences and Technologies, Sidi Mohammed ben Abdellah University, P.O. Box 2202, Fez, Morocco
* Corresponding author.
sarah.elhimer@usmba.ac.ma (S. El Himer)
alii.ahaiitouf@usmba.ac.ma (A. Ahaitouf)
History: Received 26 August 2020 | Revised 30 October 2020 | Accepted 6 November 2020 | Published online 19 November 2020
Copyright: © 2020 The Author(s). Published by solarlits.com. This is an open access article under the CC BY license (http://creativecommons.org/licenses/by/4.0/).
Citation: Sarah El Himer, Ali Ahaitouf, Improvement of Optical Performances Using the Hybrid CPV, Journal of Daylighting 7 (2020) 238-245. https://dx.doi.org/10.15627/jd.2020.20
Figures and tables
Abstract
Hybrid Concentrated Photovoltaics (HCPVs) are systems in which additional low-cost silicone solar cells are added to take advantage of the power generated by the diffuse radiation lost when using only multi-junction cells that work only with direct radiation. The work has been tested by simulating the performance of a hybrid CPV system composed of a Fresnel lens associated with a pyramid, multi junction cell as well as additional silicon solar cells. This proposal is compared with an ordinary CPV system and a system based on only silicon solar cells. The simulation results show that the CPV makes it possible to have a high optical efficiency of 94% at the pyramid exit for direct radiation, but this high efficiency rapidly decreases to 0% for diffuse radiation. In this case, the silicon solar cell comes into the scene to converts these diffused or non-concentrated rays into electricity, with an optical efficiency of 85%. It was also found that the Hybrid CPV system was able to increase the power by 21% compared to the CPV system.
Keywords
Multi-objective optimization, Radiance, HoneybeePlus, Field Measurements
Nomenclature
| a | Output radius |
| A | Input radius |
| Ain | Entrance aperture area |
| an | Half of the difference between the width of the exit and width of the entrance |
| Aout | Exit or receiver area |
| C | Whole Concentration ratio |
| Cgeo | Geometric concentration ratio |
| CPC | Compound Parabolic Concentrator |
| CCPC | Crossed Compound Parabolic Concentrator |
| D | Fresnel lens diameter |
| DNI | Direct Normal Irradiance |
| f | Focal length of Fresnel lens |
| n | Number of reflections |
| HCPV | Hybrid Concentrated Photovoltaic |
| L | Pyramid length |
| MJ | Multi-junction |
| POE | Primary Optical Element |
| SOE | Secondary Optical Element |
| θi | Entrance angle of the pyramid |
| α | Pyramid angle |
| θ | Opening angle of Fresnel lens |
| ղ | Optical efficiency |
1. Introduction
A CPV system consists of three main elements: a concentration optics that is the core of the CPV system, solar cells and a tracker. Concentration optics can be based on one optical element or two optical elements. Several authors have used a Fresnel lens with different shapes [1-10], others used parabolic mirrors [11] and compound parabolic concentrator [12,13]. Results show that the use of one optical element for CPV systems cannot achieve the overall performances criteria of a CPV system; either the system has a high efficiency while the flux distribution is not homogeneous on the cell, or the opposite. Then the multistage concentrators means concentration systems that use two optical elements, the first stage is named the Primary Optical Element (POE) and the second is the Secondary Optical Element (SOE) can be more efficient. In the literature, we found several systems which are based on the Fresnel lens and the secondaries can be the Crossed Compound Parabolic Concentrator, Pyramid, Hyperbole and Dome, which are studied by Rodríguez et al [14,15], for a targeted concentration ratio of 1000x. Simulation results show that the four concentrators have an optical efficiency greater than 80% and an acceptance angle of ±1°. The best homogeneity of the flux is obtained with the pyramid. Experimental tests validated these results with a fall of the optical efficiency to 73% and the angle of acceptance to ±0.8°. Similar study was performed by El Himer et al. [16] who compared only by simulation and analyzed four CPV systems based on four secondary optical elements (CPC, CCPC, Cone and pyramid) associated with a circular flat Fresnel lens for a concentration ratio of 1000x. They also confirmed that the pyramid as SOE presents the most uniform illumination on the solar cell, the largest acceptance angle (1.4°) and a highest optical efficiency (83%) whatever the used material. Several authors have discussed the performance of parabolic mirrors either as a primary optical element or as a secondary element [17-20]. Results indicate that the use of the parabolic mirror as a primary optical element shows interesting optical performances especially if it is associated with a flat mirror since it presents the best achieved optical efficiency of 85%. The CPV system is more efficient in the case of using two optical elements of concentration since it allows to have an optical efficiency and a high concentration as well as a wide acceptance angle.
Until now, CPV technology uses only direct radiation. Thus, the diffuse radiation is lost. In order to capture diffuse radiation, new designs of CPV modules are being developed.
Photovoltaic architectures with hybrid concentrated photovoltaic (CPV) concerns system which makes it possible to combine CPV modules and low cost solar cells. This combination has the advantage to take benefits from diffused and non-concentrated solar rays.
Figure 1 shows a schematic view of the hybrid CPV architecture. This kind of system used two solar cells, the first and principal cells are kind of a III–V multijunction (MJ), generally three-junctions (3J), solar cell with high efficiencies, and auxiliary low-cost solar cells such as Silicon solar cells. These cells are all together combined into one photovoltaic module with concentrator optics.
Among the authors who are developed this technology, Noboru Yamada and Daiki Hirai [21] have experimentally tested this design and have found in outdoors measurements, under a high DNI (800 W/m2) a power increase of 39% for a module using triple junction solar cells with a bi-facial silicon solar cell. Martínez et al. [22] also tested the outdoor performance of this kind of module and found some preliminary results showing that the concept is capable of converting up to 36.8% of the global solar resource rather than just the direct beam and the hybrid module generates 30% additional power with respect to only the array of concentrator for multi-junctions solar cells alone. In 2010, Benitez et al. [23] proposed a design which involves a primary triple junction solar cell on which the normal direct radiation is concentrated by an optical element and several low cost solar cells surrounding the primary cell, their roles is the reception of the solar radiation from the concentrator missed by the primary cell. Regarding the optical concentrator, they used a Fresnel lens as a typical concentrator. Woo-Lim Jeong et al [24] optimized, analyzed and tested a mirror pyramid as secondary optical element (SOE) associated with a rectangular Fresnel lens for the hybrid CPV modules. They used one triple junction solar cell and 12 polycrystalline silicone solar cells. They reported, as experimental results with their optimized SOE, a maximum output power on the triple-junction cell and polycrystalline silicon cell of 212.8W/m2 and 5.14 W/m2, respectively.
Nguyen Xuan Tien and Seoyong Shin [25] proposed the same technology to improve both the uniformity of irradiation and the efficiency of the system, their system is based on a Fresnel lens as a primary optic associated with a plan - concave lens as a secondary optic to strongly concentrate and homogeneously distribute the flux on a multi-junction solar cell as well as another low cost additional solar cell to collect diffuse solar radiation. The material used to make the Fresnel lens is PMMA and N-BK7 for the plano-convex. The results show that this approach improved both the uniformity of irradiance and increased the optical power ratio by approximately 17.12%. In this paper, we will rely on our previous work [16] in order to choose the pyramid as SOE since it is the most suitable with the Fresnel lens. Because of alignment errors associated with the optical element and cells, the peak optical efficiency for the 3J cell was as low as 94% at normal incidence and dropped to 10% at θ = ~1.8°. For that we suggest to add silicon cells according to the location of the convergent diffuse rays by the Fresnel lens and which do not reach the entrance of the pyramid; the idea is to increase the global efficiency of our system [16].
2. Description of the optical system
In our previous work, we found that the pyramid-based concentrator gives the more uniform irradiance distribution and the high optical efficiency whatever the used material, and the largest tolerance angle.
As primary optical element (POE), we choose the flat circular Fresnel lens which is characterized by its diameter d, its focal length f, its f number, F/# and its θ is the opening angle defined by:
The pyramid (Fig. 2) is a secondary optical element which is inspired from the cone with a rather rectangular shape. It is defined by the output and input radius a, and A, the output and input angle θf and θi, the angle of pyramid α and its length H. The length of the pyramid is dependent on the number of ray reflections, n:
The whole concentration ratio of each CPV system is given:
where Cgeo denotes the geometrical concentration and ղ the optical efficiency. Those parameters are respectively given by:
3. Simulation results
3.1. System based on flat silicon solar cells
In order to judge the performance relevance of our proposal, we compared its obtained power with the one obtained if 16 flat silicon cells are used, all the cells have a dimension of 350×350 mm2, (the same dimension as the Fresnel lens). The irradiance used to measure the optical efficiency is 1000 W/m2. Assuming modest-DNI region. Sunlight rsys were designed with 80% DNI and 20% diffuse light. Figure 3 shows the evolution of the optical efficiency of silicon solar cells. The tilt angle increases η in a slight way as shown in the Fig. 4. This allows us to clearly notice that the tilt angle influences the amount of energy collected by a photovoltaic module. The power obtained for 0° is 212 W/m2.
Although the optical efficiency is high but the efficiency of these silicon solar cells remains a little low (18% outdoor and 33% in the laboratories), this is why we add optical elements to concentrate the solar rays on multi-junction cells in order to increase the power.
3.2. CPV system
The first CPV systems under study is based on a circular flat Fresnel lens with a diameter of 350 mm and a focal length of 265 mm, the Fresnel lens is associated to a refractive pyramid with the following dimensions: the length H = 48 mm, its input aperture of 15.05×15.05 mm2 and the output opening of 10×10 mm2. The geometrical concentration system is generally defined as the ratio of the input aperture (determined by primary lens diameter) and the optics output area (determined by the cell diameter), resulting a geometrical concentration ratio of 1000X.
The material used for manufacturing the Fresnel lens is Polymethyl methacrylate (PMMA, n=1.49) and B270 as material for the refractive pyramid knowing by its high transmission, allows a high impact resistance, provides light diffusion and reduces the hot spots. The simulations are performed by the ray-tracing Trace-Pro software with an incident flux of 1000 W/m2 including wavelength from 0.4 to 1.4µm.
Usually, in addition to direct radiation coming with normal incidence (0°), exists also some diffuse radiations which have a different tilt angles. In this test, we are trying to test our system by including direct radiation and diffuse light. Investigating the incident angle effect on the optical efficiency of this system is an important step in the optical design improvement. Figure 5 illustrates the optical efficiency evolution of this CPV system, defined by the ratio between the flux at the entrance of the Fresnel lens and the exit of the SOE. The optical efficiency at the pyramid exit reached 94% (760 W/m2) at 0°, but this efficiency decreases if the sun's rays arrive with a tilt ±0°. For example, all rays coming with an incident angle of θ = ~1.3°, the optical efficiency dropped to 50%. This is caused by a part of sun rays that don't reach the pyramid and spread away around it from the incident angle of 1.2 °, as shown in Fig. 6. That is also clear in Fig. 7, the flux distributed on the whole pyramid exit at incidence angle of 0°, but for 1.2°, we can see that the flux is distributed over part of pyramid output (from -5 to 1 mm). Concerning the incidence angle of 2°, just some rays with a low intensity reach the pyramid exit. We observe also that under normal light incidence, the flux density is centered around 11×105 W/m2 with some small variations, on the other hand, the rays which come with an angle of incidence greater than 0 °, the intensity decreases and the oscillations are stronger.
Compared the power value of the CPV system with the flat silicon PV for the same size, we find a big difference in power, this is due to the use of multjunction cells more efficient by 45% as efficiency.
Figure 7
Fig. 7. Flux distribution on pyramid exit for different incidence angle of (a) 0°, (b) 1.2°, and (c) 2°.
3.3. Hybrid CPV
To recover the rays that fall out of the pyramid and increase the performance of the CPV system, we add 4 silicon solar cells of (100×100 mm2) in around the exit of the pyramid as shown in Fig. 8. We simulate the system for different incidence angles (from 0 to 20 °) to measure the performances of this hybrid CPV system.
Figure 8
Fig. 8. Model of CPV module and hybrid CPV architecture: (a) schematic view oh hybrid CPV and (b) Simulation of HCPV for an incident angle of 2°.
Figure 9 shows the optical efficiency susceptible to reach the 4 silicon solar cells. We notice that the diffuse light which arrives with inclinations, can reach silicon cells depending on the in cadence angle as follows:
- For -20°≤θ≤-0° the rays reach the cells a and d.
- 0°≤θ≤24° the cells b and c are reached by the rays
- θ=0° all rays are collected at the pyramid output
- -2°≤θ<0 part of light reaches the pyramid exit and the other part falls on cells a and d
- 0<θ≤2 part of light reaches the pyramid exit and the other part falls on cells b and c
Note that the optical efficiency is higher when the rays are perpendicular to the Fresnel lens surface (94%), but the optical efficiency in the case of diffuse radiation reaching the silicon cells reaches 75% and it remains stable until 20°, then it begins to decrease. This implies that the optical efficiency of the mini-module is improved compared to the results of previous section (CPV system). For the proposed system the power achieved is 947 W/m2. We can say that the performance of this system is improved by 20% for 0°.
Figure 10
Fig. 10. Flux distribution on Si solar cells at incident angle of (a) -2°, (b) 2°, (c) -10°, (d) 10°, (e) -20°, and (f) 20°.
Figure 10 shows the flux distribution on the silicon cells. We notice that the flux is concentrated around the pyramid exit for -2°≤θ≤ 2° and by increasing the incidence angle, the flux drifts away towards the Si cells, and it is normal to have this distribution because the rays which do not reach the pyramid they arrive with angles more than 2 ° fall on one of the four Silicon solar cells. Although the parts of the placed silicon solar cells that are next to the SOE were affected by the shadow of the SOE, but they still collected the highest intensity (95000 W/m2). In addition, the parts placed away from the CPV also showed radiation of at least by absorbing diffuse light.
3.4. Hybrid CPV surrounded by mirrors
In this part, we propose to add four mirrors, between the Fresnel lens and Si solar cells as shown in Fig. 11, to increase both the power of the hybrid system and its angular tolerance. This is a limit case, useful for large incidence angle, where for instance the tracker stoops his solar following. Figure 12 illustrates the optical efficiency reaching the four Silicon cells, we notice that:
- For θ=0°, the rays are collected by the pyramid, that’s why the optical efficiency at pyramid exit reach 94%.
- For -2°≤θ<0 part of light is caught by the pyramid and the other part falls on cells a and d, we can observe that the optical efficiency on pyramid exit decreases from 94 to 0%, by against, it increases from 0 to 85% on cells a and d and symmetrical situation is produced for negative corresponding angle with silicon cell c and d.
- -60°≤θ≤-0° In this case, all the rays fall on cells a and d with an optical efficiency of 85%, and symmetrical situation occurs for cells c and d for positive similar angles.
Calculating the power achieved by this system is 972.5 W/m2, and then we have an increase of 21.86% compared to the system without mirror.
Figure 13 shows the simulation results for the four silicon solar cells; we observe that by adding the mirrors, the flux is distributed in a larger surface compared to the Fig. 9, but they are distributed on the same behavior, the parts of the placed silicon solar cells that are next to the SOE were affected by the shadow of the SOE, but they still collected the highest intensity (1×106 W/m2), and the other side experienced an increase in intensity from 5×105 W/m2 (Fig. 10) to 15×105 W/m2. Concerning the irradiance, the results are sketched in Table 1. As we see, the silicon cells Si, a and Si, d, have high irradiance for an angle of incidence -2°≤θ, and silicon cells Si, b and Si, c, have high irradiance for an angle of incidence θ≥2.
Figure 13
Fig. 13. Flux distribution on Si solar cells at incident angle of (a) -20°, (b) 20°, (c) -45°, (d) 45°, (e) -60°, and (f) 60°.
3.5. Discussion
Table 2 presents a comparison of the optical performances of our system compared to results obtained by Yamada et al [1] and Jeong et al [4] systems. We can see that our system has a high optical efficiency and power compared to other studies at pyramid exit and the silicon cell.
4. Conclusion
In this paper, we have presented performances and investigations of a hybrid CPV based on Fresnel lens and a pyramid as secondary optical elements. We demonstrated by simulation results that by hybridization of CPV, increases the optical efficiency especially when the rays are perpendicular to the Fresnel lens surface (94%), but the optical efficiency in the case of diffuse radiation reaching the silicon cells reaches 75% and it remains stable until 20°, then it begins to decrease. For the proposed system the power achieved is improved by 20%. And by adding mirror, this power is increased by 21.86%.
Contributions
S. El Himer: conceptualization, methodology, and writing original draft. A. Ahaitouf: supervision, writing-review, and editing.
Declaration of competing interest
The authors report no conflicts of interest.
References
- S. El Himer, A. Ahaitouf, sara El-yahyaoui, abdellah Mechaqrane, Performance analysis of non-imaging Fresnel lens as a primary stage for CPV units, IOP Conference Series: Earth and Environmental Science (2018) 012029. https://doi.org/10.1088/1755-1315/161/1/012029
- R. Leutz, A.Suzuki A. Akisawa, T. Kashiwagi, Design of a nonimaging Fresnel lens for solar concentrators, Solar energy 65 (1999) 379–387. https://doi.org/10.1016/b978-008043895-5/50228-9
- A. Akisawa, M. Hiramatsu, K. Ozaki, Design of dome-shaped non-imaging Fresnel lenses 3 taking chromatic aberration into account, Solar Energy 86 (2012) 877–885. https://doi.org/10.1016/j.solener.2011.12.017
- T. T. Pham, Ngoc Hai Vu, and S. Shin, Design of curved fresnel lens with high performance creating competitive price concentrator photovoltaic, Energy Procedia 144 (2018) 16–32. https://doi.org/10.1016/j.egypro.2018.06.004
- F. Languy, C. Lenaerts, J. Loicq, T. Thibert, S. Habraken, Performance of solar concentrator made of an achromatic Fresnel doublet measured with a continuous solar simulator and comparison with a singlet, Solar Energy Materials and Solar Cells (2013) 70–76. https://doi.org/10.1016/j.solmat.2012.10.008
- G. Vallerotto, M Victoria, S Askins, I Antón, and G Sala, Experimental characterization of achromatic doublet on glass (ADG) Fresnel lenses, AIP Conference Proceedings 1881 (2017) 030010. https://doi.org/10.1063/1.5001421
- Z. Zhuang, F.eihong Yu, Optimization design of hybrid Fresnel-based concentrator for generating uniformity irradiance with the broad solar spectrum, Optics & Laser Technologys 60 (2014) 27. https://doi.org/10.1016/j.optlastec.2013.12.021
- G. Wang, Z. Chen, P. Hu, X. F. Cheng, Design and optical analysis of the band-focus Fresnel lens solar concentrator, Applied Thermal Engineering 102 (2016) 695–700. https://doi.org/10.1016/j.applthermaleng.2016.04.030
- K. Ryu, J.G. Rhee, K.M. Parkc, J. Kim. Concept and design of modular Fresnel lenses for concentration solar PV system, Solar energy 80 (2006) 1580–1587. https://doi.org/10.1016/j.solener.2005.12.006
- T. T. Pham, N. H. Vu and S. Shin, Novel Design of Primary Optical Elements Based on a Linear Fresnel Lens for Concentrator Photovoltaic Technology, Energies 12 (2019) 1209. https://doi.org/10.3390/en12071209
- K.K. Chong, F.L. Siaw, C. W. Wong, G.S.Wong, Design and construction of non-imaging planar concentrator for7 concentrator photovoltaic system, Renewable Energy 34 (2009) 1364-1370. https://doi.org/10.1016/j.renene.2008.09.001
- M. Tian, Y. h. Su, H. feiZheng, G. Pei, G. Li, S. Riffat, A review on the recent research progress in the compound parabolic concentrator (CPC) for solar energy applications, Renewable and Sustainable Energy Reviews 82 (2018) 1272-1296. https://doi.org/10.1016/j.rser.2017.09.050
- Y. Yu, N. Liu, G. Li, R. Tang, Performance comparison of CPCs with and without exit angle restriction for concentrating radiation on solar cells, angle restriction for concentrating radiation on solar cells, Applied energy 155 (2015) 284-293. https://doi.org/10.1016/j.apenergy.2015.06.012
- J. P. F.Rodríguez, H. Baig, E. F.Fernández, F. Almonacid, T. Mallick, P.P. Higueras, Optical modeling of four Fresnel-based high-CPV units, Solar Energy 155 (2017) 805-815. https://doi.org/10.1016/j.solener.2017.07.027
- J. P.F.Rodríguez, E. F.Fernández, H. Baig, F. Almonacid, T. Mallick, P.P.Higueras, Development, indoor characterisation and comparison to optical modelling of four Fresnel-based high-CPV units equipped with refractive secondary optics. Solar Energy Materials and Solar Cells 186 (2018) 273-283. https://doi.org/10.1016/j.solmat.2018.06.050
- S. El Himer, A. Ahaitouf, S. El-yahyaoui, A. Mechaqrane, Parametric optimization and performances analysis of four secondary optical elements for concentrator photovoltaic systems, International Journal of Renewable Energy Research-IJRER 8 (2018) 4. https://doi.org/10.1063/1.5053502
- S. Lokeswaran , T. K. Mallick , K.S. Reddy, Design and analysis of dense array CPV receiver for square parabolic dish system with CPC array as secondary concentrator, Solar Energy 199 (2020) 782-795. https://doi.org/10.1016/j.solener.2020.02.075
- F. Trespidi and G. Timò, Optical Design of an Off-axis Mirror Based Solar Concentrator, in: AIP Conference Proceedings 1881 (2017) 030008. https://doi.org/10.1063/1.5001419
- F. Trespidi, E. Malvisi, and R. Parmesani, Shape characterization of the primary mirror of a mirror based solar concentrator, in: AIP Conference Proceedings 1881 (2017) 030009. https://doi.org/10.1063/1.5001420
- J. P. F.Rodríguez, E. F. Fernández, Á. F.Solas, F. Almonacid, D. L. Talavera, P. P.Higueras, Optimization of an ultra-high CPV Cassegrain-Koehler unit with 2000_ concentration ratio, in: AIP Conference Proceedings 2149 (2019) 070004. https://doi.org/10.1016/j.enbuild.2017.01.048
- N.A.Yamada, Maximization of conversion efficiency based on global normal irradiance using hybrid concentrator photovoltaic architecture, Progress in Photovoltaics: Research and Applications 24 (2016) 846-854. https://doi.org/10.1002/pip.2765
- J. F. Martinez, M. S. 4-terminal CPV module capable of converting global normal irradiance into electricity, in: AIP Conference Proceedings (2018) 090005. https://doi.org/10.1063/1.5053543
- P. A. Benitez, Photovoltaic concentrator with auxiliary cells collecting diffuse radiation, Google Patents, 2010.
- W.L Jeong, Optimization of the Secondary Optical Element of a Hybrid Concentrator Photovoltaic Module Considering the Effective Absorption Wavelength Range, Applied Sciences 10 (2020) 2051. https://doi.org/10.3390/app10062051
- Nguyen Xuan Tien and Seoyong Shin, A Novel Concentrator Photovoltaic (CPV) System with the Improvement of Irradiance Uniformity and the Capturing of Diffuse Solar Radiation, Appl. Sci. 6 (2016) 251. https://doi.org/10.3390/app6090251
Copyright © 2020 The Author(s). Published by solarlits.com.
 HOME
HOME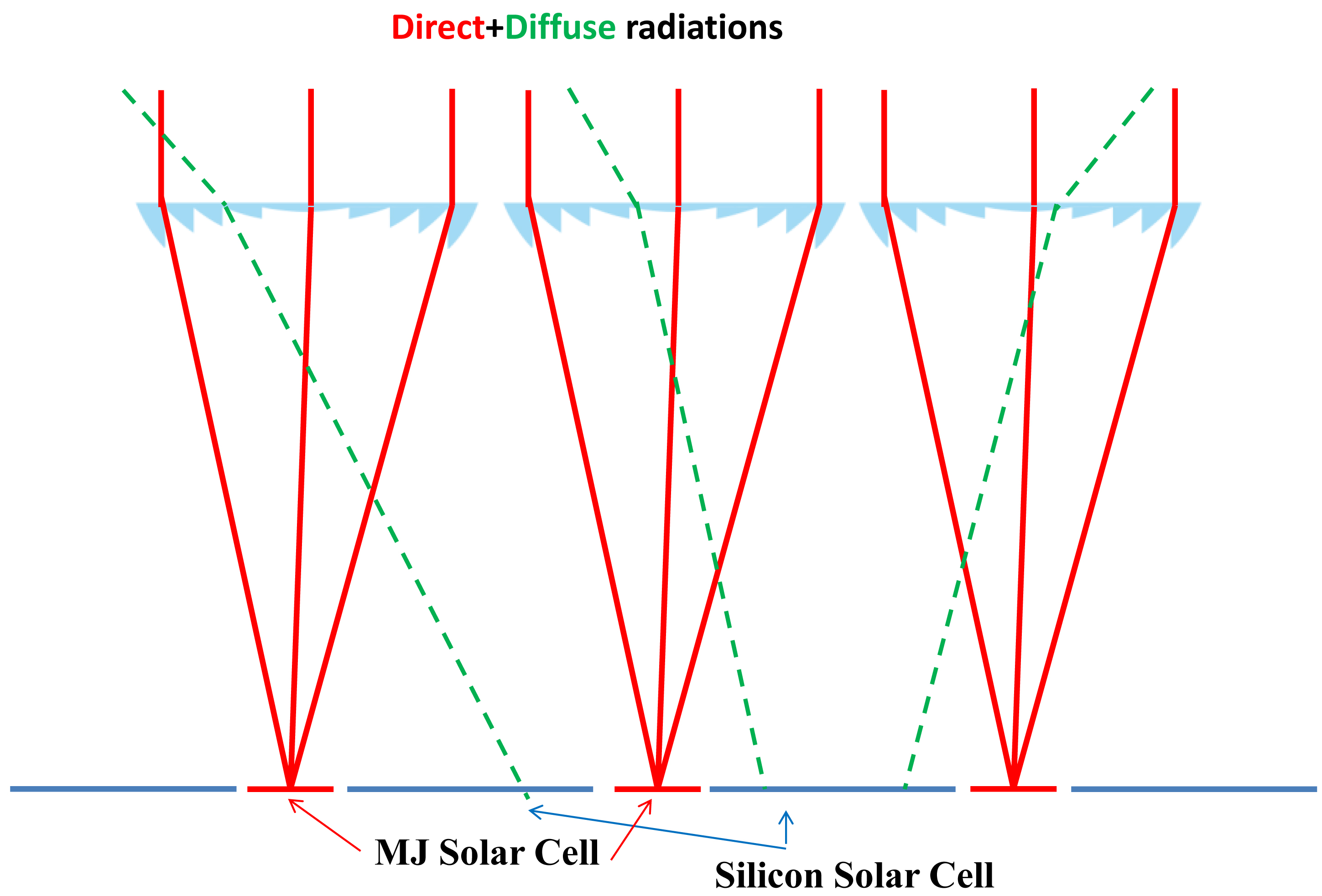 Figure 1
Figure 1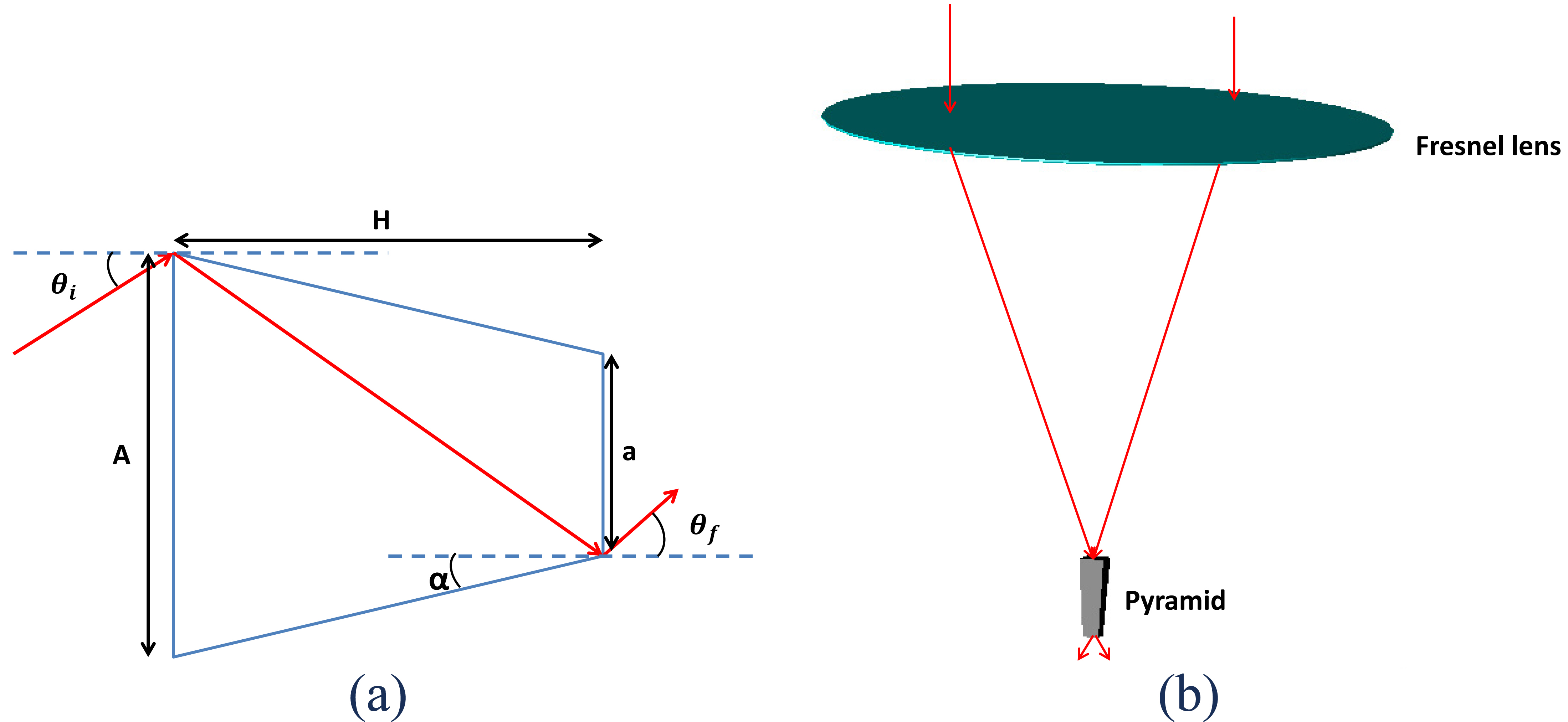 Figure 2
Figure 2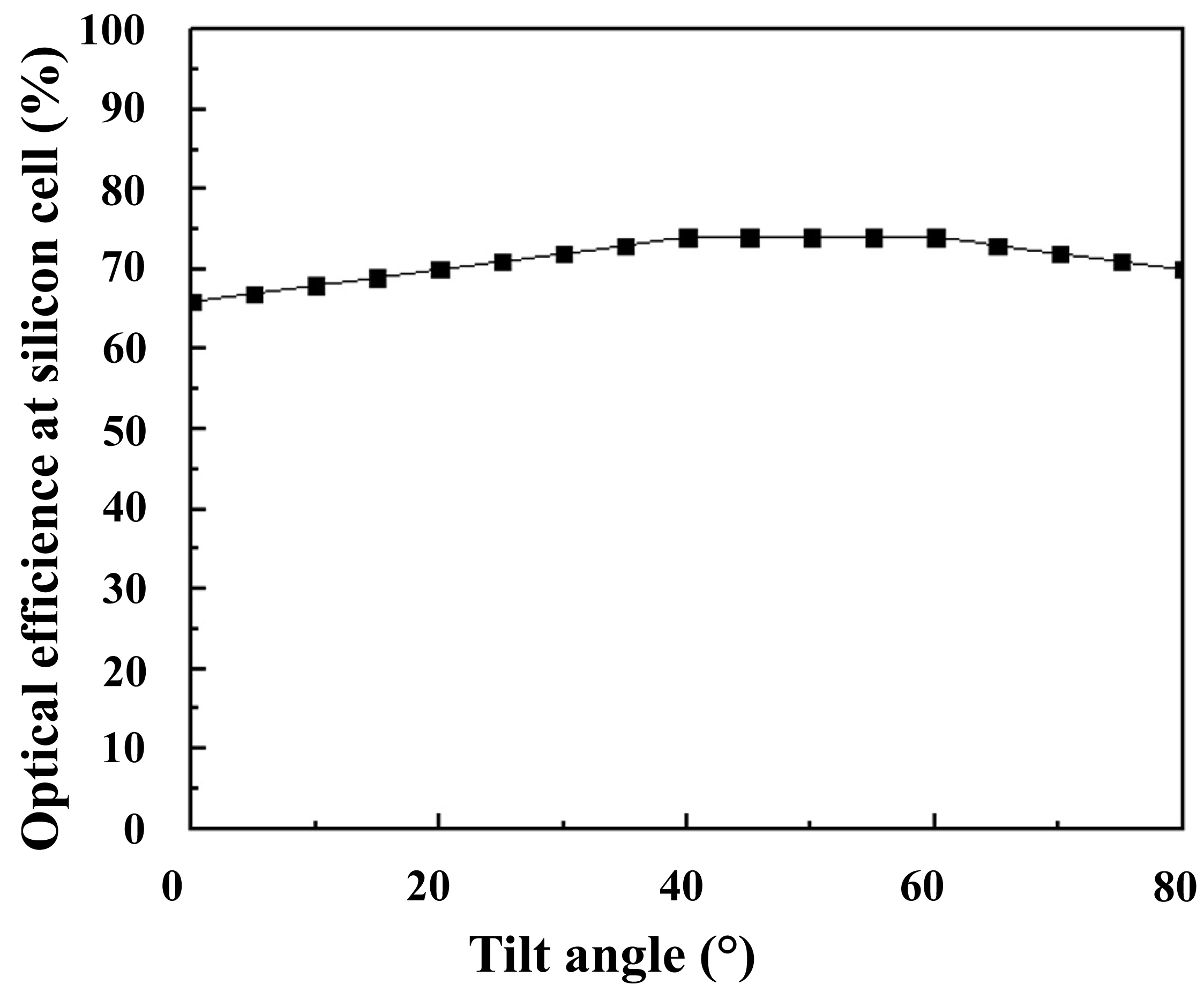 Figure 3
Figure 3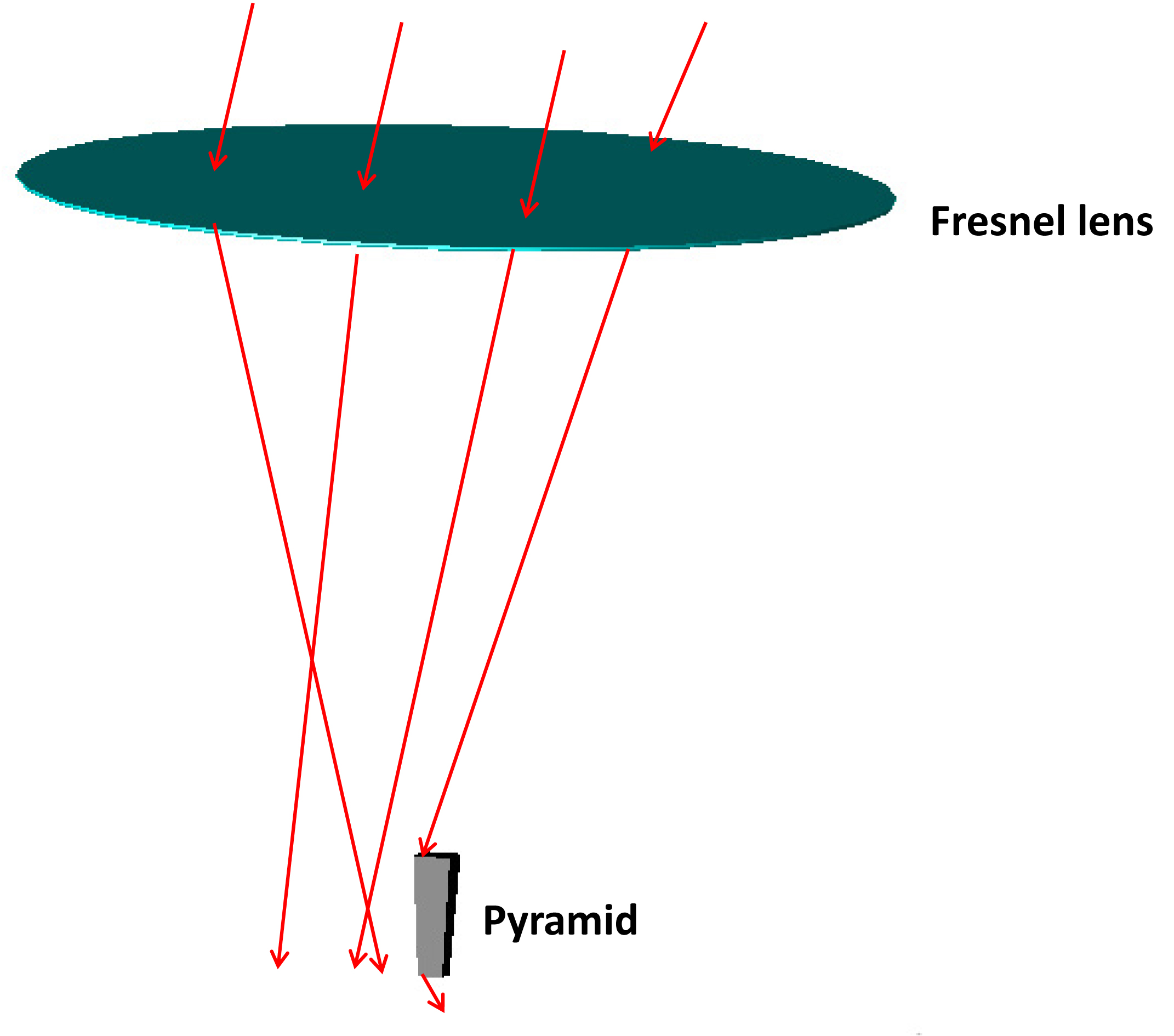 Figure 4
Figure 4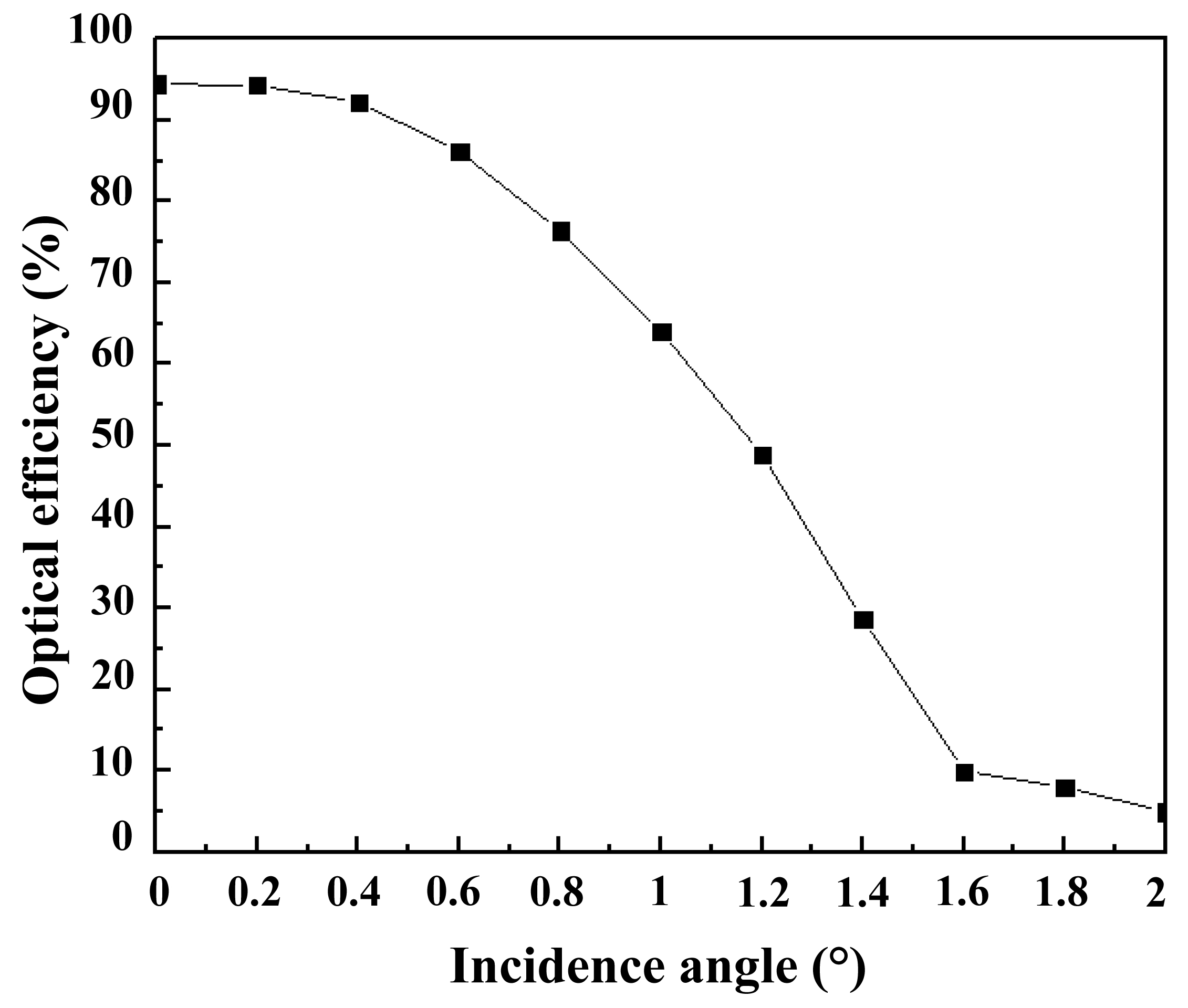 Figure 5
Figure 5 Figure 6
Figure 6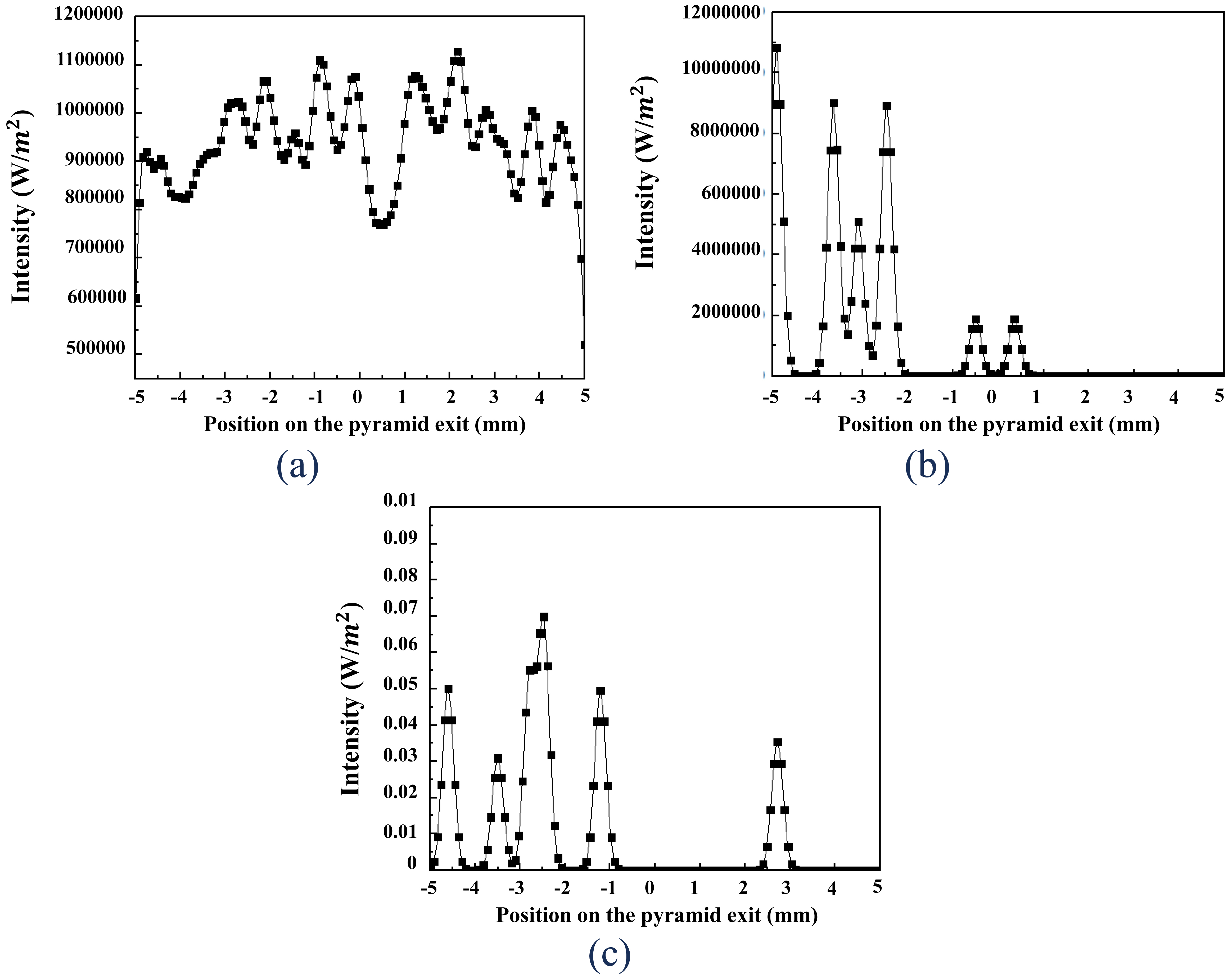 Figure 7
Figure 7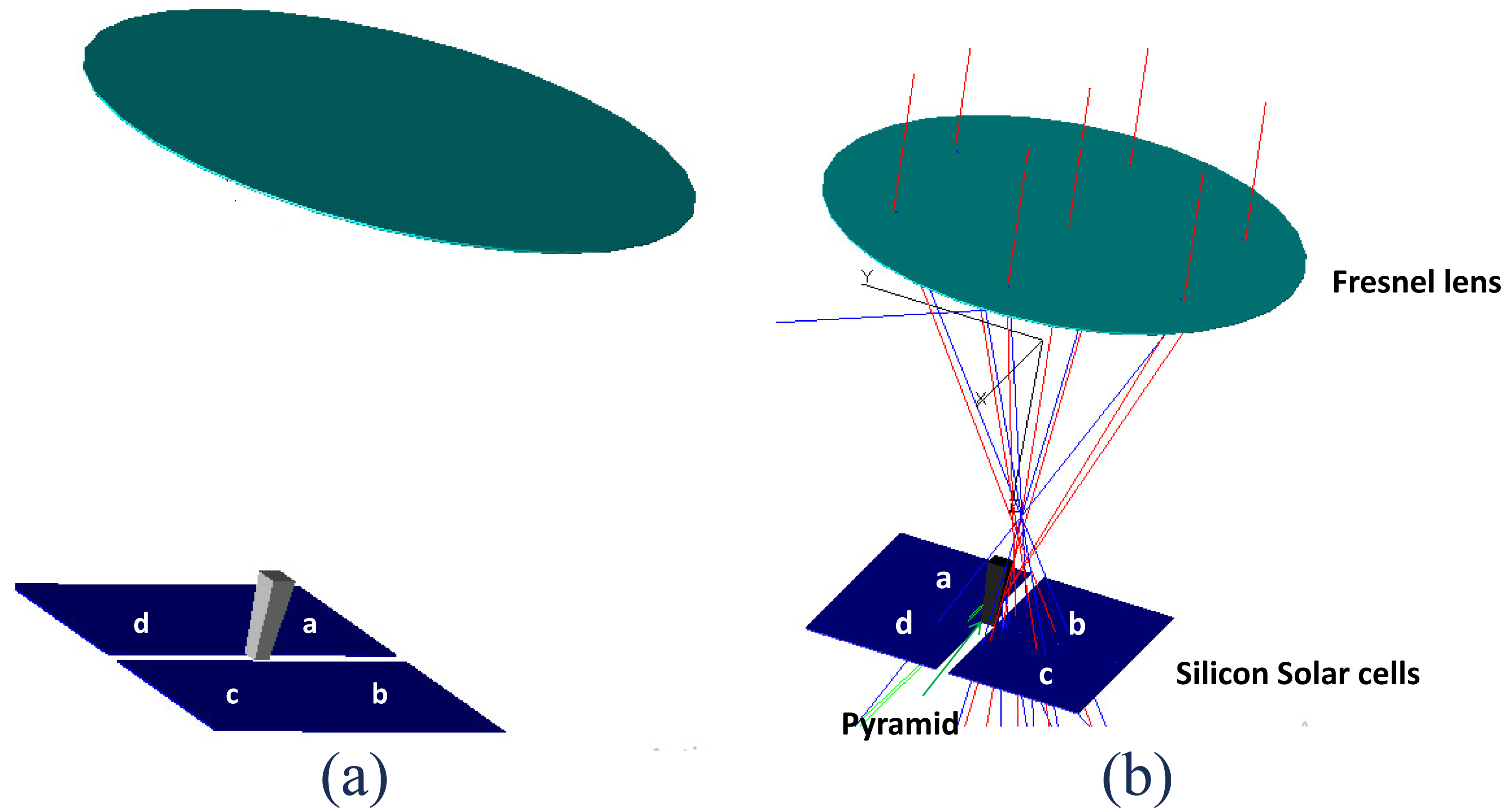 Figure 8
Figure 8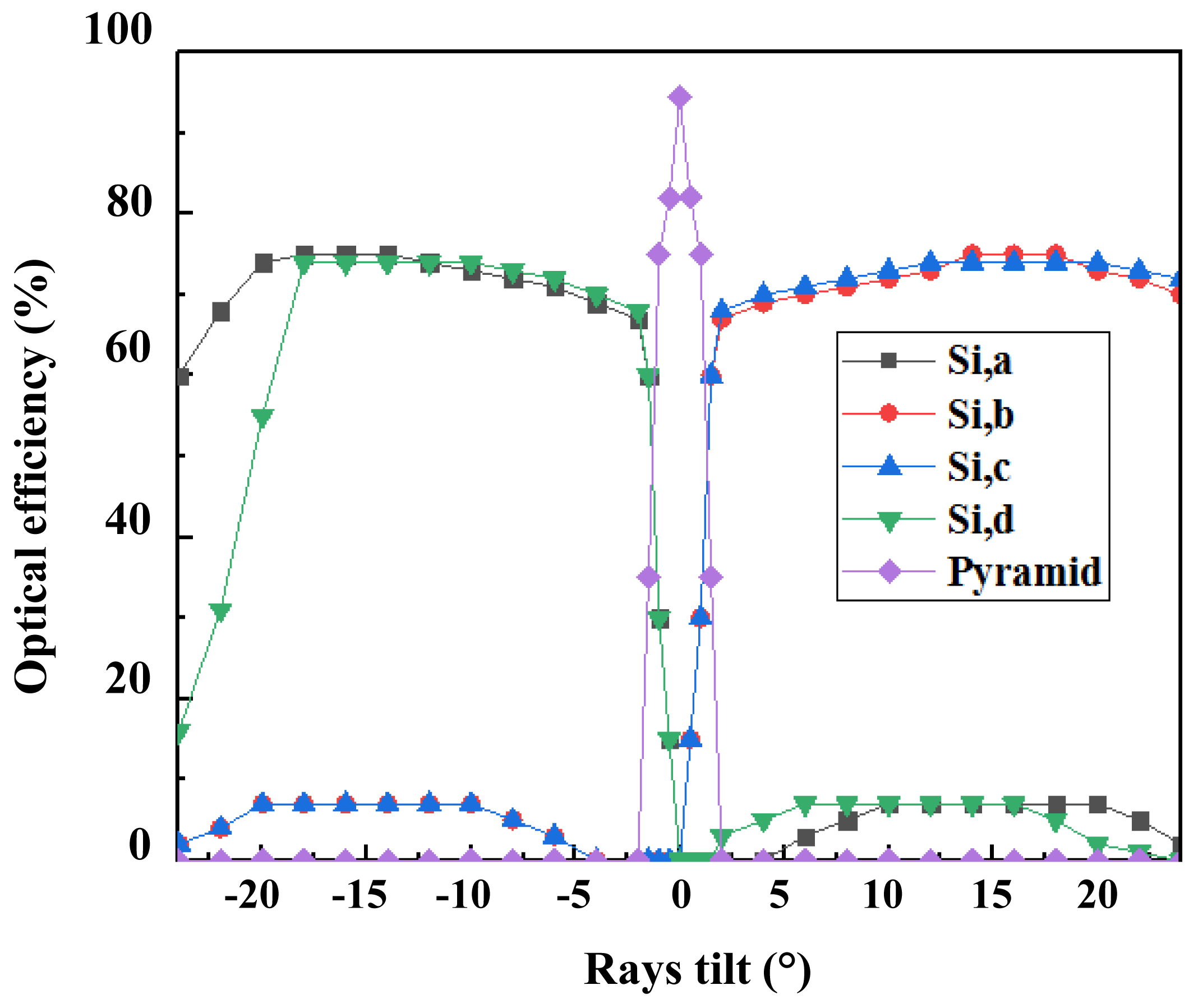 Figure 9
Figure 9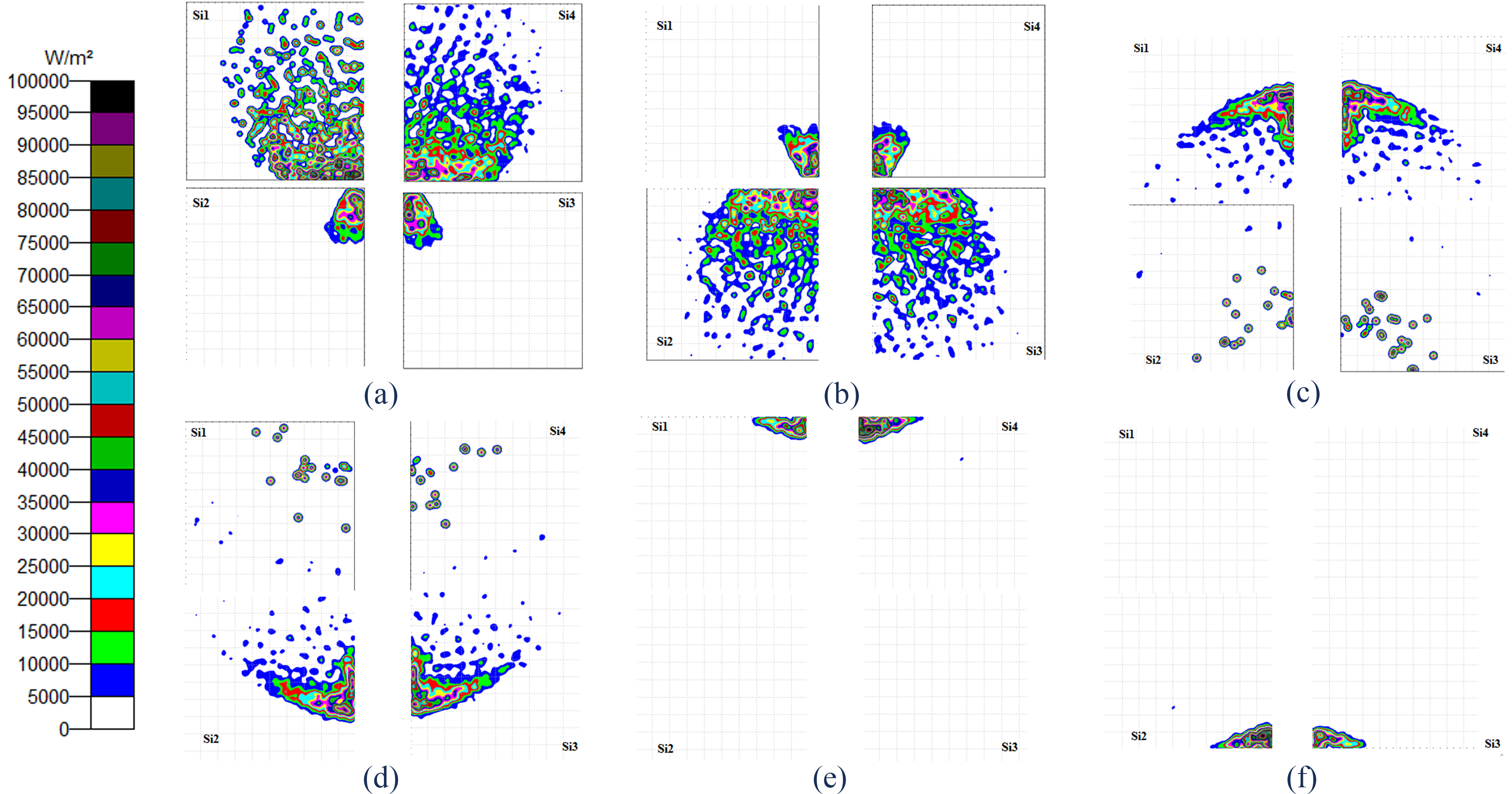 Figure 10
Figure 10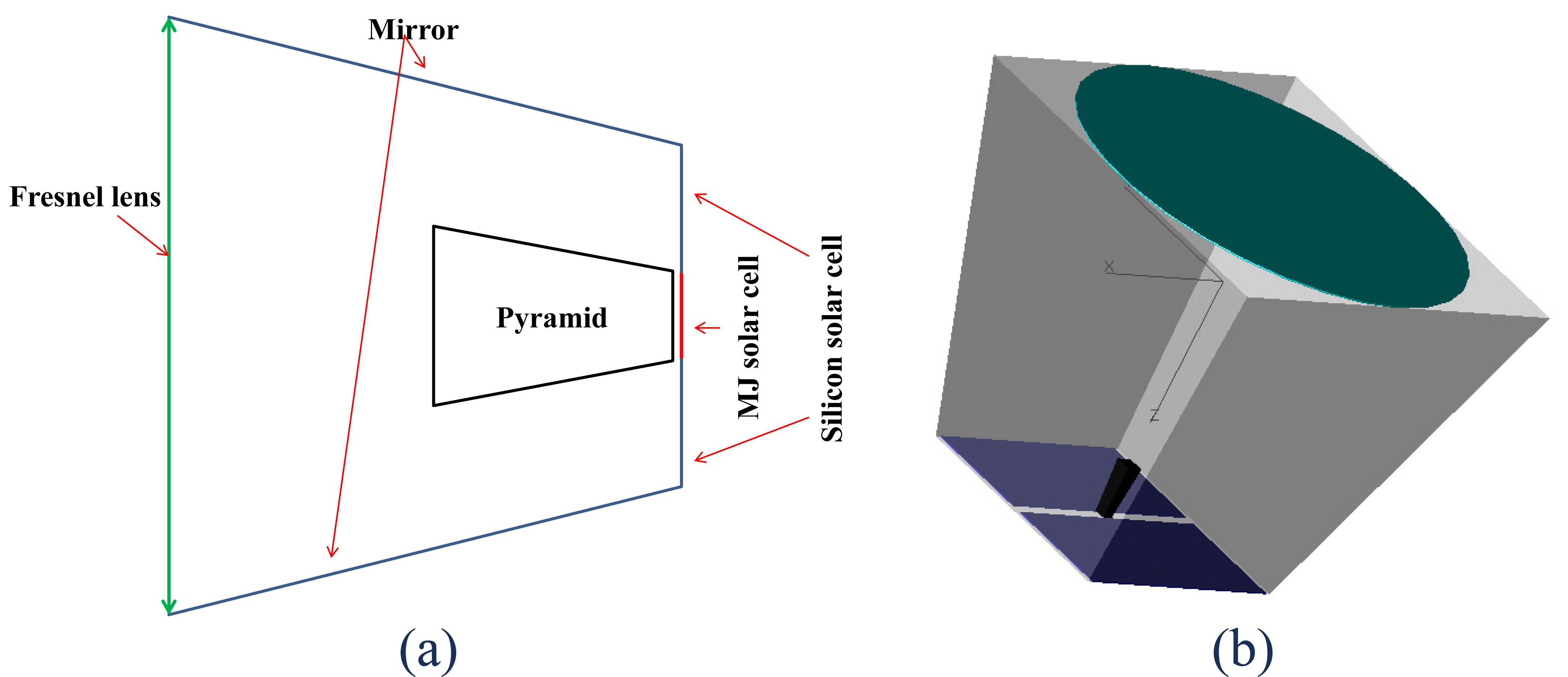 Figure 11
Figure 11 Table 1
Table 1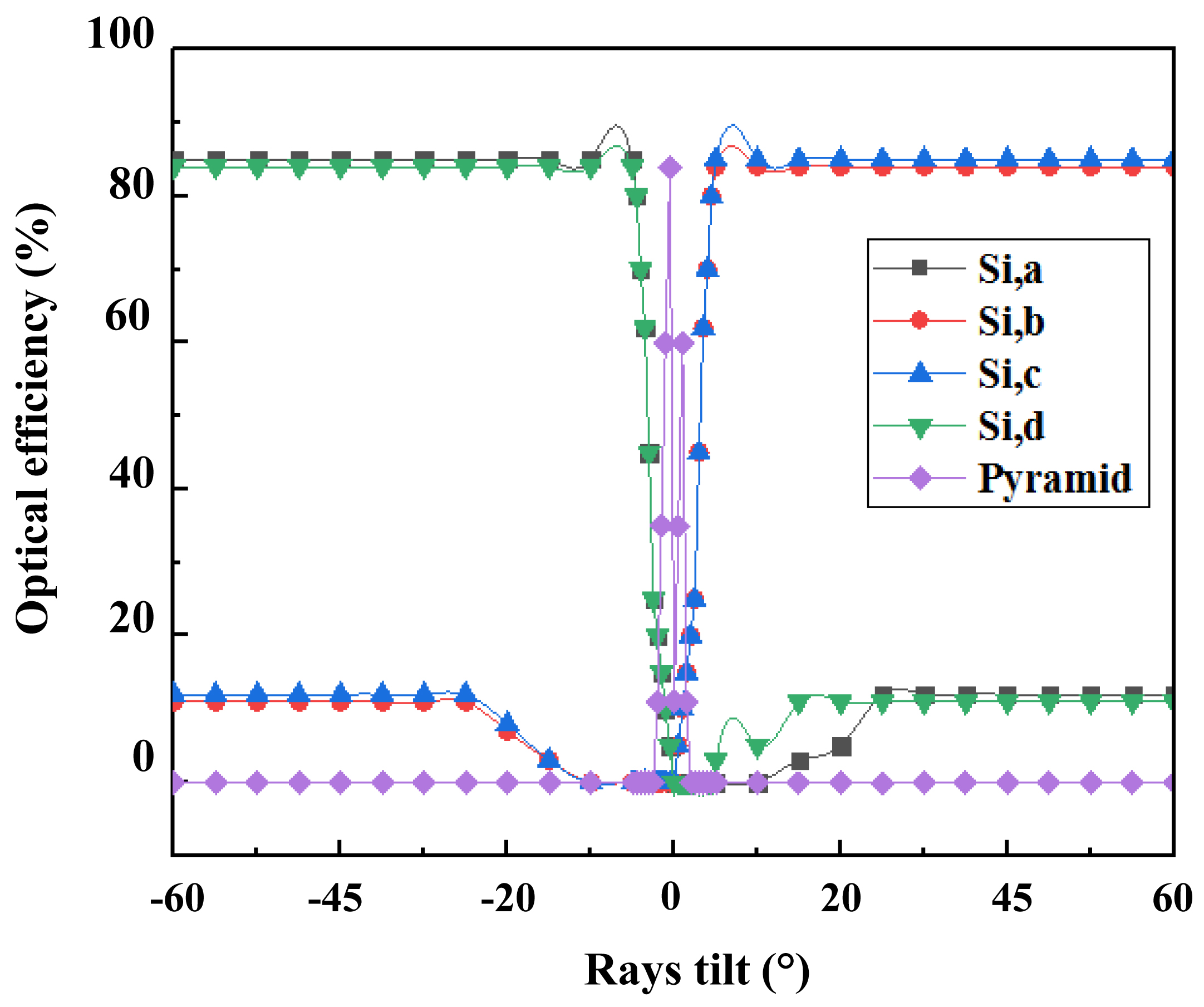 Figure 12
Figure 12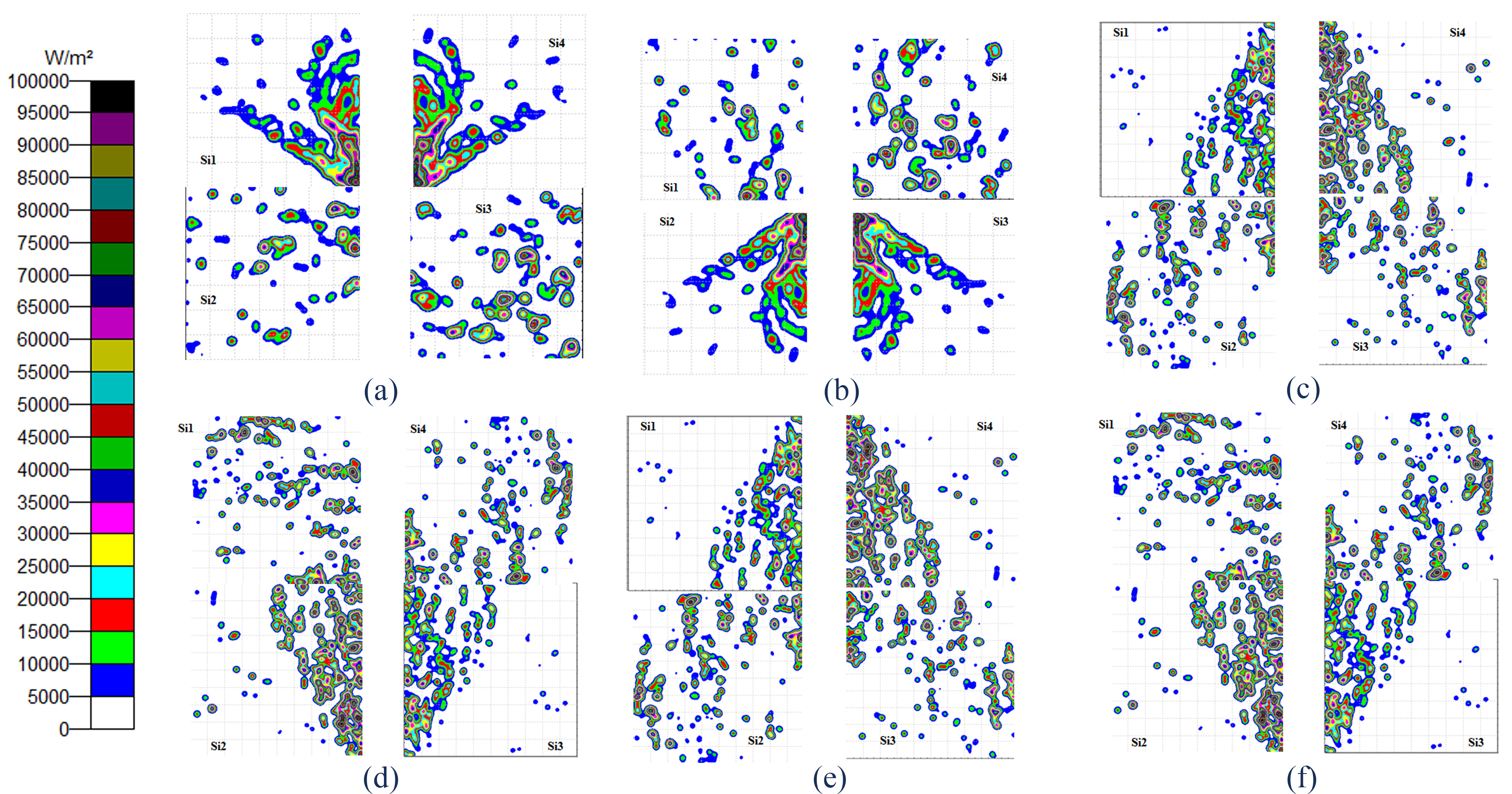 Figure 13
Figure 13 Table 2
Table 2