Volume 8 Issue 1 pp. 100-109 • doi: 10.15627/jd.2021.7
Optical Analysis of a New Solar Distiller with Cylindrical Surface Concentrator and Vertical Gap Evaporator
Jinglian Zhao,a Hongfei Zheng,a Shen Liang,a Fangzhou Liu,a Ge Wang*,a,b
Author affiliations
a School of Mechanical Engineering, Beijing Institute of Technology, Beijing, 100081, China
b School of Physics and Electronics, Nanning Normal University, Nanning, 530001, China
*Corresponding author.
328502439@qq.com (J. Zhao)
hongfeizh@bit.edu.cn (H. Zheng)
liangshen09@163.com (S. Liang)
Liufangzhou1996@126.com (F. Liu)
11720194@qq.com (G. Wang)
History: Received 21 October 2020 | Revised 10 January 2021 | Accepted 22 January 2021 | Published online 24 February 2021
Copyright: © 2021 The Author(s). Published by solarlits.com. This is an open access article under the CC BY license (http://creativecommons.org/licenses/by/4.0/).
Citation: Jinglian Zhao, Hongfei Zheng, Shen Liang, Fangzhou Liu, Ge Wang, Optical Analysis of a New Solar Distiller with Cylindrical Surface Concentrator and Vertical Gap Evaporator, Journal of Daylighting 8 (2021) 100-109. https://dx.doi.org/10.15627/jd.2021.7
Figures and tables
Abstract
In this paper, a new solar distiller floating on ocean with cylindrical surface concentrator and vertical gap evaporator is proposed for solving the problem of freshwater shortage in islands. When the distiller is floating on ocean, the vertical gap will fill with seawater automatically due to the siphon effect of hydrophilic material. Then the seawater is heated to generate vapor when the incidence sunlight is concentrated to the gap by the cylindrical concentrator. Finally, the vapor reaches the arched transparent glass at the top of the device and condenses to produce fresh water. Optical simulation for the solar distiller is carried out to find the optimal radius of the cylindrical concentrator and the height of the vertical gap. The results indicate that when the radius and height is 6 cm and 5 cm respectively, 80% of the sunlight number within the incidence angle of 45° can be captured by the seawater in the vertical gap. The annual optical performance of the distiller is analyzed for the region within 17° north latitude. As the result, the device placed in east-west direction possesses superior performance. There are more than 10 working hours and 5 working hours in which the reception rate is more than 80% in summer solstice and winter solstice respectively. In autumnal equinox, there are more than 11 working hours with the reception rate exceeding 90%. Energy balance analysis for the whole system is carried out and the stable evaporation rate per unit solar collector area increases gently from 0.12 g/ (m2‧s) to 0.65 g/(m2‧s) when the solar irradiance increases from 500 W/m2 to 1000 W/m2.
Keywords
Solar distillation, Cylindrical surface concentrating, Vertical gap evaporation, Floating type
Nomenclature
| r | Radius (mm) |
| θ | Light incidence angle (o) |
| h | Height of the gap (mm) |
| α | Altitude angle (o) |
| β | Opening angle (o) |
| ηr | Reception rate |
| Q | Energy density (W/m2) |
| γ | Solar azimuth angle (o) |
| h1 | Coefficient of convective heat transfer between the ambient and top arched transparent glass (W/m2‧K) |
| h2 | Coefficient of convective heat transfer between air in the condensation cavity and top transparent glass (W/m2‧K) |
| h3 | Coefficient of convective heat transfer between air in the condensation cavity and surface of condensation cavity (W/m2‧K) |
| h4 | Coefficient of convective heat transfer between the condensation cavity and evaporation surface (W/m2‧K) |
| h5 | Coefficient of the convective heat transfer between air in the concentration cavity and vertical gap (W/m2‧K) |
| hfg | Latent heat of water (W/m2‧K) |
| P2 | Water vapour saturated pressure at T2 (Pa) |
| P5 | Water vapour saturated pressure at T5 (Pa) |
| Ɛ1 | Emissivity of top transparent glass |
| Ɛ2 | Emissivity of evaporation surface |
| F31 | View factor between top transparent glass and evaporation surface |
| Id | Solar irradiances (W/m2) |
| τ1 | The transmittance of the top transparent glass |
| τ2 | The transmittance of the concentration cavity |
| ρ | The reflectivity of the reflective surface |
| Me | Evaporation rate per unit aperture solar collector area (g/m2‧s) |
| T1 | The ambient temperature (K) |
| T2 | Evaporation surface temperature (K) |
| T3 | The average temperature of concentration cavity (K) |
| T4 | The average temperature of the condensation cavity (K) |
| T5 | The average temperature of the top arched transparent glass (K) |
| A1 | Area of top arched transparent glass (m2) |
| A2 | Area of the contact surface between the concentration cavity and condensation cavity (m2) |
| A3 | Area of evaporation surface (m2) |
| A4 | Area of the contact surface between the concentration cavity and vertical gap (m2) |
| Qsi,1 | Total energy entering the system (W) |
| Qsi,2 | Solar energy flux absorbed by the concentration cavity (W) |
| Qsi,3 | Solar energy flux absorbed by the vertical gap (W) |
| Qsi,4 | Solar energy flux absorbed by the surface of condensation cavity (W) |
| Qcv,2,4 | Convective heat flux of air in the condensation cavity and evaporation surface (W) |
| Qcv,3,4 | Convective heat flux of the air in the condensation cavity and surface of concentration cavity (W) |
| Qcv,4,5 | Convective heat flux of the air in the condensation cavity and surface of condensation cavity (W) |
| Qcd,2,3 | Conduction heat transfer from vertical gap to concentration cavity (W) |
| Qcv,2,3 | Convective heat flux of air in the concentration cavity and vertical gap (W) |
| Qcv,5,1 | Convective heat flux of the external environment and surface of condensation cavity (W) |
| Qr,5,2 | The radiation heat transfer of the surface of condensation cavity and evaporation surface (W) |
| Qcds | Heat produced by evaporation of seawater (W) |
1. Introduction
The shortage of freshwater has always been a big dilemma for the economic and social development of some regions, especially in islands and some coastal areas. Facing the above challenge, it is of great significance to utilize rich seawater and solar radiation resources in these regions to produce freshwater. Distillation is one of the simplest forms of solar desalination.
Different scholars have adopted different distillers to improve freshwater production. Thermal and optical analysis indicates that optimizing the parameters of the concentrator such as the shape and size can enormously improve the light reception rate [1]. Goswami et al. [2] used a triangular concentrator to collect the solar radiation on the two sides of the absorber so as to obtain the high evaporation temperature. Jebasingh et al. [3] gave an assessment for the potential possibility of applying parabolic concentrator in seawater desalination. It is indicated that the performance of the distiller with parabolic concentrator will be improved due to the elevation of evaporation temperature. Chaouchi et al. [4] combined a parabolic dish concentrator with a solar still and built a small solar desalination unit. The operating temperature of this unit is improved significantly, and its theoretical efficiency and experimental efficiency reached 68% and 42% respectively. Furthermore, with a much larger reception angle range, compound parabolic concentrator (CPC) and cylindrical concentrator (CC) have been adopted in various stills [5,6]. For example, Yadav et al. [7] combined a compound parabolic concentrator with a solar still, thereby increasing the thermal efficiency of the system to 43.2%.
In order to further assess the optical characteristics of the solar concentrators in complex structures, the computer-aided optical simulation method has been extensively used to calculate the primary parameters [8]. A concentrator with a different deformation ratio was proposed by Liang et al. [9]. And the key parameters of the concentrator including concentrator ratio, light reception rate and maximum energy density were calculated with respect to deformation rate. Similarly, Liu et al. [10] optimized the structure of a multi-surface solar concentrator by raising the height of the involute through the optical simulation. Eventually, the average light reception rate of 0.868 can be achieved.
The development of stills and concentrators in large scale and complex structure indeed help to improve the efficiency of the system. But those distillers will take up too much land area, causing an extra cost. In order to reduce the land occupation and simplify the pipeline system, some scholars propose various floating solar distillation units and apply it to marine agriculture. Wang et al. [11] proposed the concept of floating solar desalination membrane, designed and optimized the concentrating system by optical simulation. As a result, a more reasonable structure of the concentrating system, including concentrator size and concentration ratio, is obtained and applied to seawater desalination. For lessening the device size and shortening mass transfer distance, Shafieian et al. [12] used the heat pipe instead of seawater tank as an evaporation and condensation vessel. It is found that reasonable matching of concentrator and heat pipe can improve the efficiency of seawater desalination. Thus, to say, a combination of solar energy concentrating technology with seawater distillation technology, several special solar desalination devices can be designed. So far, the existing systems are still energy consuming, occupation uncontrollable and not constructive to the promotion to the remote area.
To make the distiller system more compact, the vertical interface finite space can further simplify the process of seawater collection, evaporation and condensation [13]. Generally, capillary or hydrophilic material can be filled into the interface finite space to draw the transportation and accumulation of seawater. When a conventional seawater tank is occupied, the seawater is driven by the capillary force at the evaporation surface rather than the pumping power [14,15]. Furthermore, trapped in the micro-pores narrow channel with lower thermal conduction and convection effect, the seawater is favorable for effective steam generation and desalination by localized heating. Particularly, modified by functional materials on the interface, the evaporation performance can be significantly enhanced [16]. For example, a low-grade heat-driven desalination system is proposed. The system combines with an open-loop heat pipe and capillary effect without any additional mechanical energy input, achieving the thermal conversion efficiency of 65.2% at a heat source temperature of 34 oC and 90.7% at 60 oC [17]. Moreover, solar-driven interfacial evaporation has attracted more attention. And solar absorbers, evaporation structures, thermal insulators and thermal concentrators are considered as the parameters for optimization [18]. However, most of the existing researches are focused on the capillary. But the researchers put less emphasis on a two-dimensional vertical gap used in many practical situations [19,20]. The two-dimensional structure leads to a reduction of solar radiation absorption, thereby the reduction of the reception rate and freshwater productivity. Both the style of concentrator and structure of vertical gap have an interacted influence on the efficiency of the unit, but the potential effect and underway optimization are less reported. Furthermore, to make the desirable distiller applicable for practical purposes, the energy density and reception ratio of the concentrator and water productivity during the whole year need further assessment [21].
Therefore, a new solar distiller floating on the ocean with cylindrical surface concentrator and vertical gap evaporator is proposed, which does not occupy the valuable land area and provides fresh water for coastal residents. The device uses a cylindrical concentrator to concentrate light into the vertical gap to heat the seawater directly, which can significantly improve the evaporation efficiency of seawater and effectively reduce the heat loss in transportation. With an integrated design, the device behaves simple and compact in structure, which becomes convenient to assemble or build and beneficial for heat preservation. Aiming at this device, the optical simulation and optimal design of the concentrating system are carried out under different structures of concentrator and heights of the gap. The annual concentrating performance and stable evaporation rate per unit aperture solar collector area within the region of 17° north latitude is analyzed which provides the theoretical basis for this kind of floating solar seawater desalination.
2. Working principle
The structure of the solar distiller with cylindrical surface concentrator and vertical gap absorber is illustrated in Fig. 1. The device is principally composed of top arched transparent glass, cylindrical concentrator, vertical gap, absorbent cloth (polyester fiber) and freshwater trough. With the simple but effective structure, it can be used for a large number of horizontal splicing to increase floating stability and realize large-scale seawater desalination. The schematic diagram of the system is shown in Fig. 2. The sunlight passes through the top arched transparent glass and will be concentrated by the cylindrical concentrator to directly heat the seawater accumulated in the vertical gap filling in the absorbent cloth. The vapor generated in the gap goes upward to the condensation chamber. And then, some small water drops are formed due to the condensation by the top arched transparent glass at a lower temperature. The water drops flow slowly along the curved surface and drop into the freshwater trough. Particularly, the absorbent cloth in the vertical gap will always fill with seawater automatically because of the siphon effect of the absorbent cloth.
The vertical gap with microstructure has very little thermal inertia, which can make the temperature of seawater rise faster because of the heating of light. Based on that, the evaporation performance of the device can be significantly improved. The concentrator is installed in the sealed cavity to keep it as clean as possible, thus maintaining high concentrating efficiency.
Figure 1
Fig. 1. The structure of the solar distiller with cylindrical surface concentrator and vertical gap evaporator.
3. Structure design of concentrator and vertical gap
3.1. Selection of concentrator
For the solar distiller studied in this paper, the performance of the concentrator determines the efficiency of the whole system.
First of all, the selection of a concentrator convenient to splice plays a significant role to achieve large-scale seawater desalination. Therefore, triangular concentrator (TC), CPC and cylindrical concentrator (CC) are adopted and compared for optical efficiency. In these cases, the height and width of the central vertical gap remain consistent for comparison, which are set as 6 cm and 2 mm, respectively. In the process of selecting the TC, it is found that a large amount of light will be directly reflected and escape from the concentrator so that the concentrator cannot converge the light to the central vertical gap when the opening of the concentrator is large enough. Therefore, the opening of 90° and 40° for TC are selected for comparison. As for CPC, the width of both the exit of the light and gap is required to keep the same in 2 mm. However, considering a larger opening can receive more light but leads to an unwillingly narrow and long CPC structure, the opening can be enlarged by 40° during modeling. The structure of the concentrators is shown in Fig. 3.
Figure 3
Fig. 3. The schematic diagram of different types of concentrators (a: cylindrical concentrator (CC), r = 6 mm, b: triangular concentrator (TC), β = 40°, c: triangular concentrator (TC), β = 90°, d: compound parabolic concentrator (CPC), β = 40°).
The reception rate of the TC, CPC and CC with different light incidence angles are shown in Fig. 4. The results show that the reception rate of the triangular concentrator will be sharply reduced with the increase of incidence angle. Compared with CPC, the reception rate of the CC is slightly better and it is also easier to manufacture. Therefore, for matching the vertical gap evaporator, the CC has better concentrating performance and simpler processing technology, which can better meet the requirements of the distiller for the concentrator. Hence, the following optical simulation and analysis specially aim at CC.
Figure 4
Fig. 4. The variation of reception rate of triangular concentrator, CPC and cylindrical concentrator with different light incidence angles.
3.2 Initial size design of cylindrical concentrator
The radius of the cylindrical concentrator relates to the height of the vertical gap. Before the simulation, the water absorption of absorbent cloth (polyester fiber) should be studied. In the preliminary experiment, we found that the absorbent cloth could be quickly wetted more than 10 cm. The shorter transport distance of vapor in the vertical gap is useful to reduce heat loss. Based on that, the initial height of the vertical gap is suggested as shorter and possible. Combined with the result of preliminary experimental, the height of the vertical gap is initially determined as 6 cm. The variation of reception rate of the cylindrical concentrator with light incidence angles for different radius of cylindrical concentrator is compared in Fig. 5. It can be concluded that when the radius of the concentrator increases, the reception rate decreases faster with the increase of light incidence angle. Fortunately, based on the concentrator radius of 6 cm, the reception rate is always above 98% and has little correlation with the light incidence angle. Thus, the concentrator radius of 6 cm is a better choice at the vertical height of 6 cm.
Figure 5
Fig. 5. The variation of reception rate of the cylindrical concentrator with light incidence angles for different concentrator radius.
3.3 Size optimization of vertical gap
On the condition that the concentrator is 6 cm in radius with a combination of the vertical gap in the height of 6 cm, the reception rate of the concentrator is noticeably above 98% with regard to the light incidence angles from 0o to 45o. Furthermore, with the consideration of material saving, concentration ratio improvement and vapor transportation distance shorten as much as possible, the height of vertical gap need further optimized. The variation of reception rate of the cylindrical concentrator with light incidence angles for different heights of gap is compared in Fig. 6. The results indicate that though the light incidence angle increases to 45o, the reception rate can definitely attain 80% when the gap height exceeds 5 cm. Combined with the transportation distance of vapor and concentration efficiency, the gap height of 5 cm is the most appropriate for the cylindrical concentrator in the radius of 6 cm.
Figure 6
Fig. 6. The variation of reception rate of the cylindrical concentrator with light incidence angles for different heights of vertical gap.
3.4 Analysis of ray number independence
In the optical simulation, the number of lights entering the device is set to 100, 1000 and 10000 with the light incidence angles from 0° to 45°. The variation of reception rate of the cylindrical concentrator with light incidence angles for different incidence light numbers is compared in Fig. 7. It can be seen that the reception rate tends to be consistent when the number of incidence light reaches 1000 and 10000. From above analysis, it can be concluded that the reception rate of the concentrator converges when the number of simulated lights attains 1000.
Figure 7
Fig. 7. The variation of reception rate of the vertical gap with light incidence angles for different incidence light numbers.
4. Analysis of optical performance
4.1 Energy density analysis
In LightTools software, the surface source with the parameter of 20 cm × 20 cm and the direct light with the energy density of 1000 W/m2 are set to obtain the energy density cloud map on the reception surface. The bottom of the reception surface of the vertical gap serves as the origin in the energy density distribution map. It can be seen from Fig. 8 that the position of the peak value of energy density on the left side of the reception plane will gradually move down as the light incidence angle increases from 0°. Meanwhile, the peak value of energy density presents a decreasing trend. By comparison, the peak energy density on the right side will gradually move up oppositely. It can be also found that the value of peak energy density on the left reception surface has disappeared when the incidence angle reaches 50°, which demonstrates that the left side of the reception surface can receive light directly to some extent.
The variation curve of energy density on the whole reception surface with different heights of the gap under different incidence angles is displayed in Fig. 9. It can be observed that when the incidence angle is 0°, the peak energy density is as high as 17925 W/m2. With the increase of the light incidence angle, the peak position of the energy density on the reception surface gradually moves down. Meanwhile, the peak energy density performs a similar decreasing trend. Particularly, considering that the peak position approaches to the seawater surface at the bottom of the gap, the seawater accumulated in the vertical gap can be directly heated by the concentrated light from the concentrator effectively even at a low position.
Figure 9
Fig. 9. The variation of energy density on the whole reception surface with the height of the gap in different incidence angles.
4.2 Size optimization of vertical gap
Since determining the optimal structure and parameters of the concentrator and gap (r = 6 cm, h = 5 cm), it is of great necessity to assess the variation of solar altitude angle, light incidence angle and reception rate with time in typical geographical area. In order to obtain the light incidence angle during the whole day, geometric analysis is carried out as follows.
Figure 10 depicts the relationship among solar altitude angle (α), solar azimuth angle (γ) and light incidence angle (θ1). Among them, line MA represents the solar light, surface ABCD represents ground-piston, line MC is identified as the normal of ground-piston. The line AD is regarded as the north-south direction line while the line AB is the east-west direction line. The plane BCM represents the normal plane on the east-west line AB, and the line MB is the projection of the solar light on the normal plane BCM of the east-west direction line. The line MD is identified as the projection of the solar light on the plane ECD, which represents normal plane of the north-south direction.
When the device is placed in east-west direction, the geometric relation in Fig. 10 satisfies Eq. (1):
Since line \(\vec{BA}\) is in the same direction as the device, and the effective part of the solar light \(\vec{MA}\) to the device can be regarded as \(\vec{MB}\). Thus, the angle between \(\vec{MB}\) and the ground-piston can be regarded as the light incidence angle (θ1) in east-west direction
When the device is placed in north-south direction, the geometric relation in Fig. 10 satisfies Eq.
Since line \(\vec{DA}\) is in the same direction as the device, similarly the effective part of the solar light \(\vec{MA}\) to the device can be regarded as \(\vec{MD}\). Thus, the angle between \(\vec{MD}\) and the normal of the ground-piston can be regarded as the light incidence angle (θ2) in south-north direction.
According to the geometric relationship of the angles in the Fig. 10, the light incidence angle θ1 and θ2 can be calculated in Eq. (3) and Eq. (4), respectively.
4.3 Annual optical performance analysis
An area at 17° north latitude is selected as the typical operation location for the device, and the variation of solar altitude angle (α), solar azimuth angle (γ) and light incidence angle (θ1/θ2) with time from 6:30 to 17:30 in summer solstice, autumnal equinox and winter solstice are illustrated in Fig. 11, respectively. It can be seen that the reception rate can exceed 80% more than 10 hours, even 90% at least 8 hours at summer solstice when the device is placed in east-west direction. In autumnal equinox, there are more than 11 hours during the whole day when the reception rate can reach 90%. Particularly, the reception rate can reach 80% at least 5 hours and 70% at least 8 hours in winter solstice. Because the device is placed in the east-west direction, it will be able to achieve effective concentration throughout the year as long as the concentrator can effectively concentrate light in winter solstice in the northern hemisphere. Therefore, when the device is placed in east-west direction, it can achieve effective concentration all year round.
Figure 11
Fig. 11. Solar altitude angle, light incidence angle and reception rate varying with time in east-west direction (E-W) and south-north direction (S-N), respectively (a: summer solstice, b: autumnal equinox, c: winter solstice).
As depicted in Fig. 11, when the device is placed in south-north direction, the reception rate can exceed 80% for more than 6 hours, which exceeds 90% at least 4 hours during the day of summer solstice. In autumnal equinox, there are more than 6 hours with the reception rate larger than 80% and 3 hours with the reception rate larger than 90%. Besides, the reception rate can reach 80% at least 5 hours and 70% at least 6 hours in the winter solstice.
It is suggested that when the concentrator operates in the regions within 17° north latitude, placing the concentrator in east-west direction is the better choice for a larger reception rate.
5. Energy analysis and theoretical water production calculation
5.1 Energy analysis of the system parts
In order to theoretically predict the water production performance and solar energy utilization efficiency of the solar distiller, energy balance is carried out to provide a basis to theoretical analysis.
The energy flow in the system is depicted in Fig. 12. The temperatures of important locations in the device and coefficients of convective heat transfer are shown and can be referred in the nomenclature table. Arrows in the diagram represent the direction of energy transmission.
In order to simplify the calculation process, some reasonable assumptions are made as follows:
- The surface of the concentrator in contact with the seawater is assumed as adiabatic.
- The temperature of all parts of the system is assumed as uniform
Based on heat transfer relationships, the energy balance analysis of each part of the system is carried out as follows:
-
Total energy entering the system
The total energy entering the system can be obtained as Eq. (5).
-
Energy analysis of the condensation cavity
Eq. (6) is given to express the energy transfer relationship for the condensation cavity.
\[ Q_{cv,3,4}+Q_{cv,2,4}+Q_{cv,4,5}=c_{p,4}\rho_4v_4\frac{{dT}_4}{d\tau} \]Qcv,3,4 is defined as the convective heat flux between the air in the condensation cavity and the surface of the concentration cavity. Qcv,2,4 is defined as the convective heat flux between the air in the condensation cavity and the evaporation surface. And Qcv,4,5 is defined as the convective heat flux between the air in the condensation cavity and the surface of condensation cavity. They could be calculated by Eqs. (7), (8) and (9).
\[ Q_{cv,3,4}=A_2(T_3-T_4)h_3 \]\[ Q_{cv,2,4}=A_2\left(T_2-T_4\right)h_4 \] -
Energy analysis of the concentration cavity
Eq. (10) is given to express the energy transfer relationship for the internal energy change rate of the concentration cavity.
\[ Q_{si,2}+Q_{cv,2,3}-Q_{cv,3,4}+Q_{cd,2,3}=c_{p,3}\rho_3v_3\frac{{dT}_3}{d\tau} \]Qsi,2 is defined as the solar energy flux absorbed by the concentration cavity. Qcd,2,3 is the conduction heat transfer from the vertical gap to the concentration cavity. And Qcv,2,3 is defined as the convective heat flux between the air in the concentration cavity and the vertical gap.
\[ Q_{si,2}=I_dA_1\tau_1(1-\tau_2) \]\[ Q_{cv,2,3}=A_4(T_2-T_3)h_5 \]\[ Q_{cd,2,3}=\frac{{kA}_4\left(T_2-T_3\right)}{\delta} \] -
Energy analysis of the vertical gap
Eq. (14) is given to express the energy transfer relationship for the internal energy change rate of the vertical gap.
\[ Q_{si,3}+Q_{r,5,2}-Q_{cv,2,4}-Q_{cd,2,3}-Q_{cds}-Q_{cv,2,3}=c_{p,2}\rho_2v_2\frac{{dT}_2}{d\tau} \]Qsi,3 is defined as the solar energy flux absorbed by the vertical gap. Qr,5,2 is the radiation heat transfer between the surface of condensation cavity and the evaporation surface. And the heat produced by the evaporation of seawater is Qcds.
\[ Q_{si,3}=I_dA_1\tau_1\tau_2\rho \]\[ Q_{r,5,2}=\frac{\sigma\left(T_2^4-T_5^4\right)}{\frac{1-\varepsilon_1}{A_1\varepsilon_1}+\frac{1}{A_1F_{31}}+\frac{1-\varepsilon_2}{A_3\varepsilon_2}} \]\[ Q_{cd,2,3}=\frac{{kA}_4\left(T_2-T_3\right)}{\delta} \] -
Energy analysis of the surface of condensation cavity
Eq. (18) is given to express the energy transfer relationship for the surface of condensation cavity.
\[ {Q_{si,4}+Q}_{cds}+{Q_{cv,4,5}-Q_{cv,5,1}+Q}_{r,5,2}=c_{p,5}\rho_5v_5\frac{{dT}_5}{d\tau} \]Qsi,4 is defined as the solar energy flux absorbed by the surface of condensation cavity. Qcv,5,1 is defined as convective heat flux between the external environment and the surface of condensation cavity.
\[ Q_{si,4}=I_dA_1(1-\tau_1) \]\[ Q_{cv,5,1}=\frac{A_1\left(T_1-T_4\right)}{\frac{1}{\ h_1}+\frac{1}{h_5}} \] -
Experience formula of evaporation rate of seawater per unit area
The water production rate of the device can be approximately calculated referring to the formula of evaporation, condensation and water production rate between the two parallel plates. The vapor on the evaporation and condensation surfaces is assumed to be saturated, thus the empirical formula of evaporation rate per unit aperture solar collector area (Me) can be expressed as in Eq. (21).
\[ M_e=16.273\times{10}^{-3}\frac{h_4}{h_{fg}}\left(p_2-p_5\right) \] - According to the optical simulation results, the reception rate of the vertical absorber in the cylindrical concentrator is better than that in the triangular concentrator and CPC concentrator.
- When the radius of concentrator and the height of vertical gap is 6 cm and 5 cm respectively, 80% of the sunlight within 45° incidence angle can be captured by the seawater in the vertical gap.
- The device placed in the east-west direction possesses superior performance for the island within 17° north latitude.
- For the area within 17° north latitude, there are more than 10 hours and 5 hours with a larger than 80% reception rate in the summer solstice and winter solstice respectively. In the autumnal equinox, there are more than 11 hours with a larger than 90% reception rate.
- The stable evaporation rate per unit solar collector area increases gently from 0.12 g/(m2‧s) to 0.65 g/(m2‧s) when the solar irradiance increases from 500 W/m2 to 1000 W/m2.
- P. V. Kumar, A. Kumar, O. Prakash, A. K. Kaviti, Solar stills system design: a review, Renewable and Sustainable Energy Reviews 51 (2015) 153-181. https://doi.org/10.1016/j.rser.2015.04.103
- R. P. Goswami, B. S. Negi, H. K. Sehgal, G. D. Sootha, Optical designs and concentration characteristics of a linear Fresnel reflector solar concentrator with a triangular absorber, Solar Energy Materials 21 (1990) 237-251. https://doi.org/10.1016/0165-1633(90)90057-8
- V. K. Jebasingh, G. M. Herbert, A review of solar parabolic trough collector, Renewable and Sustainable Energy Reviews 54 (2016) 1085-1091. https://doi.org/10.1016/j.rser.2015.10.043
- B. Chaouchi, A. Zrelli, S. Gabsi, Desalination of brackish water by means of a parabolic solar concentrator, Desalination 217 (2007) 118-126. https://doi.org/10.1016/j.desal.2007.02.009
- Q. Wang, Z. Zhu, H. Zheng, Investigation of a floating solar desalination film, Desalination 447 (2018) 43-54. https://doi.org/10.1016/j.desal.2018.09.005
- X. Ma, H. Zheng, S. Liu, Optimization on a cylindrical Fresnel lens and its validation in a medium-temperature solar steam generation system, Renewable Energy 134 (2019) 1332-1343. https://doi.org/10.1016/j.renene.2018.08.075
- Y. P. Yadav, A. K. Yadav, N. Anwar, P. C. Earnest, B. Norton, An asymmetric line-axis compound parabolic concentrating single basin solar still 9 (1996) 737-740. https://doi.org/10.1016/0960-1481(96)88389-3
- X. Ma, H. Zheng, S. Liu, A Review on Solar Concentrators with Multi-surface and Multielement Combinations, Journal of Daylighting 6 (2019) 80-96. https://dx.doi.org/10.15627/jd.2019.9
- S. Liang, H. Zheng, D. Cui, X. Ma, Optical Characteristic Investigation on an Underwater Adjustable Focus Solar Concentrator with Single-Layer Membrane, Journal of Daylighting 6 (2019) 169-175. https://dx.doi.org/10.15627/jd.2019.15
- F. Liu, H. Zheng, R. Jin, X. Ma, Design of a Multi-Surface Solar Concentrator, Journal of Daylighting 6 (2019) 176-186. https://dx.doi.org/10.15627/jd.2019.16
- Q. Wang, S. Liang, Z. Zhu, G. Wu, Y. Su, H. Zheng, Performance of seawater-filling type planting system based on solar distillation process: Numerical and experimental investigation, Applied Energy 250 (2019) 1225-1234. https://doi.org/10.1016/j.apenergy.2019.05.048
- A. Shafieian, M. Khiadan, A. Nosrati, A review of latest developments, progress, and applications of heat pipe solar collectors, Renewable and Sustainable Energy Reviews 95 (2018) 273-304. https://doi.org/10.1016/j.rser.2018.07.014
- Z. Xu, L. Zhang, L. Zhao, Ban. L, B. Bhatia, C. Wang, K. L. Wilke, Y. Song, O. Labban, J. H. Lienhard, R. Wang, E. N. Wang, Ultrahigh-efficiency desalination via a thermally-localized multistage solar still, Energy and Environmental Science 13 (2020) 830-839. https://doi.org/10.1039/c9ee04122b
- Z. Moussa, S. Noureddine, M. Yacine, B. M. Mohmd, Simulation study of a capillary film solar still coupled with a conventional solar still in south Algeria, Energy Conversion and Management 85 (2014) 112-119. https://doi.org/10.1016/j.enconman.2014.05.062
- S. Ahmadvand, B. Abbasi, B. Azarfar, M. Elhashimi, X. Zhang, B. Abbasi, Looking Beyond Energy Efficiency: An Applied Review of Water Desalination Technologies and an Introduction to Capillary-Driven Desalination, Water 11 (2019) 696. https://doi.org/10.3390/w11040696
- Y. Ito, Y, Tanabe, J. Han, T. Fujita, T. Katsumi, M. Chen, Multifunctional Porous Graphene for High‐Efficiency Steam Generation by Heat Localization, Advanced Materials 27 (2015) 4302-4307. https://doi.org/10.1002/adma.201501832
- X. Zhang, Y. Liu, X. Wen, C. Li, X. Hu, Low-grade waste heat driven desalination with an open loop heat pipe, Energy 163 (2018) 221-228. https://doi.org/10.1016/j.energy.2018.08.121
- T. Peng, N. George, C. Song, W. Song, J. Wu, J. Zhu, G. Chen, T. Deng, Solar-driven interfacial evaporation, Nature Energy 3 (2018) 1031-1041. https://doi.org/10.1038/s41560-018-0260-7
- X. Zhang, W, Kan, H. Jiang, Y. Chen, T. Cheng, H. Jiang, X. Hu, Capillary-driven low grade heat desalination, Desalination 410 (2017) 10-18. https://doi.org/10.1016/j.desal.2017.01.034
- X. Wang, M. L. Hsieh, J. A. Bur, S. Y. Lin, S. Narayanan, Capillary-driven solar-thermal water desalination using a porous selective absorber, Materialstoday Energy 17 (2020) 100453. https://doi.org/10.1016/j.mtener.2020.100453
- Z. Zhu, H. Zheng, Q. Wang, M. Chen, Z. Li, B. Zhang, The study of a novel light concentration and direct heating solar distillation device embedded underground, Desalination 447 (2018) 102-119. https://doi.org/10.1016/j.desal.2018.08.021
5.2 Theoretical water production calculation
Under stable condition, the ambient temperature is defined invariably as: T1 = 298.15 K for a convenient evaluation. The simultaneous Eq. (6), (10), (14) and (18) can form closed equations to solve the values of T2, T3, T4 and T5. The variation of evaporation rate per unit aperture solar collector area and evaporation surface temperature under different solar irradiances are shown in Fig. 13.
Figure 13
Fig. 13. The variation of evaporation temperature and evaporation rate per unit aperture solar collector area with solar irradiance.
Illustrated in Fig. 13, the stable evaporation rate per unit aperture solar collector area increases gently from 0.12 g/ (m2‧s) to 0.65 g/(m2‧s) when the solar irradiance increases from 500 W/m2 to 1000 W/m2. And the evaporation surface temperature can reach 357K when the direct vertical solar irradiance is 800 W/m2.
6. Conclusions
In this paper, a new solar distiller with cylindrical surface concentrator and vertical gap evaporator which can float on ocean is proposed. Optical simulation is carried out to find the optimal radius of the cylindrical concentrator and the height of the vertical gap. The annual optical performance of the concentrator is analyzed for the region within 17° north latitude. Finally, the energy analysis and theoretical water production calculation are carried out. Some conclusions are obtained as follows.
Acknowledgment
This work is supported by the National Science Foundation of China (No.51976013).
Contributions
The simulation and writing work of this paper are completed by J. Zhao. The idea behind this work is provided by H. Z. and G. Wang. S. Liang and F. Liu help to check the viewpoints and language to improve the manuscript.
Declaration of competing interest
The authors report no conflicts of interests.
References
Copyright © 2021 The Author(s). Published by solarlits.com.
 HOME
HOME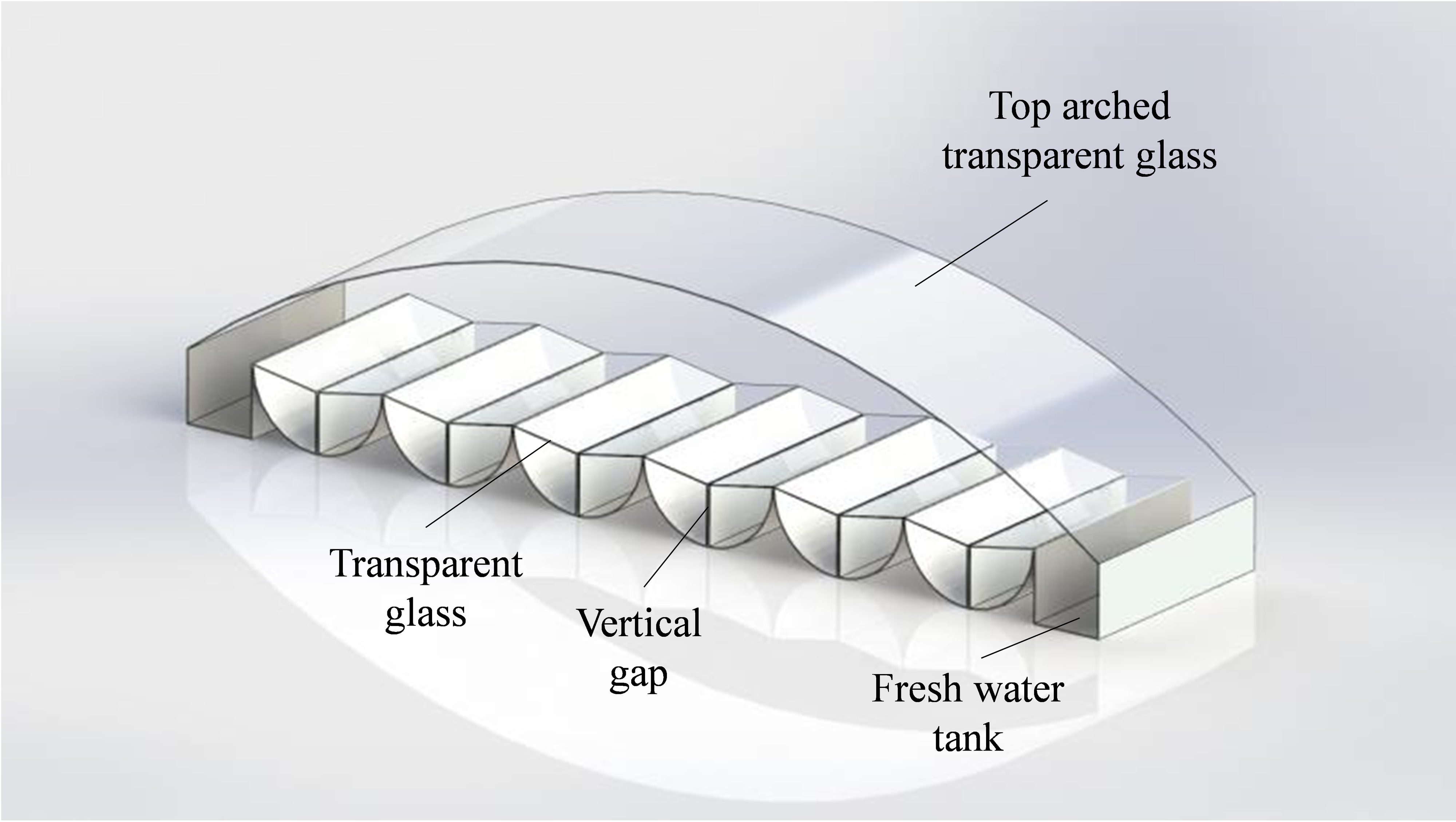 Figure 1
Figure 1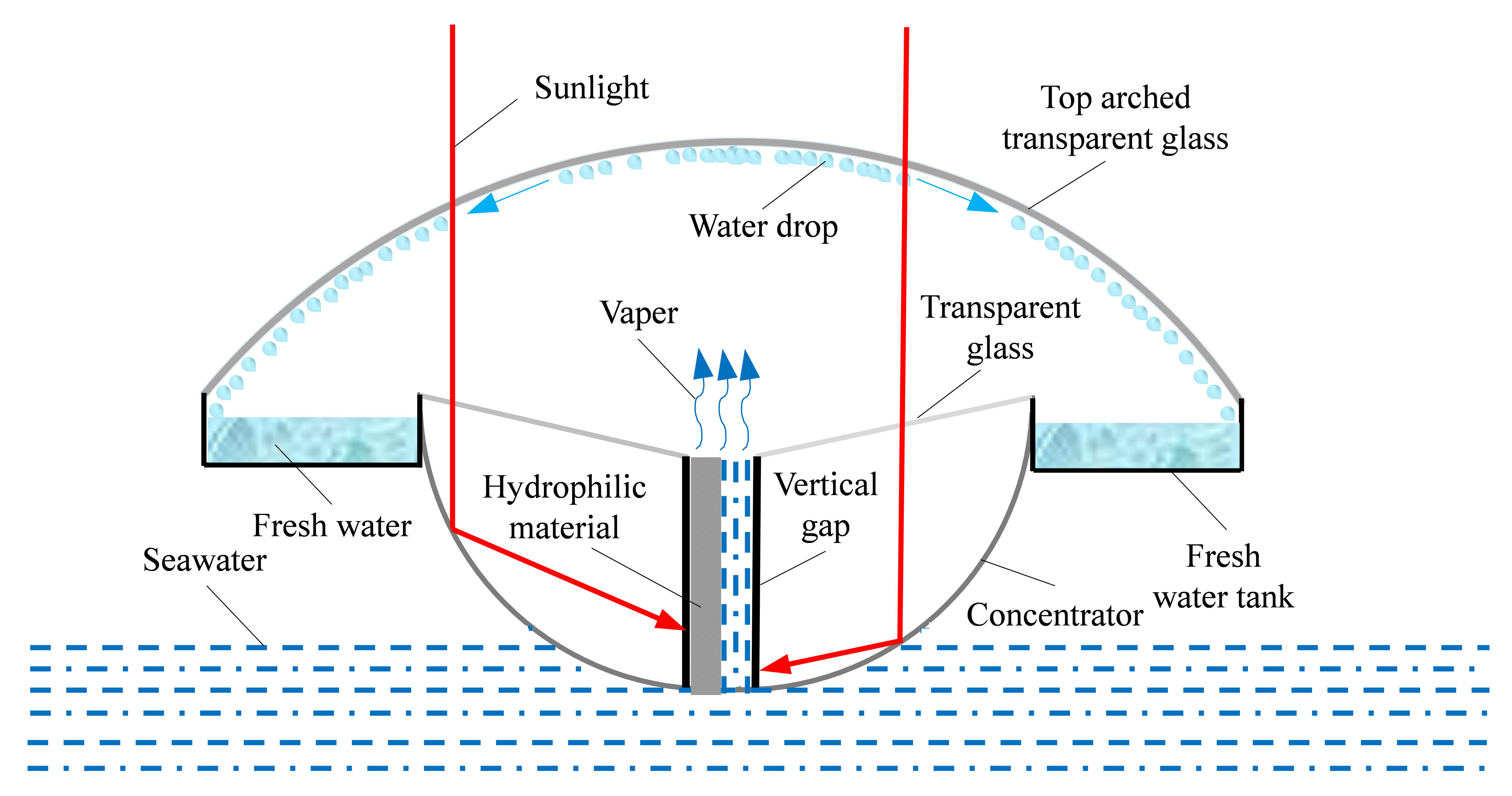 Figure 2
Figure 2 Figure 3
Figure 3 Figure 4
Figure 4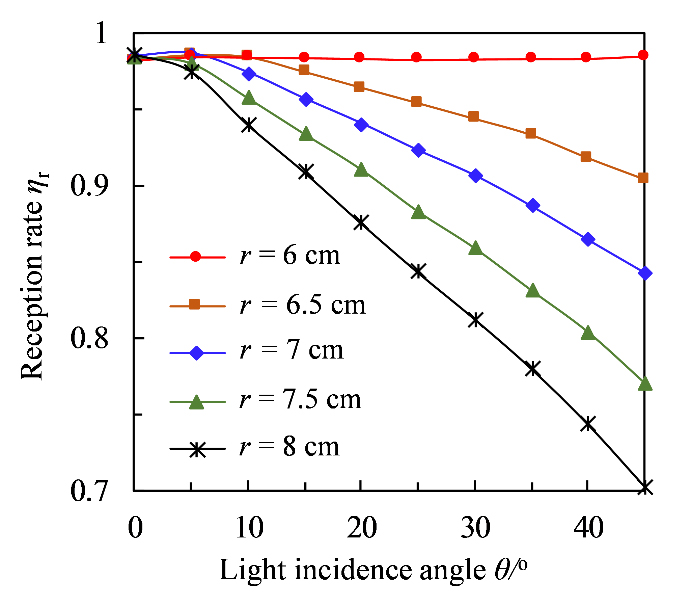 Figure 5
Figure 5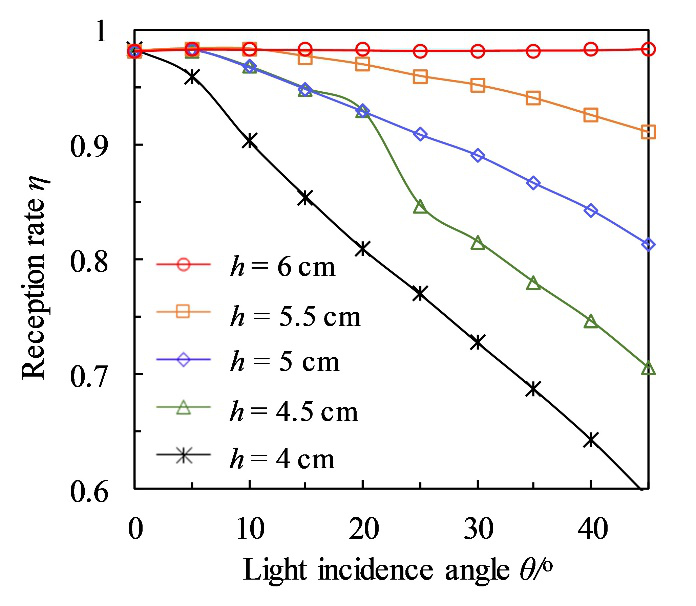 Figure 6
Figure 6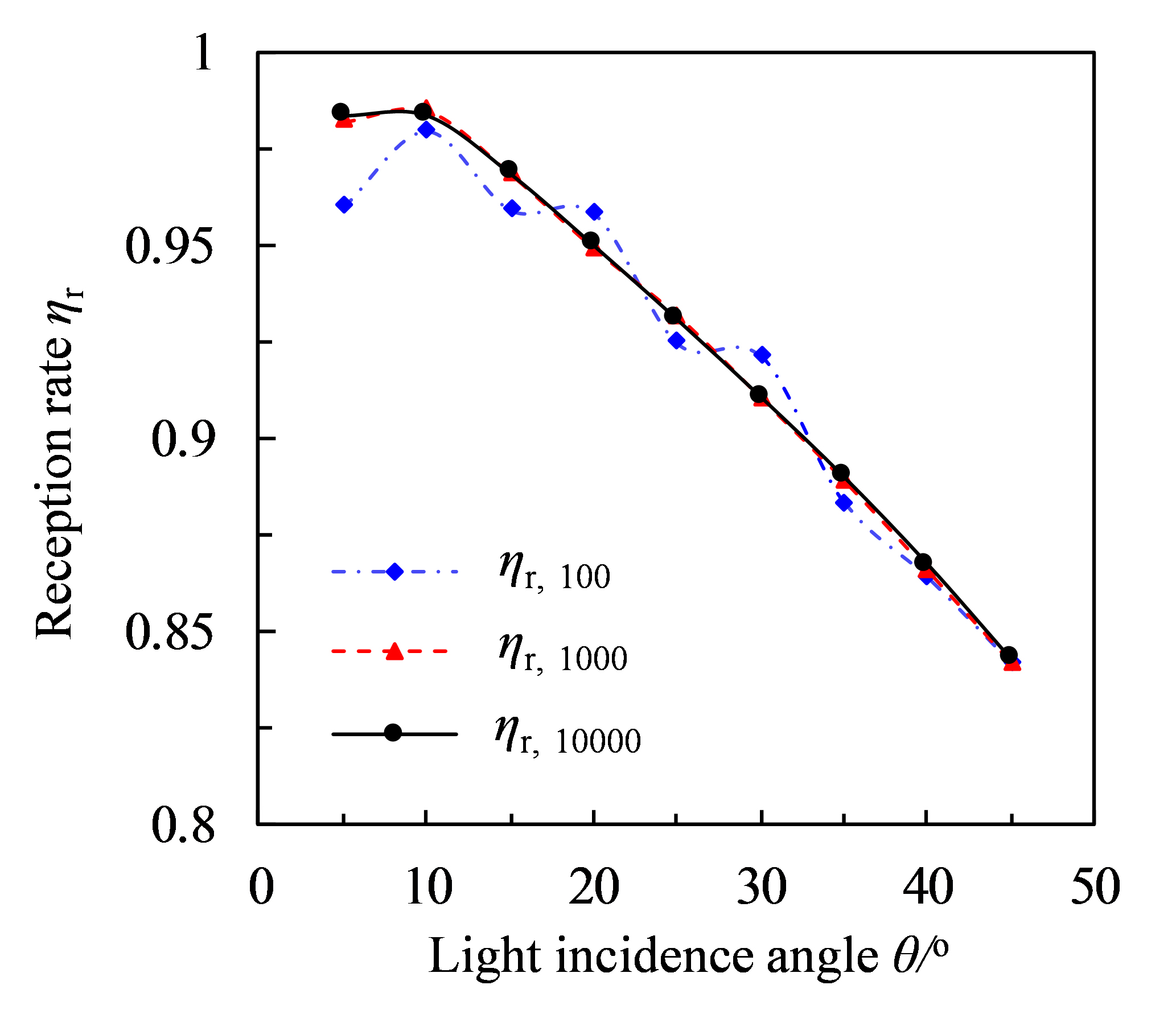 Figure 7
Figure 7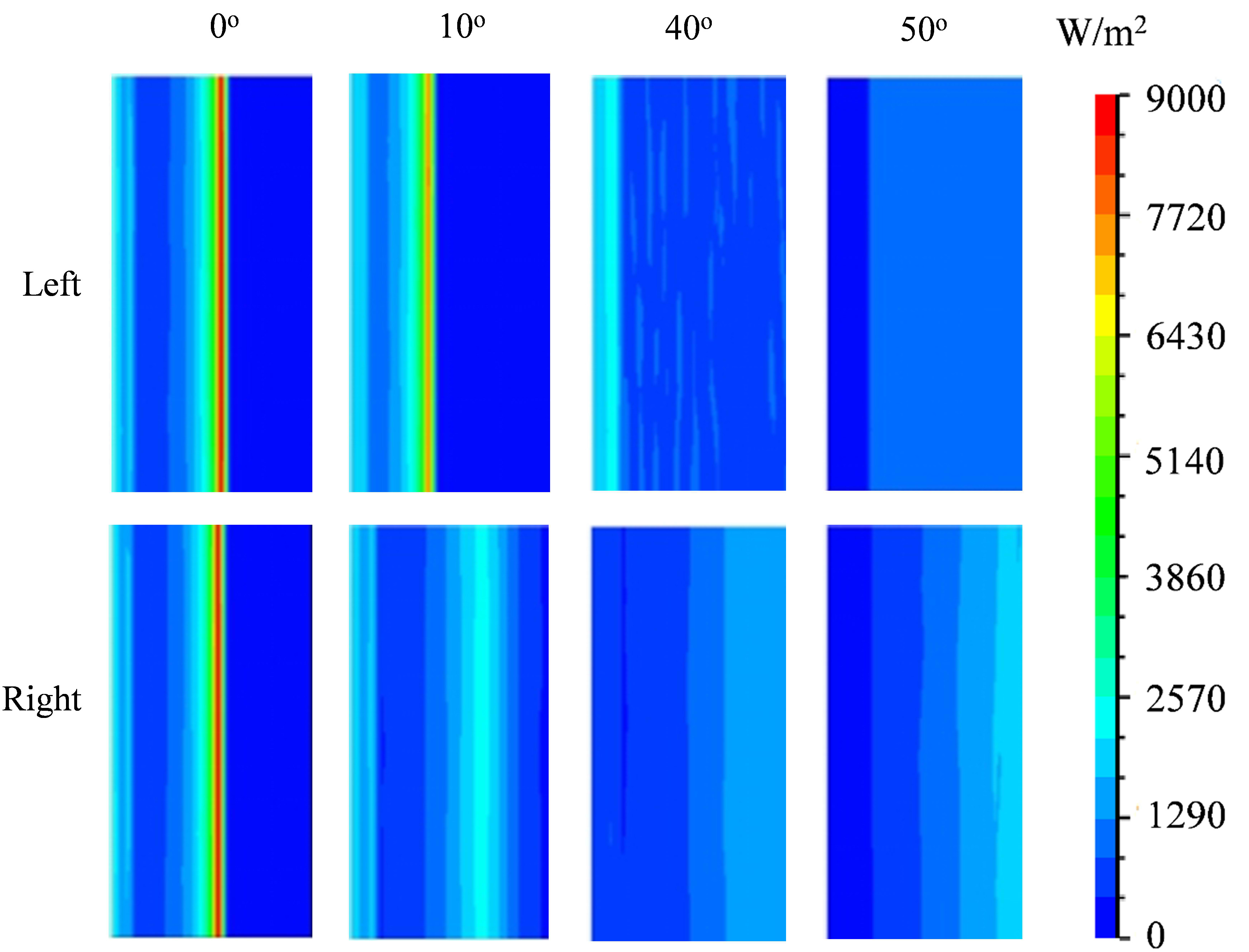 Figure 8
Figure 8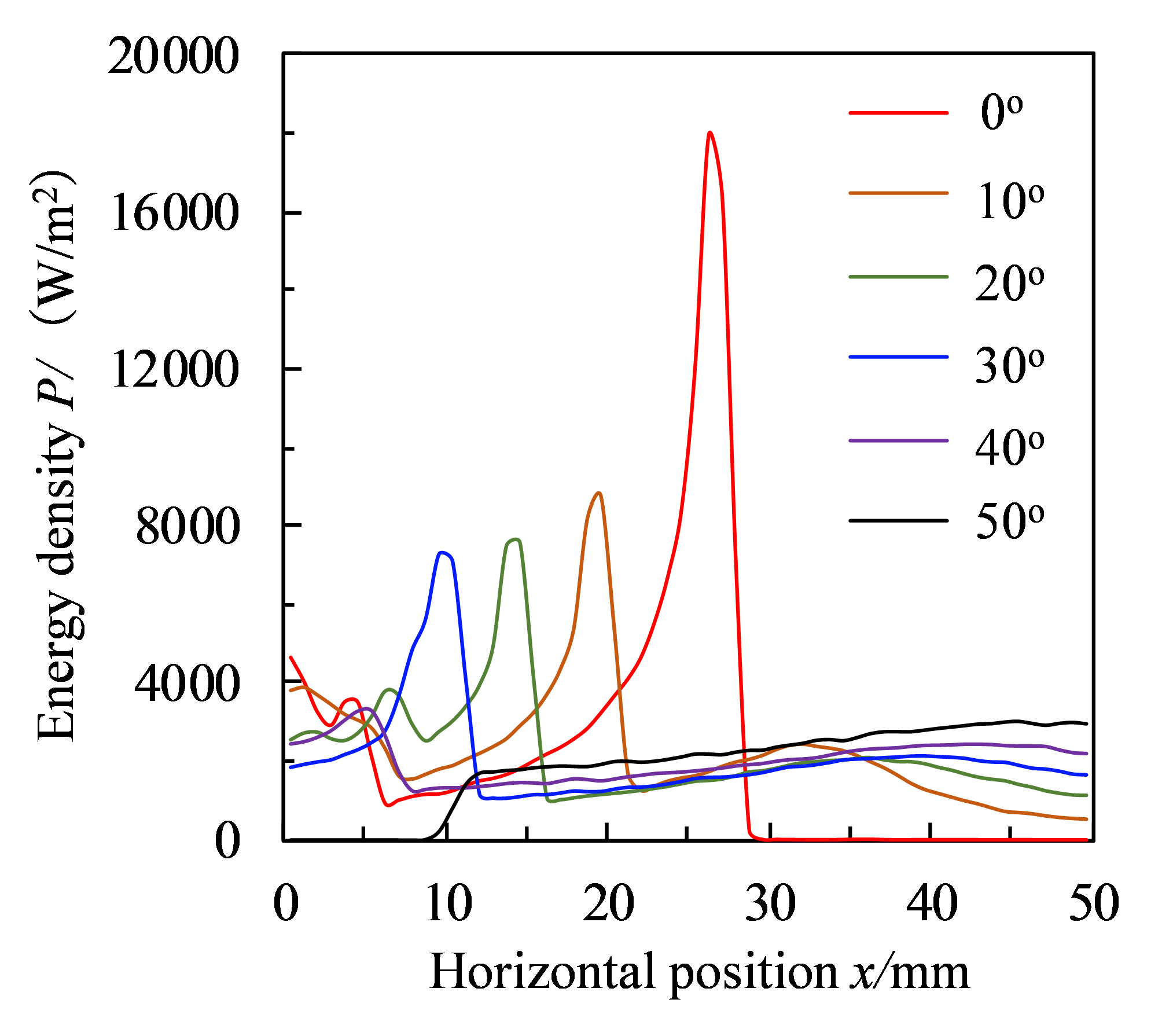 Figure 9
Figure 9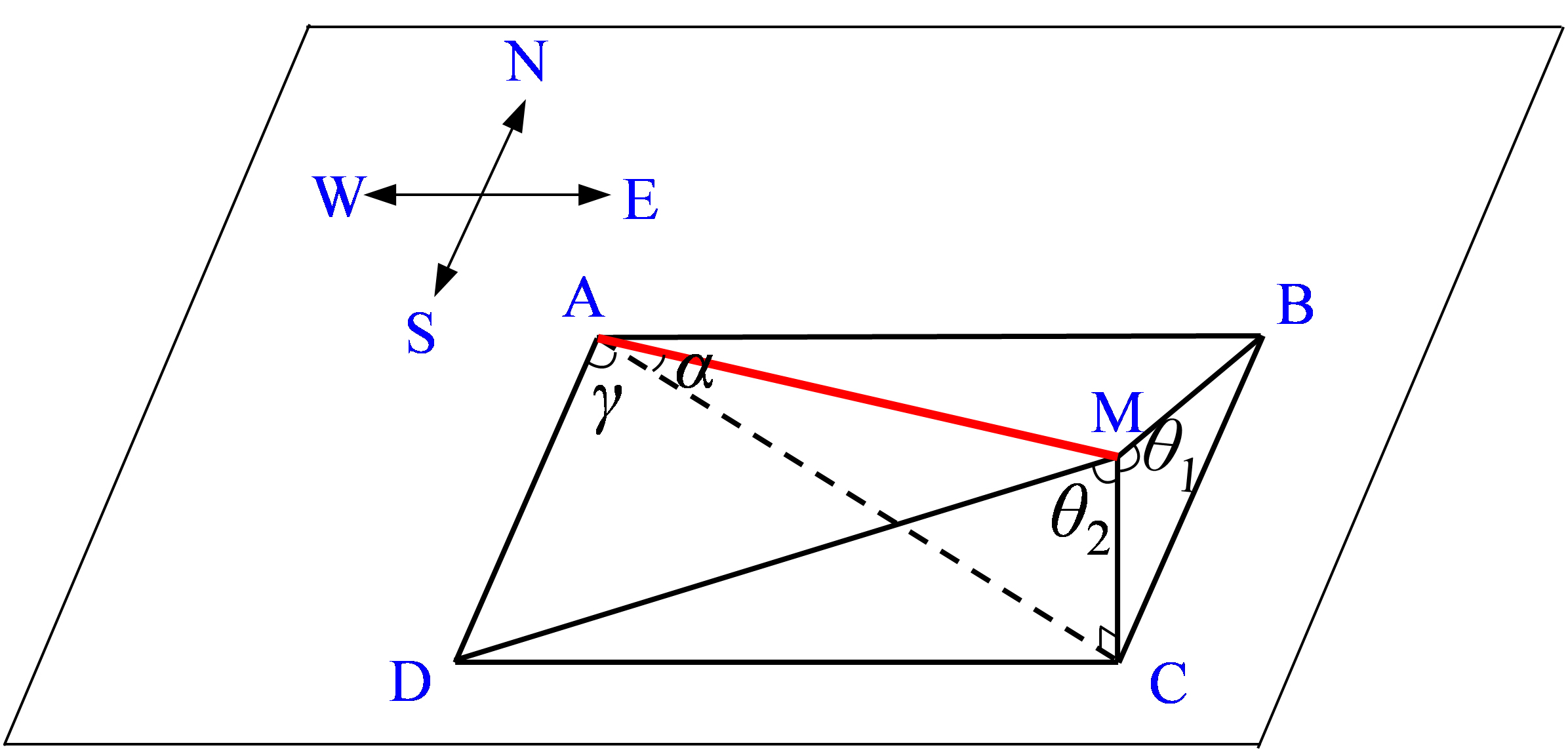 Figure 10
Figure 10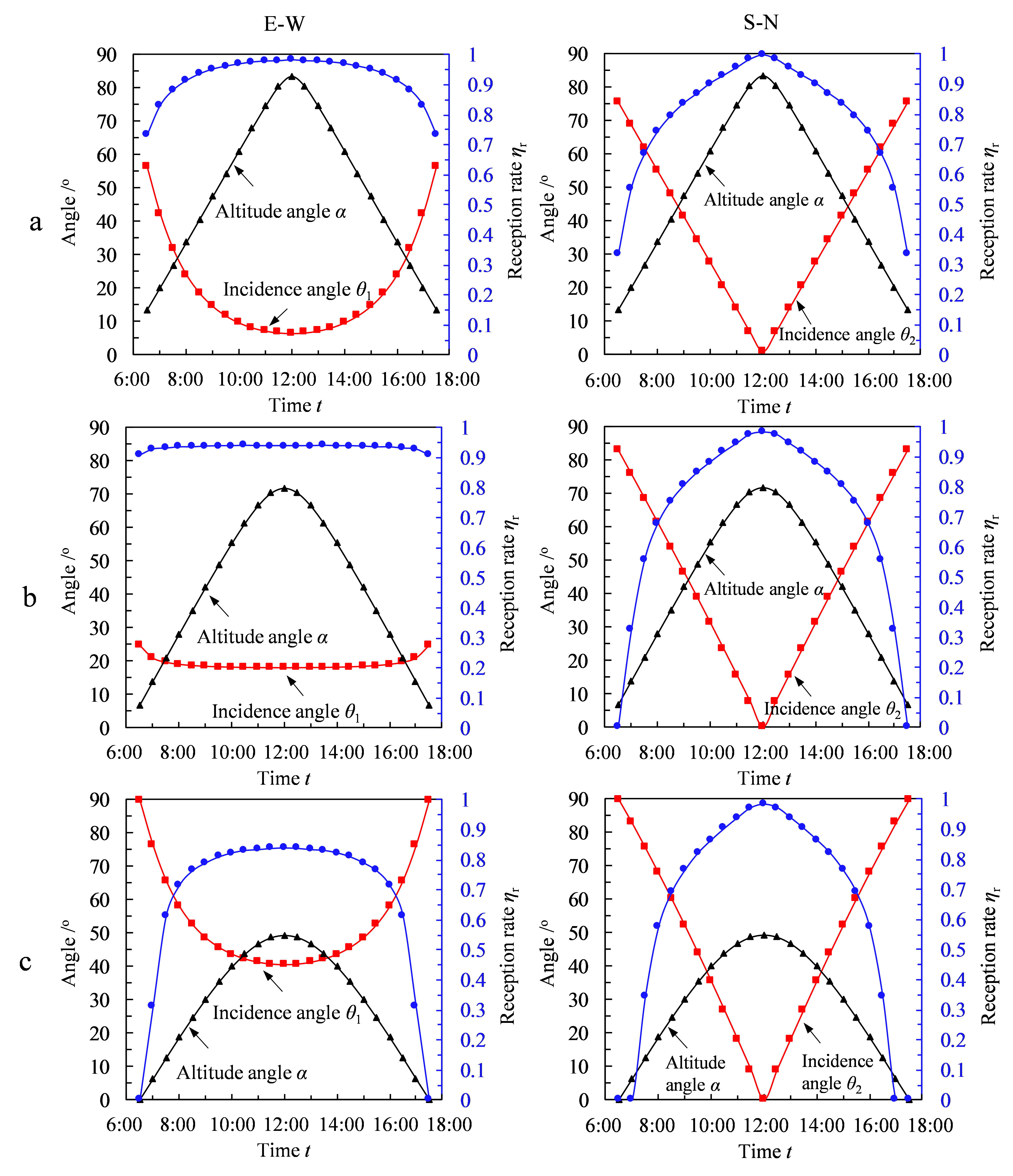 Figure 11
Figure 11 Figure 12
Figure 12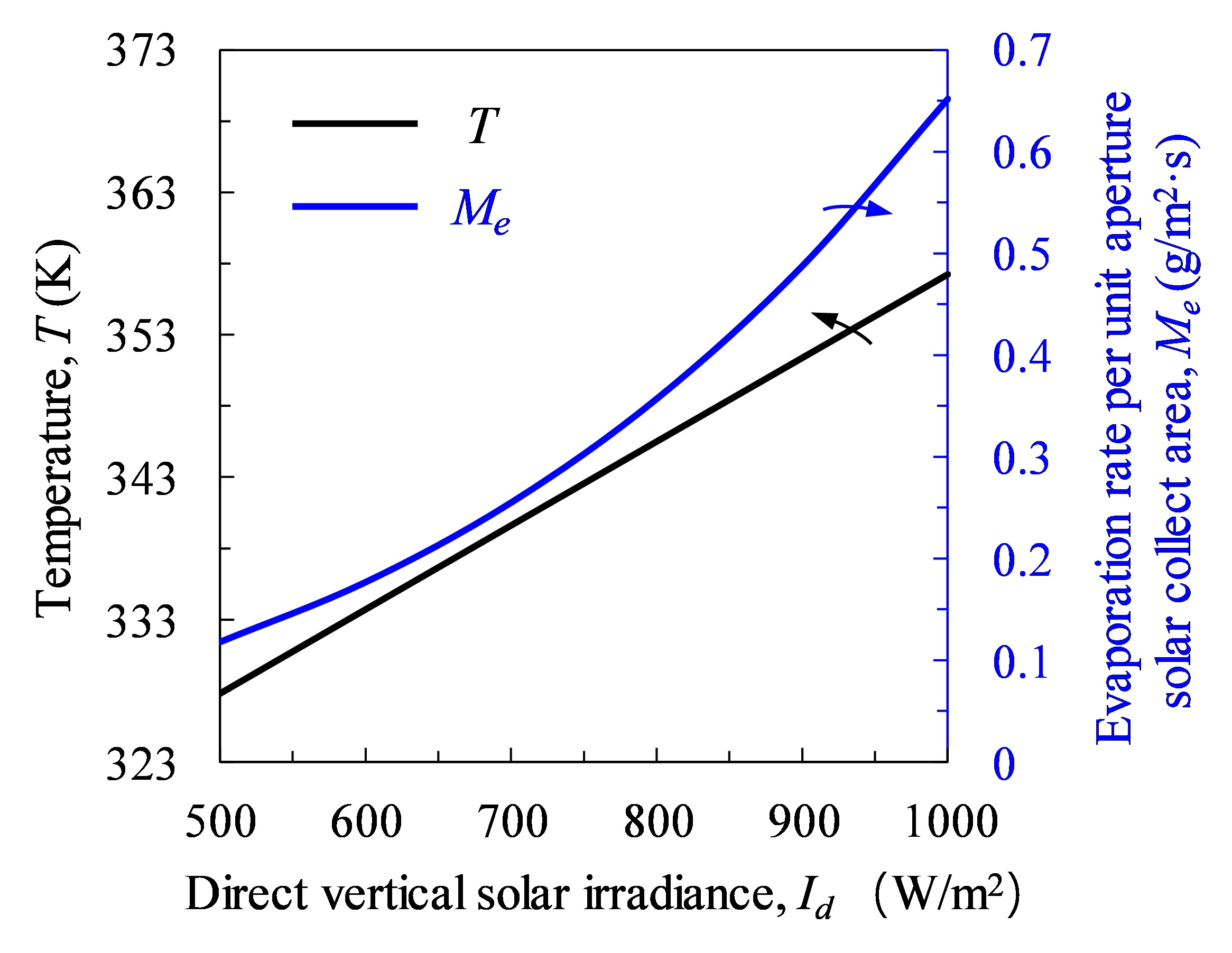 Figure 13
Figure 13


