Volume 9 Issue 2 pp. 257-265 • doi: 10.15627/jd.2022.19
Solar Angle Model for Daylight Redirection in Prismatic Panel
Mahshid Amani Zanganeh,a Iman Sheikh Ansarib,⁎
Author affiliations
a Faculty of Architecture and Urbanism, Islamic Azad University, North Tehran Branch, Tehran, Iran
b Faculty of Architecture and Urbanism, Art University of Isfahan, Isfahan, Iran
*Corresponding author.
mahshid.amani.z@gmail.com (M. A. Zanganeh)
ImanSheikhAnsari@gmail.com (I. S. Ansari)
History: Received 20 October 2022 | Revised 15 December 2022 | Accepted 19 December 2022 | Published online 27 December 2022
Copyright: © 2022 The Author(s). Published by solarlits.com. This is an open access article under the CC BY license (http://creativecommons.org/licenses/by/4.0/).
Citation: Mahshid Amani Zanganeh, Iman Sheikh Ansari, Solar Angle Model for Daylight Redirection in Prismatic Panel, Journal of Daylighting 9 (2022) 257-265. https://dx.doi.org/10.15627/jd.2022.19
Figures and tables
Abstract
An advanced complex fenestration system can utilize uniform daylight. Nonetheless, an inefficient design would increase solar heat gain and indoor temperatures, besides uneven light distribution that would cause the "cave effect." Prismatic panels are widely used as complex fenestration systems, providing uniform daylight. This paper proposes a computational model that integrates optical principles like Snell's law with environmental variables and visualizes the performance of prismatic panels in terms of redirection angle while encountering the prism refractive index and geometry at the specified geographic location. The proposed model entails a prismatic panel as a daylight system for redirecting daylight. In contrast to detailed modeling needed for simulation in software programs like Radiance, this computational tool provides a more straightforward and efficient solution for the initial design of light redirection panels that rely on the principle of refraction and evaluate their annual performance based on the angle of deviation. The model's applicability has been demonstrated by utilizing various triangular prism design examples with diverse materials in Frankfurt and Helsinki.
Keywords
Complex fenestration systems, Daylight redirection, Light guiding system, Computational model
Nomenclature
| BSDF | Bidirectional scattering distribution function |
| CFS | Complex fenestration systems |
| ROI | Return on Investment |
| N | Day of the year |
| CI | Local latitude |
| β | Surface tilt angle from the horizontal |
| ZS | Azimuth angle |
| h | Hour angle |
| A | Prism Angle |
| n | Prism Refractive Index |
| e | Prism Refracted Angle |
| i | Prism Incidence Angle |
| δ | Angle of Deviation |
1. Introduction
Daylighting is a significant indoor environmental concept that impacts comfort and residents' well-being [1-3]. Furthermore, it is known to be an effective energy-saving inactive method to harmonize and coordinate illuminance indoor living spaces where a high ROI can be expected [4-6]. A well-designed daylighting system can optimize solar radiations, reducing the winter's heating and summer's cooling energy consumption and lighting scheme. The daylighting system must be adjustable with the windows' direction, location configurations, and latitude [7,8].
Various passive and static shading techniques have been devised to enhance and balance sunlight in environments [9-14]. The static nature of these systems limits their performance, particularly in areas with mostly clear skies. On the other hand, dynamic sunlight redirection methods show substantially better performance [11]. Dynamic automated external shade devices reduce natural daylighting and, as a result, raise electric lighting demands when turned off [13].
Radiance® is a rendering and lighting simulation software that was developed at the Lawrence Berkeley National Laboratory (LBNL) [15-19]. Previous studies have shown its accuracy using the Integrated Environmental Solution [17] and [19] Radiance® uses backward raytracing technology to effectively handle indirect diffuse light and caustics [20-22]. However, due to advancements in light redirection materials, Radiance® may encounter new hurdles in its modeling due to its Monte-Carlo backward raytracing. At the same time, their specular nature makes them impossible to replicate using Radiance® [23,24]. On the other hand, Several studies illustrate that there are limitations in the selection (flexibility) of material types and geometry [25] due to challenges in daylight modeling.
This paper proposes a computational model based on optics laws to demonstrate the annual effect of sunlight redirection systems like the prismatic panel (Fig. 1) in hourly time steps with primary environmental variables like solar angle while encountering material optics nature, specifically refractive index, geometry, window direction, and latitude. Moreover, generating BSDF from the measured data for input to simulation tools could enhance daylight simulation software capabilities like Radiance®. However, the resolution of measured and tabulated BSDF data needs to match the optical properties of the represented system and the respective application. Higher resolution BSDF data is required for a prismatic panel with prominent peaks in the scattering distribution than a Lambertian, translucent panel [6].
2. Literature review
Mirror panels, prismatic or holographic glazing panels, and core daylighting systems such as light guides, light pipes, or Fresnel lenses linked with fiber optics improve daylighting access and connection to the outside; and express variations in illumination intensity over time for the area located deeper inside a building, or even below ground level. The high cost and space requirements for large-scale core daylighting systems are significant drawbacks. As a result, they are best suited for new structures and restricted retrofit applications when enough daylighting cannot be provided using the previously outlined methodologies [26]. Coplanar window films, shades, and between-pane daylight-redirecting devices have been developed as low-cost alternatives. These systems aid in illuminating a building's central areas by Edge windows receiving direct sunlight and/or diffuse skylight, which is redirected [27]. Since the early 1900s, glazing systems have advanced dramatically, ranging from double and triple-glazed panels to the production of CFS [28]. A window with prismatic panels that directs the light from the outside and throws it deep into the space has been used since 1897, and its exemplary utilization could be seen in Frank Lloyd Wright's design [28,29]. Generally, Prismatic panels are devices made of clear glass or acrylic materials that redirect or refract sunbeams [30].
Many researchers have demonstrated the prism's ability to redirect light [30]. A study conducted solstice-to-solstice field testing in an office testbed employing prismatic blinds, dual-zone mirrored blinds, transparent diffusing panels, and automated motorized blinds. According to the findings of this study, at a depth of 3.8m from a south-facing, large-area window, yearly lighting energy savings of 62-69 percent were feasible compared to a reference example with no lighting controls [31]. The viability of generating affordable scalable coatings made from redox-active organometallic polymers and self-assembled colloidal crystals were tested with electro-actuated metamaterial coatings in a lab setting. If implemented, this was reported to offer potential annual lighting energy savings [32]. In proposing daylighting and energy analysis, multi-sectional facades with prismatic panels on the upper side of windows have been examined [33]. Sabry, M examined the low-latitude possibilities of a Prismatic total internal reflection low-concentration photovoltaics-integrated façade. In another experimental study [34], a high-potential prismatic glazing application in building curtain walling facades was released to improve space heating and cooling while offering natural daylighting. Another examination proposed an experimental exploration of the redirection of sunlight in terms of efficient micro-optics [10]. Another extensive study compared four prismatic glass façade options [7]. The study results illustrated that Triple glazing with a reverse symmetrical rectangular prism has been more effective than blocking direct summer radiation while allowing solar heat to pass through during winter. Dogan and Stec studied the possibilities of a dynamic dual-axis daylight redirection prototype to increase daylight availability while decreasing lighting energy usage [35].
The combination of automatic reflective slats and prismatic panels, which may spread daylight across the ceiling and offer steady light, has been presented in a study [1]. A new study controls the louver tile of a dynamic micro prism foil louver according to different sun incident angles to optimize work plane illuminance in deep offices' central/rear zone analyzed based on simulations[36]. The results revealed that the Automated prismatic louver system provides adequate daylight distribution, saving electrical energy [37]. Table 1 represents selected literature that focuses on prismatic panels and simulations.
Table 1
Table 1. A summary of the selected literature with a focus on prismatic panel and simulations.
While numerous computational simulation tools analyze the behavior of prismatic panels in the building, most of these tools are either complex in modeling and simulation or not comprehensive in analyzing prismatic panels [38] that, causing limited flexibility in choosing materials, location and shape. Therefore, this paper proposes a computational model that integrates optics principles like Snell's law with environmental variables and visualizes the performance of prismatic panels in terms of redirection angle while encountering the prism refractive index and geometry at the specified geographic location.
3. Background
3.1. Solar angles
The location of the sun in the sky at a specific time of day and year must be predicted with some degree of accuracy for most solar applications. Besides, the earth's axis of rotation (the polar axis) is inclined at a 23.45-degree angle to the ecliptic axis, which is normal to the ecliptic plane [39]. In other words, the solar altitude angle is between the sun's rays and a horizontal plane, and the solar azimuth angle, z, is the angle of the sun's rays measured in the horizontal plane from true south in the Northern Hemisphere or due north in the Southern Hemisphere (Fig. 2). Therefore, the following is the general expression for the solar incidence angle, θ, which is the angle between the sun's rays and the normal surface [40].
3.2. Optical behavior of a prism
When a light beam traveling in a transparent medium collides with another transparent medium, a portion of the light is reflected from the first medium while the remainder enters the second. The propagation direction of an obliquely incident beam of light that enters the other medium changes. This is known as light refraction, allowing the prismatic panel to divert the sunbeam into the depths of space. Snell discovered the following refraction laws experimentally [41]:
- At the point of incidence, the incident ray, the refracted ray, and the normal to the interface are all in the same plane.
- The sine of the angle of incidence to the angle of refraction ratio is constant.
The mathematical expression of refraction through a triangular prism is represented in the path of light through a triangular prism ABC is seen in Fig. 3. the angles of incidence and refraction at the first face ab are i and r1, respectively, whereas the angle of incidence (from glass to air) and the angle of refraction or emergence at the second face ac are r2 and e, respectively. The angle of deviation, δ, denotes the angle formed by the emerging ray RS and the direction of the incident beam PQ. Applying Snell's law to each of the two refracting surfaces, where is the refractive index of the prism, would result:
4. Method
The primary goal of the prismatic panel is to redirect sunlight upwards. The objective of the panel in a window system is to reduce direct solar radiation during the summer by dispersing and diverting sunlight upwards, improving the homogeneity of daylighting inside the area, and redirecting daylight to the depth of space (Fig. 4). The proposed model aims to calculate the refraction angle of a prismatic form with specified geometry and material that diverts incident light from various solar latitudes.
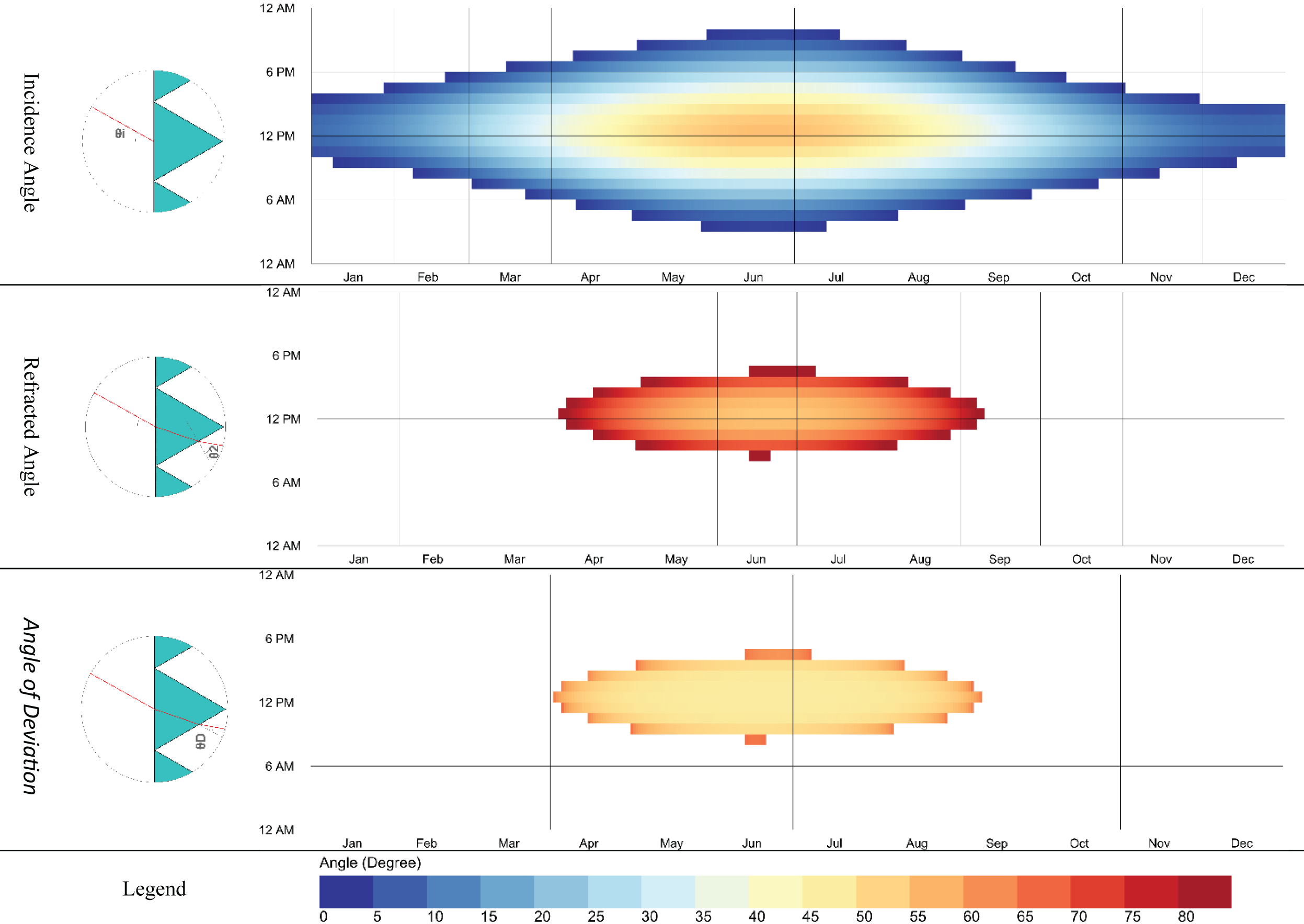
In order to determine inputs for the computational model, at first, the solar altitude angle is calculated annually for an hourly time step at any given location using local latitude and a solar azimuth (related to the prismatic panel installed window orientation) (Fig. 5). At the end of this step, the angle between the sunbeam and prism face normal is determined. Secondly, the prism incidence angle is compared to the prism's critical angle to filter the inputs for agile calculation. Finally, the model will determine the refracted angle of the prismatic panel by applying the Snell law and calculating refraction. In conclusion, the angle of deviation formed by the emerging ray through refraction and the direction of the incident ray is the focus of this study to represent the performance of the prismatic panel.
Figure 6 shows the incidence, refracted angles and deviation angles of the polycarbonate prismatic panel facing south in Helsinki (60.17° N); This is the instance where the solar incidence angle and the angle between the sun ray and the prism face normal are the same due to the rotation of prisms. The steps below show that by applying the primary physics principle described in the background section, the computational model could represent the annual performance of prismatic panels.
Figure 6
Fig. 6. Steps of a proposed computational model in prismatic panel facing south (latitude: 60.17° N).
5. Results
In order to demonstrate various applications of the proposed model, the following cases have been evaluated and visualized. Frankfurt (50.11° N) and Helsinki (60.17° N) were chosen primarily to show how the latitude would affect the prism performance. Figure 7 shows the prism result with an angle of 60° (equilateral triangle) and a refractive index of 1.49 (acrylic (PMMA)) facing the true south. The relationship between solar altitudes and prism performance in deviation of the incidence angle is directly related to the critical angle of the prismatic panel. Moreover, the maximum deviation angle is also related to the critical angle, and in both locations is 56.11° because this parameter is related to prism material. As it is represented, using a prismatic panel at a high altitude would result in the total internal reflection in the winter. Therefore, efforts to redirect daylight to deeper space would be adverse; as presented in the figure below, the prismatic panel redirects beam inside space for less than half the time when the sunbeam reaches the window in Helsinki. Furthermore, because the angle of deviation is limited due to the material redirecting the beam, it would not improve the room's daylight, even in the summer, and would only illuminate the ceiling near the window.
Furthermore, the material refractive index in most daylight simulations is neglected because of challenges in modeling the BSDF, and most simulated cases use backward ray tracing, limiting the refractive effect. Besides, the effect of critical angle is inevitable, as mentioned above, so the effects of prism materials (refractive index) have been presented in Fig. 8, considering all the parameters mentioned above. The refractive index of window glass, acrylic (PMMA), and polycarbonate (PC) are retrieved from [42], and their values are 1.52, 1.49, and 1.59, and the maximum deviation angle is 57.78, 56.11, and 63.85, respectively. Since changing the material, the critical angle is changing, and the number of hours’ prismatic panels refract sunbeam is also changing in the same location. Further, when the prismatic panel gets evaluated, the time of year that prismatic panels work effectively is also an essential criterion. Optimization based solely on the summer or winter solstices would not result in a practical design. The upward redirection or higher angle of deviation should be incorporated with a reflective ceiling for well-illuminated space.
The prism angles of 60°, 45°, and 30° have been studied, and the effect of prism geometry is represented in Fig. 9, assuming the acrylic (PMMA) prism faced true south in Helsinki. The effect of geometry and the angle of the prism is apparent. While the prism with a top angle of 30° represents the limited performance in deviation angle, the extent of the time of the year is more promising. Overall, the prism geometry has a high impact on deviation angle, and in its design processes, the room's interior and occupant position in space should be considered. As represented, the geometry of the prism is the most influential parameter regarding the annual performance.
6. Conclusions
The findings suggest that prismatic structures can be used in modern façade envelopes as a low-cost alternative to other daylight systems, and the prismatic panel improves daylight distribution inside the space and the daylight levels in deep spaces. However, its function is very limited to the material, and its geometry and improper design would adversely affect daylight illumination. This paper presents a simplistic computational model that uses optics concepts with environmental variables to evaluate prismatic panels' initial design considering material and geometry in the case of Deviation Angle. The advantage of the proposed model is the agile evaluation of the performance of the prismatic panel annually with hourly time steps.
The most influential parameter is the prism angle since it is directly related to the critical angle that limits the function of the prism even if the material remains the same. In general, an equilateral triangle represents optimized performance, and as the shape of the prism becomes more acute, the lower performance can be seen. The other variable that impacts the critical angle of the prism is material. Materials' effect on prism performance is the degree of deviation and time during the year. In case of deviation, the materials with a higher refractive index perform better but are limited to the applicable time of the whole year. These effects could be inferred more simply in the annual time frame, as shown in the results section that assists the designer in making a holistic decision regarding all aspects of the prism and not focusing on a specific time of the year for evaluation or specific material properties or geometry due to challenges of modeling software.
The focus of the proposed model was on the triangular prismatic panel since their wide use; however, the quadrilateral geometry could be the focus of future papers. Moreover, this paper focuses on beam redirection, and the dispersion of light by prisms is not considered in the modeling. This effect is neglected in most papers, primarily research focused on raytracing. Overall, to achieve the best daylight performance by the prism, detailed modeling is needed for cases like the occupant's location in space so that the deviation of the sunbeam does not cause glare.
Contributions
All the authors contributed equally.
Declaration of competing interest
The authors declare no conflict of interest.
References
- A. Eltaweel, M. Alaa Mandour, Q. Lv, Y. Su, Daylight distribution improvement using automated prismatic louvre, Journal of Daylighting 7 (2020) 84-92. https://doi.org/10.15627/jd.2020.7
- M. Alva, A. Vlachokostas, and N. Madamopoulos, Experimental demonstration and performance evaluation of a complex fenestration system for daylighting and thermal harvesting, Solar Energy 197 (2020) 385-395. https://doi.org/10.1016/j.solener.2020.01.012
- T.E.Kuhn, State of the art of advanced solar control devices for buildings, Solar Energy 154 (2017) 112-133. https://doi.org/10.1016/j.solener.2016.12.044
- A.Vlachokostas, and N. Madamopoulos, Daylight and thermal harvesting performance evaluation of a liquid filled prismatic façade using the Radiance five-phase method and EnergyPlus, Building and Environment 126 (2017) 396-409. https://doi.org/10.1016/j.buildenv.2017.10.017
- A.Lin, and J. Phillips, Optimization of random diffraction gratings in thin-film solar cells using genetic algorithms, Solar Energy Materials and Solar Cells 92 (2008) 1689-1696. https://doi.org/10.1016/j.solmat.2008.07.021
- A.McNeil, E.S. Lee, and J.C. Jonsson, Daylight performance of a microstructured prismatic window film in deep open plan offices, Building and Environment 113 (2017) 280-297. https://doi.org/10.1016/j.buildenv.2016.07.019
- I.A.Mashaly, et al., A prismatic daylight redirecting fenestration system for southern skies, Renewable Energy 109 (2017) 202-212. https://doi.org/10.1016/j.renene.2017.02.048
- C.E. Ochoa, et al., Considerations on design optimization criteria for windows providing low energy consumption and high visual comfort, Applied energy 95 (2012) 238-245. https://doi.org/10.1016/j.apenergy.2012.02.042
- S. Klammt, A. Neyer, and H.F. Müller, Redirection of sunlight by microstructured components-Simulation, fabrication and experimental results, Solar Energy 86 (2012) 1660-1666. https://doi.org/10.1016/j.solener.2012.02.034
- S. Klammt, A. Neyer, and H.F. Müller, Microoptics for efficient redirection of sunlight. Applied optics 51 (2012) 2051-2056. https://doi.org/10.1364/AO.51.002051
- B. Raphael, Active control of daylighting features in buildings. Computer‐Aided Civil and Infrastructure Engineering 26 (2011) 393-405. https://doi.org/10.1111/j.1467-8667.2010.00692.x
- I.A.Mashaly, K. Nassar, and S. El-Haggar, Mathematical model for designing a light redirecting prismatic panel, Solar Energy 159 (2018) 638-649. https://doi.org/10.1016/j.solener.2017.11.014
- M. Liu, K.B. Wittchen, and P.K. Heiselberg, Control strategies for intelligent glazed façade and their influence on energy and comfort performance of office buildings in Denmark. Applied Energy 145 (2015) 43-51. https://doi.org/10.1016/j.apenergy.2015.02.003
- Vlachokostas, A. and N. Madamopoulos, Liquid filled prismatic louver façade for enhanced daylighting in high-rise commercial buildings, Optics Express 23 (2015) A805-A818. https://doi.org/10.1364/OE.23.00A805
- G. J. Ward, The RADIANCE lighting simulation and rendering system, in: Proceedings of the 21st annual conference on Computer graphics and interactive techniques, 1994. https://doi.org/10.1145/192161.192286
- G. Ward, and R. Shakespeare, Rendering with Radiance: the art and science of lighting visualization, 1998.
- C.F. Reinhart, and O. Walkenhorst, Validation of dynamic RADIANCE-based daylight simulations for a test office with external blinds, Energy and buildings 33 (2001) 683-697. https://doi.org/10.1016/S0378-7788(01)00058-5
- I. Edmonds, and D. Pearce, Enhancement of crop illuminance in high latitude greenhouses with laser-cut panel glazing, Solar Energy 66 (1999) 255-265. https://doi.org/10.1016/S0038-092X(99)00030-4
- S.M. Mousavi, T.H. Khan, and Y.-W. Lim, Empirical validation of Radiance-IES daylight simulation for furnished and unfurnished rooms under a tropical sky, International Journal of Sustainable Building Technology and Urban Development 7 (2016) 61-69. https://doi.org/10.1080/2093761X.2016.1167646
- J. Mardaljevic, Daylight simulation: validation, sky models and daylight coefficients,De Montfort University Leicester, 1999.
- A.Vlachokostas, C. Volkmann, and N. Madamopoulos, Prismatic louver active façades for natural illumination and thermal energy gain in high-rise and commercial buildings. in: International Conference on Photonics Solutions, 2013, SPIE. https://doi.org/10.1117/12.2022026
- R. Labib, Improving daylighting in existing classrooms using laser cut panels, Lighting Research & Technology 45 (2013) 585-598. https://doi.org/10.1177/1477153512471366
- A. Tabadkani, A. Roetzel, H. Xian Li, A. Tsangrassoulis, Daylight in Buildings and Visual Comfort Evaluation: The Advantages and Limitations, Journal of Daylighting 8 (2021) 181-203. https://doi.org/10.15627/jd.2021.16
- P. Apian-Bennewitz, J. de Boer, B. Bueno, B. Deroisy, Y. Fang, D. Geisler-Moroder, L.O. Grobe, J.C. Jonsson, E.S. Lee, Z. Tian, T. Wang, G.J. Ward, H. Wilson Y. Wu, Analysis and evaluation of BSDF characterization of daylighting system, D. Geisler-Moroder, Ed., IEA SHC, 2021. https://doi.org/10.18777/ieashc-task61-2021-0012
- E. Brembilla,and J. Mardaljevic, Climate-Based Daylight Modelling for compliance verification: Benchmarking multiple state-of-the-art methods, Building and Environment 158 (2019) 151-164. https://doi.org/10.1016/j.buildenv.2019.04.051
- M. Ayoub, 100 Years of daylighting: A chronological review of daylight prediction and calculation methods, Solar Energy 194 (2019) 360-390. https://doi.org/10.1016/j.solener.2019.10.072
- S.F. Haeringer, et al., Design and experimental proof-of-concept of a façade-integrated Solar Thermal Venetian Blind with heat pipes. Journal of Facade Design and Engineering, (2020) 131-156.
- D. Neumann, " The Century's Triumph in Lighting": The Luxfer Prism Companies and Their Contribution to Early Modern Architecture, The Journal of the Society of Architectural Historians 54 (1995) 24-53. https://doi.org/10.2307/991024
- B. Bueno, et al., Fener: A Radiance-based modelling approach to assess the thermal and daylighting performance of complex fenestration systems in office spaces, Energy and Buildings 94 (2015) 10-20. https://doi.org/10.1016/j.enbuild.2015.02.038
- D.M. Kennedy, and F. O'Rourke, Experimental analysis of a scaled, multi-aperture, light-pipe, daylighting system, Solar Energy 122 (2015) 181-190. https://doi.org/10.1016/j.solener.2015.08.013
- E. Lee,and S. Selkowitz, High Performance Building Facade Solutions-PIER Final Project Report, Lawrence Berkeley National Lab.(LBNL), 2009, Berkeley, CA (United States).
- A. Shehabi, et al., US energy savings potential from dynamic daylighting control glazings, Energy and Buildings 66 (2013) 415-423. https://doi.org/10.1016/j.enbuild.2013.07.013
- Y.-C. Chan, and A. Tzempelikos, Daylighting and energy analysis of multi-sectional facades, Energy Procedia 78 (2015) 189-194. https://doi.org/10.1016/j.egypro.2015.11.138
- B. Sourek, et al., Experimental characterization of glazing with glass prisms, Solar Energy 158 (2017) 440-447. https://doi.org/10.1016/j.solener.2017.08.087
- T. Dogan, and P. Stec, Prototyping a façade-mounted, dynamic, dual-axis daylight redirection system, Lighting Research & Technology 50 (2018) 583-595. https://doi.org/10.1177/1477153516675392
- J. Fang, et al., Analysis of dynamic louver control with prism redirecting fenestrations for office daylighting optimization, Energy and Buildings 262 (2022) 112-1s19. https://doi.org/10.1016/j.enbuild.2022.112019
- V. Shemelin, et al. Energy savings potential from prismatic glass structure, in: E3S Web of Conferences, 2020, EDP Sciences. https://doi.org/10.1051/e3sconf/202016706004
- I.A. Mashaly, et al., CFStrace: An evaluation method to include complex fenestration systems in the façade design process, Solar Energy 217 (2021) 253-262. https://doi.org/10.1016/j.solener.2021.01.073
- S.A. Kalogirou, Chapter 2 - Environmental Characteristics, in Solar Energy Engineering,(Second Edition), S.A. Kalogirou, Editor, Boston. 2014. https://doi.org/10.1016/B978-0-12-397270-5.00002-9
- F. Kreith, and J.F. Kreider, Principles of solar engineering. 1978.
- G.B. Arfken, et al., chapter 39 - REFLECTION, REFRACTION, AND GEOMETRIC OPTICS, in University Physics, G.B. Arfken, et al, Editors, Academic Press,1984. https://doi.org/10.1016/B978-0-12-059860-1.50044-8
- R.Kingslake, and B. Johnson, Lens design fundamentals, , academic press, 2009.
Copyright © 2022 The Author(s). Published by solarlits.com.
 HOME
HOME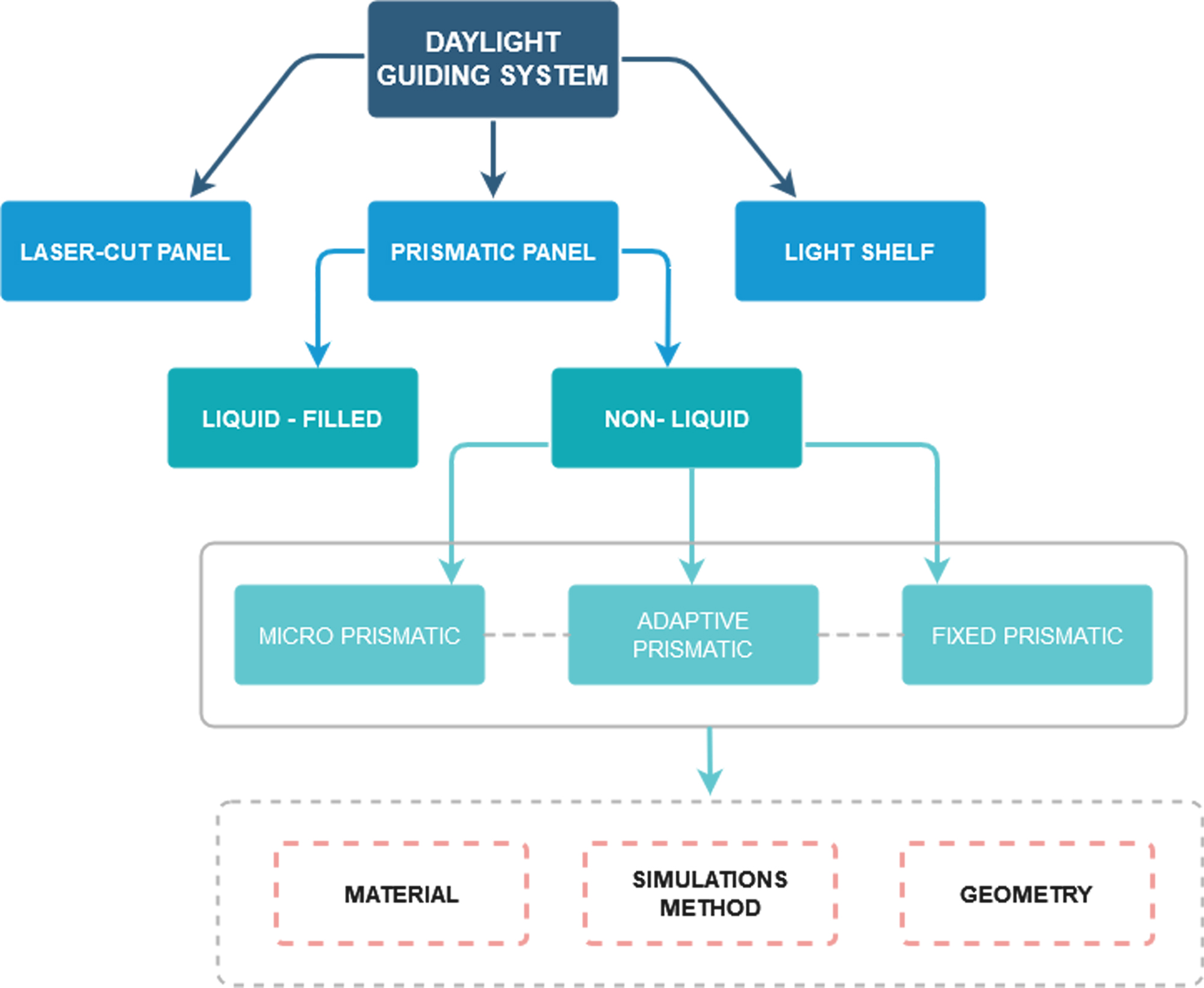 Figure 1
Figure 1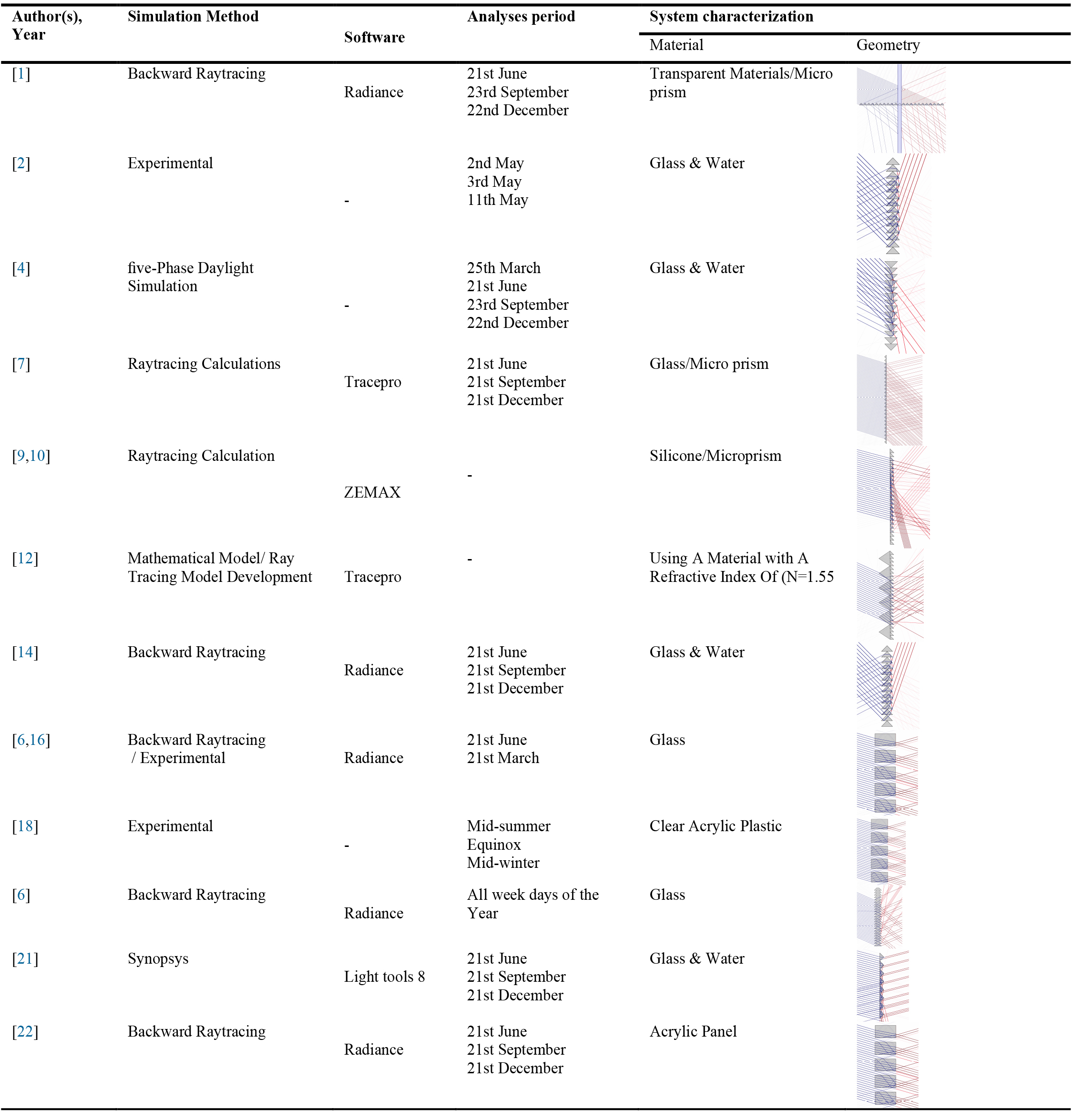 Table 1
Table 1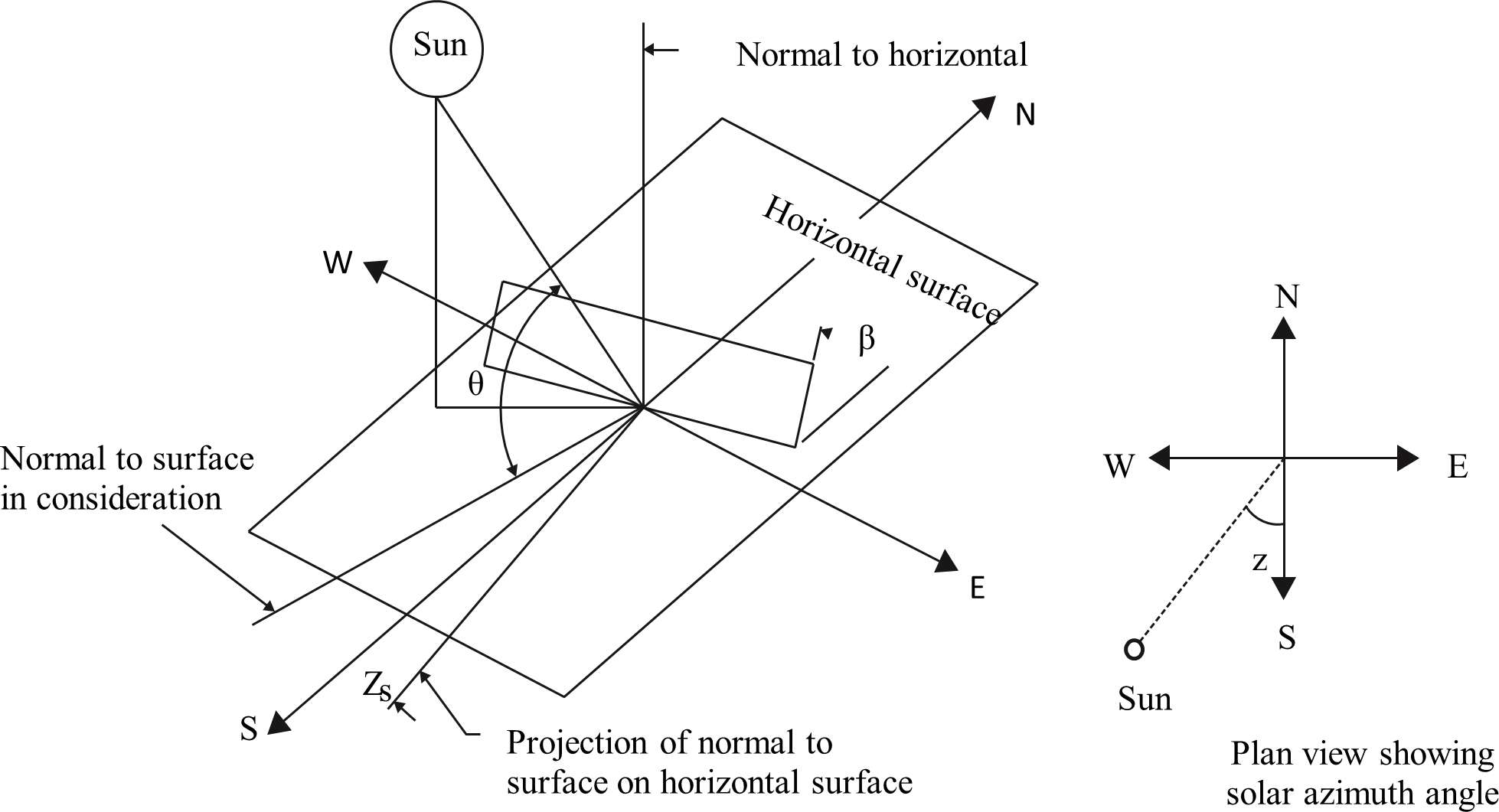 Figure 2
Figure 2 Figure 3
Figure 3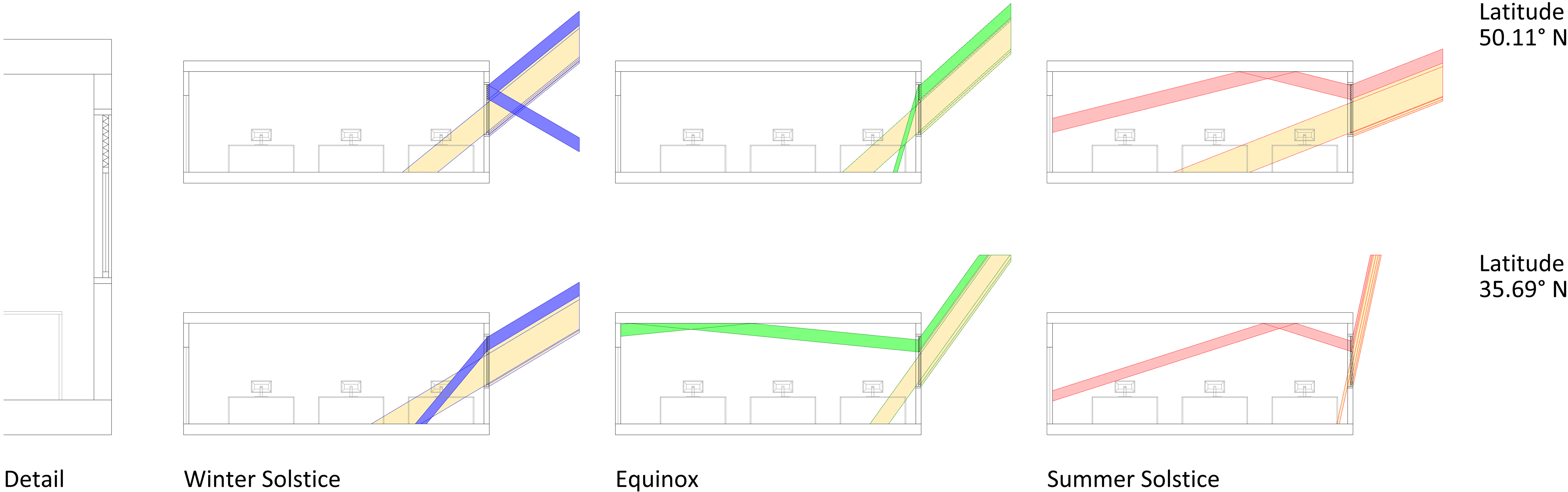 Figure 4
Figure 4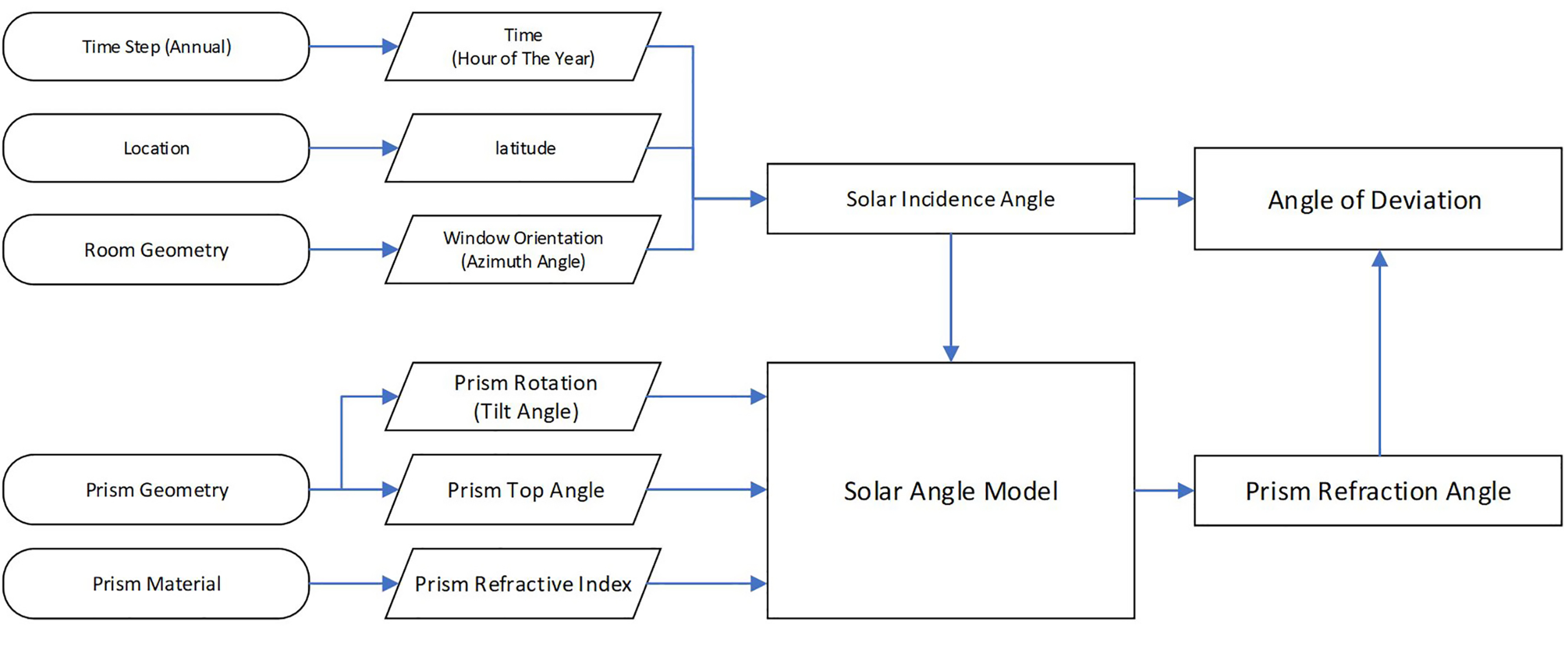 Figure 5
Figure 5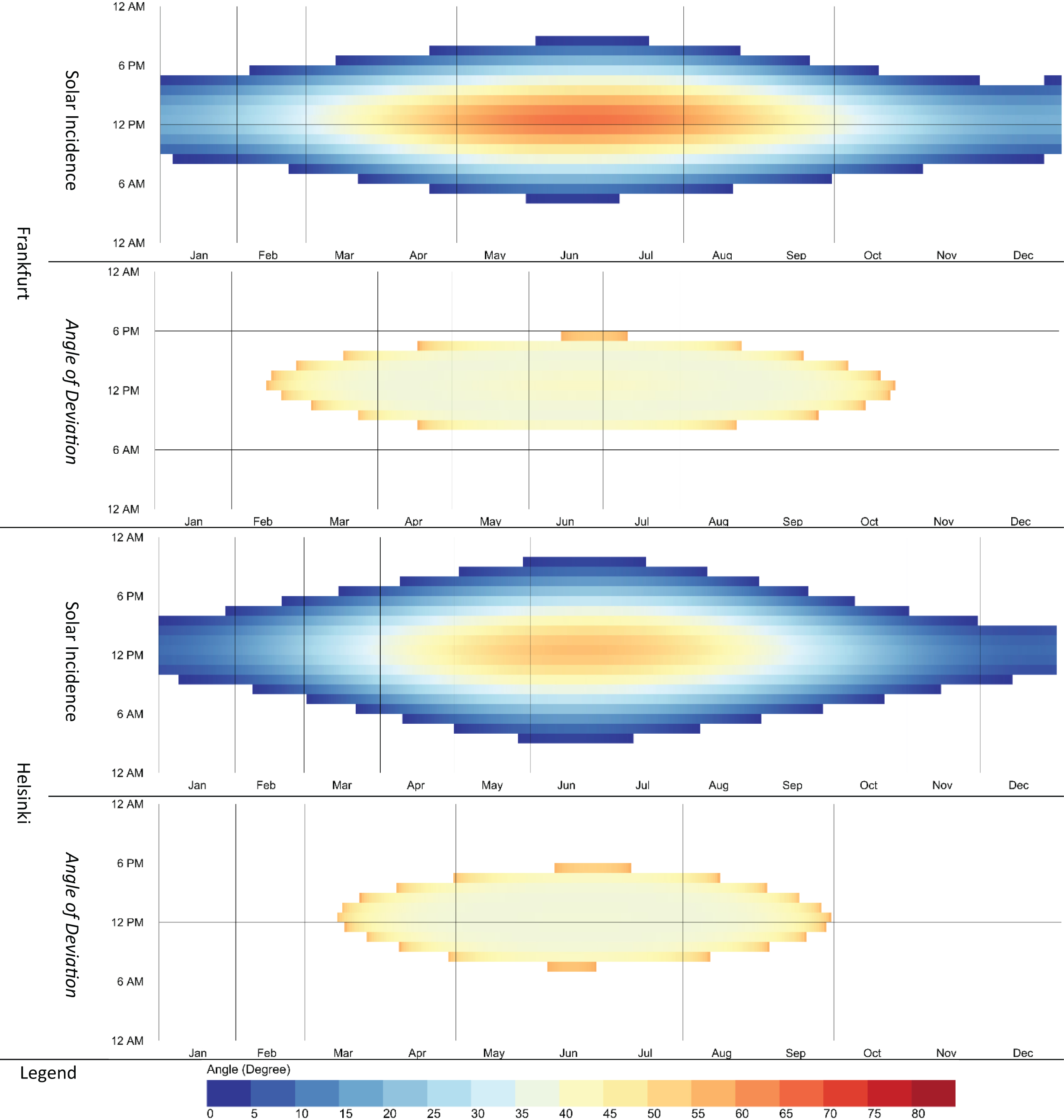 Figure 7
Figure 7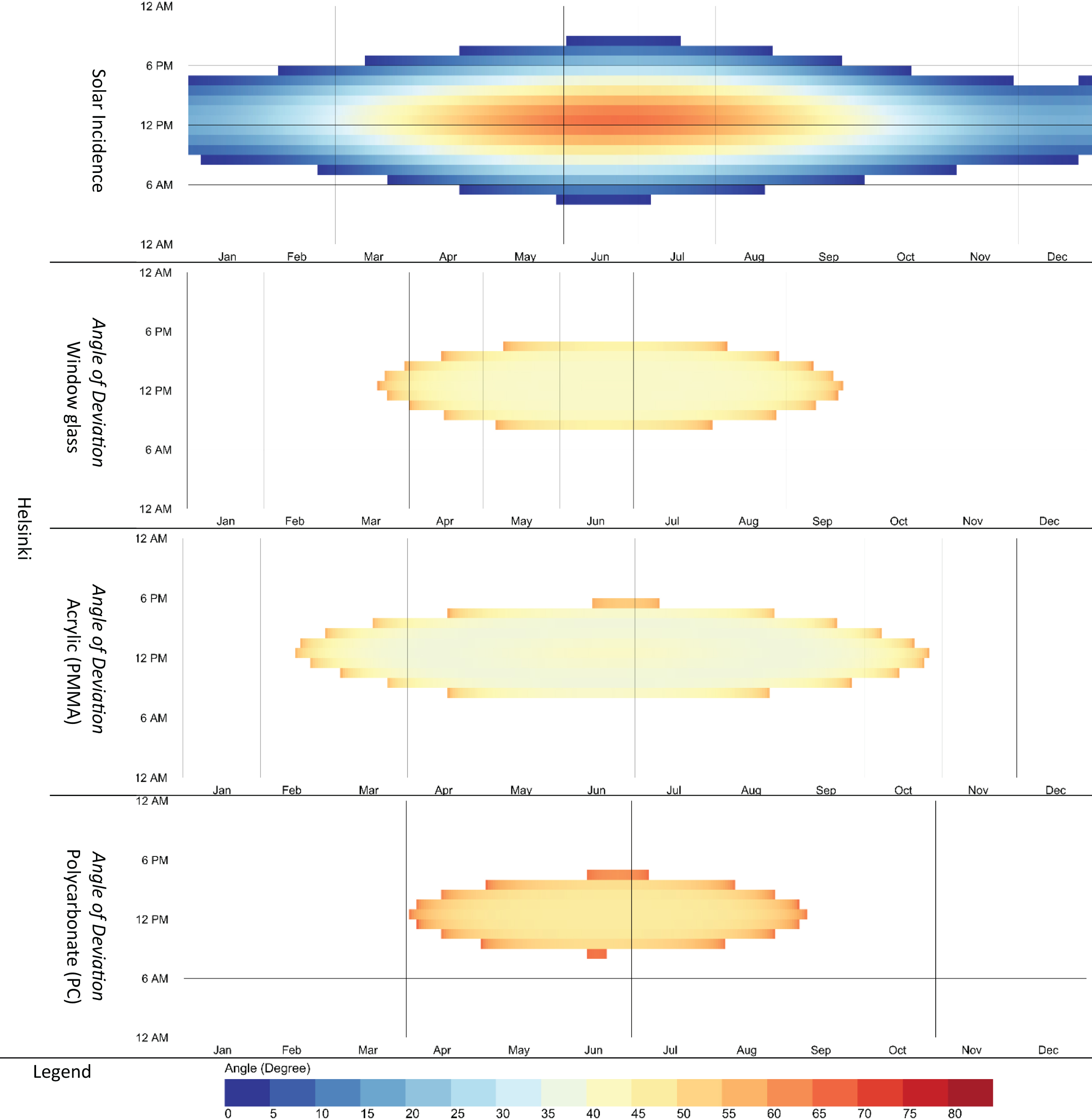 Figure 8
Figure 8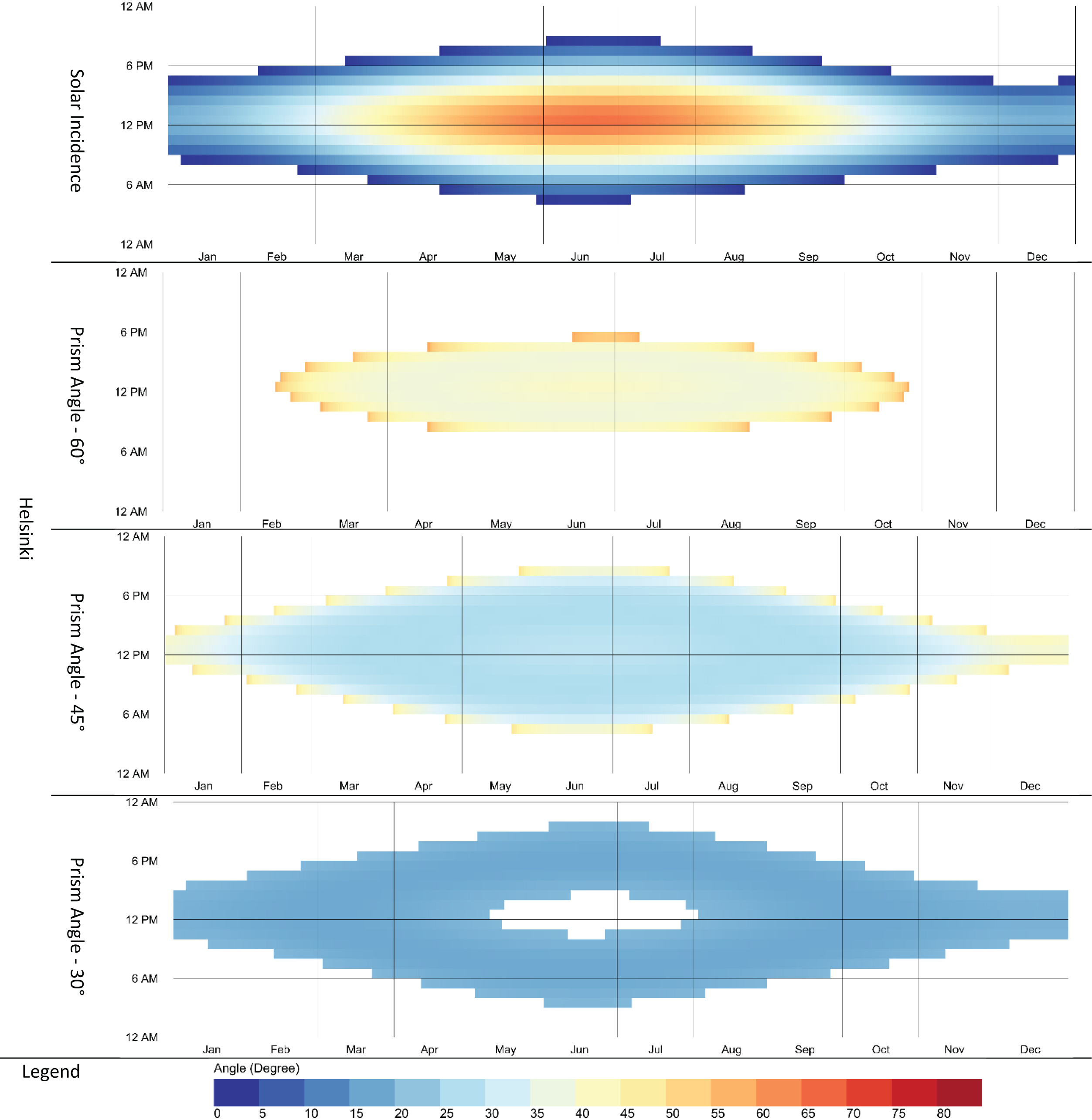 Figure 9
Figure 9